
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальная регрессия. Интервальное оценивание
1. Модель нормальной регрессии. До сих пор делались предположения только о первых и вторых моментах наблюдений [см. условия (5.1) и (5.2) ]. Развитая при этих минимальных предположениях теория наименьших квадратов позволяет получать только точечные оценки для параметров 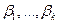 и их линейных комбинаций. Чтобы получать более сильные утверждения (например, оценивать вероятности заданных отклонений о. н. к. от истинных значений рассматриваемых параметров), необходимо сделать дополнительные предположения о виде распределения случайного вектора
и их линейных комбинаций. Чтобы получать более сильные утверждения (например, оценивать вероятности заданных отклонений о. н. к. от истинных значений рассматриваемых параметров), необходимо сделать дополнительные предположения о виде распределения случайного вектора  или, что то же, вектора ошибок
или, что то же, вектора ошибок  , определенного в (5.1). Чаще всего задачи регрессионного анализа решают в предположении, что наблюдения подчиняются нормальному закону распределения; в этом случае к условиям (5.1) и (5.2) добавляют третье условие
, определенного в (5.1). Чаще всего задачи регрессионного анализа решают в предположении, что наблюдения подчиняются нормальному закону распределения; в этом случае к условиям (5.1) и (5.2) добавляют третье условие
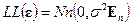 . (5.39)
. (5.39)
Если выполнены условия (5.1) и (5.39) [условие (5.2) вытекает из (5.39)], то говорят о нормальной регрессии.
Отметим, что условия (5.1) и (5.39) можно объединить и записать в виде
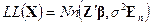 (5.40)
(5.40)
2. Оценки максимального правдоподобия параметров нормальной регрессии. Нормальная модель (5.40) определяется 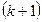 -мерным параметром
-мерным параметром  , область возможных значений которого представляет собой евклидово полупространство
, область возможных значений которого представляет собой евклидово полупространство 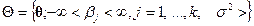 . Если
. Если  — наблюдавшаяся реализация вектора
— наблюдавшаяся реализация вектора 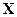 , то функция правдоподобия для этой модели имеет вид
, то функция правдоподобия для этой модели имеет вид
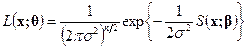 ,
,
где квадратичная форма 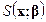 определена в (5.4).
определена в (5.4).
Вычислим оценки параметров 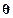 с помощью метода максимального правдоподобия (см. § 2.4). Из (5.41) имеем, что при любом
с помощью метода максимального правдоподобия (см. § 2.4). Из (5.41) имеем, что при любом 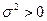 максимизация
максимизация 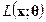 по
по 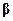 эквивалентна минимизации по
эквивалентна минимизации по 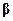 квадратичной формы
квадратичной формы 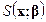 . Таким образом, для нормальной модели оценки наименьших квадратов коэффициентов регрессии
. Таким образом, для нормальной модели оценки наименьших квадратов коэффициентов регрессии 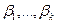 совпадают с оценками максимального правдоподобия этих параметров.
совпадают с оценками максимального правдоподобия этих параметров.
Из теоремы 5,2 следует, что о.н.к. являются оптимальными в классе линейных оценок. Для схемы нормальной регрессии справедливо более сильное утверждение: о.н.к. являются оптимальными в классе всех (не только линейных) несмещенных оценок рассматриваемых параметрических функций.
Найдем оценку максимального правдоподобия  для остаточной дисперсии
для остаточной дисперсии 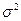 . Подставив в (5.41) вместо
. Подставив в (5.41) вместо 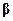 оценку
оценку 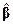 и прологарифмировав, находим, что
и прологарифмировав, находим, что  —это то значение
—это то значение 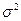 , которое минимизирует выражение
, которое минимизирует выражение 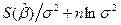 . Отсюда имеем
. Отсюда имеем
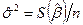 . (5-42)
. (5-42)
Но, как было показано [см. (5.141], в общем случае несмещенная оценка для 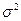 имеет вид
имеет вид  , поэтому о. м. п.
, поэтому о. м. п.  оказывается смещенной и ее смещение
оказывается смещенной и ее смещение
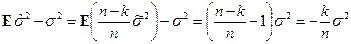
убывает по модулю с ростом числа наблюдений  . Таким образом, оценка (5.42) является асимптотически несмещенной (что характерно для о. м. п.).
. Таким образом, оценка (5.42) является асимптотически несмещенной (что характерно для о. м. п.).
3. Основная теорема. Докажем следующую важную теорему теории нормальной регрессии, которая будет неоднократно использоваться в дальнейшем.
Теорема 5.4. Случайные величины 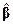 и
и  , а также
, а также 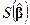 и
и 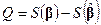 независимы; при этом
независимы; при этом
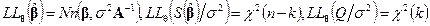 . (5.43)
. (5.43)
□ Введем нормированный вектор ошибок  ; тогда равенство (5.1) принимает вид
; тогда равенство (5.1) принимает вид
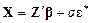 , (5,44)
, (5,44)
а равенство (5.6) — следующий вид:
 . (5.45)
. (5.45)
Подставив вместо 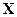 его выражение (5.44) в (5.16), получим
его выражение (5.44) в (5.16), получим
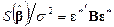 , (5.46)
, (5.46)
поскольку 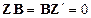 [матрица
[матрица 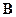 определена в (5.15)]. Наконец, из тождества (5.8) имеем следующее представление для
определена в (5.15)]. Наконец, из тождества (5.8) имеем следующее представление для 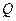 :
:
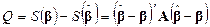 . (5.47)
. (5.47)
Независимость 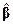 и
и  следует из представлений (5.45) и (5.46), легко устанавливаемого факта
следует из представлений (5.45) и (5.46), легко устанавливаемого факта 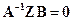 и леммы 1.2.
и леммы 1.2.
Далее, из представления (5.47) имеем, что случайная величина 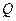 зависит от выборки
зависит от выборки 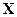 лишь через
лишь через 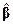 ; следовательно, в силу независимости
; следовательно, в силу независимости 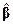 и
и  случайные величины
случайные величины 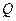 и
и  также независимы. Первая часть теоремы доказана.
также независимы. Первая часть теоремы доказана.
Докажем теперь утверждения (5.43) о распределениях рассматриваемых случайных величин. Так как 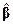 —линейная функция нормального вектора [см. представление (5.45)], то закон распределения
—линейная функция нормального вектора [см. представление (5.45)], то закон распределения 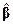 также нормален. Первые и вторые моменты вектора
также нормален. Первые и вторые моменты вектора 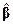 вычислены в п. 2 § 5.2.
вычислены в п. 2 § 5.2.
Закон распределения  устанавливается на основа представления (5.47), факта нормальности вектора
устанавливается на основа представления (5.47), факта нормальности вектора 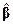 и теоремы 1.9. Наконец, закон распределения
и теоремы 1.9. Наконец, закон распределения 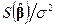 устанавливается на основании представления (5.46) и леммы 1.4, поскольку
устанавливается на основании представления (5.46) и леммы 1.4, поскольку
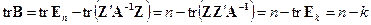
Следствие 1. Из первого соотношения в (5.43) имеем, что для любого 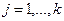
 (5.48)
(5.48)
и  ; не зависит от
; не зависит от  . Поэтому из определения распределения Стьюдента (см. п. 4 § 1.5) и из теоремы 5.4 следует, что при любом
. Поэтому из определения распределения Стьюдента (см. п. 4 § 1.5) и из теоремы 5.4 следует, что при любом 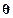
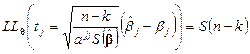 (5.49)
(5.49)
Следствие 2. Из определения распределения Снедекора (см. п. 5 § 1.5) и теоремы 5.4 имеем, что при любом 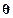
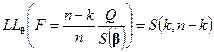 .
.
4. Доверительное оценивание параметров нормальной регрессии. Найдем доверительный интервал для коэффициента регрессии 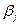 . Из соотношения (5.48) следует, что статистика
. Из соотношения (5.48) следует, что статистика 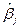 имеет распределение
имеет распределение  . Следовательно, имеет место задача оценивания неизвестного среднего нормального закона с неизвестной дисперсией (так как
. Следовательно, имеет место задача оценивания неизвестного среднего нормального закона с неизвестной дисперсией (так как 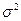 неизвестно) по наблюдению над случайной величиной
неизвестно) по наблюдению над случайной величиной 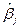 . На основании (5.49) стьюдентово отношение
. На основании (5.49) стьюдентово отношение 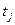 является центральной статистикой для оценивания
является центральной статистикой для оценивания 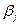 (см. п. 2 § 2.6), поэтому
(см. п. 2 § 2.6), поэтому 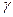 -доверительный интервал для
-доверительный интервал для 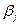 , строится по схеме примера 2.30 и имеет вид
, строится по схеме примера 2.30 и имеет вид
 (5.51)
(5.51)
Это симметричный интервал относительно точки 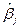 , длины
, длины

Чтобы построить доверительный интервал для остаточной дисперсии 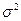 , воспользуемся вторым из соотношений (5.43), из которого следует, что
, воспользуемся вторым из соотношений (5.43), из которого следует, что 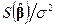 — нужная центральная статистика. Искомый
— нужная центральная статистика. Искомый 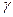 -доверительный интервал строится здесь по схеме примера 2.30 и имеет вид
-доверительный интервал строится здесь по схеме примера 2.30 и имеет вид
 (5.52)
(5.52)
Итак, можно построить доверительный интервал для каждого из коэффициентов регрессии 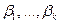 . Если построить
. Если построить 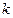 таких интервалов с одним и тем же уровнем
таких интервалов с одним и тем же уровнем 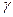 , то среднее значение числа интервалов, накрывающих соответствующие значения
, то среднее значение числа интервалов, накрывающих соответствующие значения 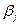 , равно
, равно 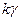 . Оценим вероятность одновременного накрытия построенными интервалами соответствующих параметров.
. Оценим вероятность одновременного накрытия построенными интервалами соответствующих параметров.
Обозначим через  событие, состоящее в том, что интервал (5.51), в котором
событие, состоящее в том, что интервал (5.51), в котором 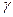 заменено на
заменено на  , накрывает параметр
, накрывает параметр 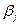 , т.е.
, т.е. 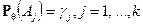 . Тогда вероятность совместного осуществления событий
. Тогда вероятность совместного осуществления событий  можно записать так:
можно записать так:
 . Но
. Но
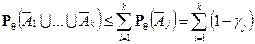
[*] C. Radhakrishna Rao. Methodology based on the  -norm, in statistical interence.- Sankhya, A, 1988. V.50. № 3. P. 289 - 313.
-norm, in statistical interence.- Sankhya, A, 1988. V.50. № 3. P. 289 - 313.
|
|
Дата добавления: 2015-05-09; Просмотров: 784; Нарушение авторских прав?; Мы поможем в написании вашей работы!