
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценивание неизвестных параметров модели 2 страница
|
|
|
|
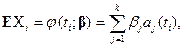
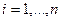 (5.29)
(5.29)
Определенная здесь функция 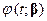 представляет собой полином (параболу) степени
представляет собой полином (параболу) степени 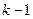 и называется кривой параболической регрессии.
и называется кривой параболической регрессии.
Приведем типичную ситуацию, когда имеет место схема параболической регрессии. Предположим, что имеется теоретическая зависимость вида 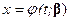 между переменными
между переменными 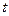 и
и 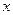 , причем значения
, причем значения 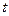 и
и 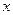 получают из наблюдений. Задача состоит в определении по экспериментальным данным неизвестных параметров
получают из наблюдений. Задача состоит в определении по экспериментальным данным неизвестных параметров 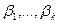 входящих в это уравнение. Каждое измерение
входящих в это уравнение. Каждое измерение 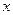 при заданном
при заданном 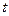 дает уравнение, связывающее неизвестные параметры, и если бы измерения величины
дает уравнение, связывающее неизвестные параметры, и если бы измерения величины 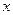 производились без погрешностей, то для определения параметров
производились без погрешностей, то для определения параметров 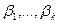 было бы достаточно
было бы достаточно 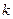 измерений. Однако точные измерения на практике чаще всего невозможны, поэтому для заданных значений
измерений. Однако точные измерения на практике чаще всего невозможны, поэтому для заданных значений 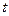 соответствующие значения
соответствующие значения 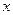 известны с какими-то погрешностями, т. е. реально вместо точного значения
известны с какими-то погрешностями, т. е. реально вместо точного значения 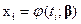 имеем случайный результат
имеем случайный результат 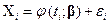 , где
, где 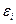 — ошибка измерения. Если условия эксперимента обеспечивают отсутствие систематической ошибки (
— ошибка измерения. Если условия эксперимента обеспечивают отсутствие систематической ошибки (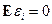 ), равноточность (
), равноточность (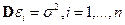 ) и некоррелированность (
) и некоррелированность (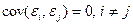 ) результатов измерений, то приходим к схеме регрессии вида (5.29).
) результатов измерений, то приходим к схеме регрессии вида (5.29).
Чтобы исключить влияние погрешностей измерений, нужна дополнительная информация. Для этого производят большое число измерений 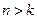 . Полученные экспериментальные данные обрабатывают по методу наименьших квадратов. В результате
. Полученные экспериментальные данные обрабатывают по методу наименьших квадратов. В результате
 находят не точные значения коэффициент
находят не точные значения коэффициент 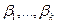 , а определяют их о. п. к.
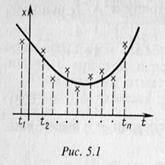
, а определяют их о. п. к. 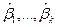 . В данном случае этому метод можно дать следующую наглядную геометрическую интерпретацию (рис. 5.1).
. В данном случае этому метод можно дать следующую наглядную геометрическую интерпретацию (рис. 5.1).
Нанесем на плоскости 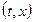 наблюдавшиеся точки
наблюдавшиеся точки 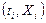 ,
, 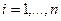 . Тогда значения
. Тогда значения 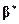 неизвестных коэффициентов
неизвестных коэффициентов 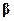 подбирают так, чтобы соответствующий эмпирический график
подбирают так, чтобы соответствующий эмпирический график 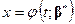 наилучшим образом проходил около наблюдавшихся точек. Если в качестве критерия оптимальности взять величину
наилучшим образом проходил около наблюдавшихся точек. Если в качестве критерия оптимальности взять величину 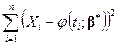 , то приходим к методу наименьших квадратов с решением
, то приходим к методу наименьших квадратов с решением 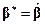 .
.
Формально такой же вид имеет и классическая задача математического анализа приближения функций многочленами. В этом случае данные 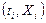 ,
, 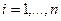 , интерпретируют как пары соответствующих абсцисс и ординат графика изучаемой функции и задача состоит в подборе и нтерполяционного многочлена вида
, интерпретируют как пары соответствующих абсцисс и ординат графика изучаемой функции и задача состоит в подборе и нтерполяционного многочлена вида 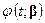 , который давал бы наилучшее приближение в среднем, т.е. минимизировал бы величину
, который давал бы наилучшее приближение в среднем, т.е. минимизировал бы величину 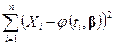 .
.
7. Ортогональные многочлены Чебышева. В описанной в примере 5.2 схеме предполагалось, что многочлены 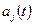 известны. В частном случае
известны. В частном случае 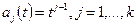 ; тогда
; тогда 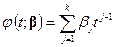 , т. е.
, т. е. 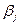 с коэффициенты многочлена
с коэффициенты многочлена 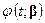 (это имеет место в примере 5.1). В других случаях (что особенно характерно для задач интерполяции) многочлены
(это имеет место в примере 5.1). В других случаях (что особенно характерно для задач интерполяции) многочлены 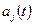 можно выбрать достаточно произвольно; их следует взять такими, чтобы можно было упростить дальнейшие вычисления. Наиболее просто решается задача вычисления о. п. к.
можно выбрать достаточно произвольно; их следует взять такими, чтобы можно было упростить дальнейшие вычисления. Наиболее просто решается задача вычисления о. п. к. 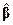 при диагональной матрице
при диагональной матрице 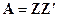 . В этом случае [см. (5.25)]
. В этом случае [см. (5.25)]
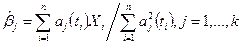 . (5.30)
. (5.30)
Условием диагональности матрицы 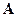 является ортогональность векторов
является ортогональность векторов 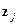 :
:
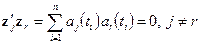 (5.31)
(5.31)
Многочлены, удовлетворяющие условиям (5.31), называют ортогональными многочленами Чебышева.
Покажем, что при заданных 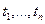 , такие многочлены всегда можно построить. Без потери общности будем предполагать старший коэффициент
, такие многочлены всегда можно построить. Без потери общности будем предполагать старший коэффициент 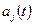 равным единице, т.е.
равным единице, т.е. 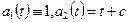 , … Из условия (5.31) при
, … Из условия (5.31) при 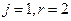 имеем
имеем
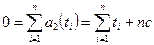 ,
,
т.е. 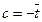 . Таким образом,
. Таким образом, 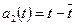 .
.
Выведем рекуррентную формулу, позволяющую вычислять следующий многочлен по двум предыдущим — этим и доказывается существование всех многочленов 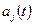 . Предположим, что для некоторого
. Предположим, что для некоторого 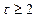 многочлены
многочлены 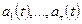 уже построены. Рассмотрим произвольный многочлен
уже построены. Рассмотрим произвольный многочлен 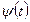 степени
степени 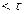 . Его можно однозначно выразить в виде линейной комбинации многочленов
. Его можно однозначно выразить в виде линейной комбинации многочленов 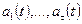 :
: 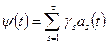 . Действительно, из условия ортого- нальности (5.31) при
. Действительно, из условия ортого- нальности (5.31) при 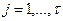 имеем
имеем
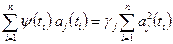 ,
,
т. е. эти равенства однозначно определяют коэффициенты 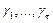 . Отсюда, в частности, следует, что если
. Отсюда, в частности, следует, что если 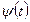 — многочлен степени
— многочлен степени 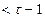 , то
, то
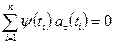 . (5.32)
. (5.32)
Рассмотрим теперь многочлен степени 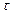 следующего вида:
следующего вида:
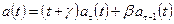 (5.33)
(5.33)
(старший коэффициент здесь равен 1). Если 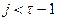 . то в силу (5.32)
. то в силу (5.32)

(так как степень многочлена  равна
равна 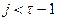 ), т.е. при любых постоянных
), т.е. при любых постоянных 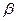 и
и 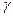 многочлен (5.33) ортогонален всем многочленам
многочлен (5.33) ортогонален всем многочленам 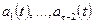 . Выберем эти постоянные так, чтобы многочлен (5.33) был ортогонален также
. Выберем эти постоянные так, чтобы многочлен (5.33) был ортогонален также 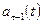 и
и 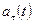 . Для этого должны выполняться следующие условия:
. Для этого должны выполняться следующие условия:
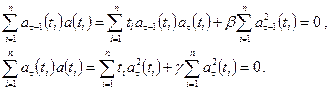
Отсюда
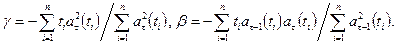 (5.34)
(5.34)
При таком выборе постоянных 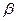 и
и 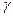 многочлен (5.33) ортогонален всем многочленам
многочлен (5.33) ортогонален всем многочленам 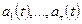 и, следовательно, является следующим многочленом
и, следовательно, является следующим многочленом 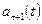 системы Чебышева. Таким образом, приведен алгоритм построения системы ортогональных многочленов Чебышева. Первых два многочлена этой системы указаны выше; в частности, из (5.33) и (5.34) имеем общий третьего многочлена
системы Чебышева. Таким образом, приведен алгоритм построения системы ортогональных многочленов Чебышева. Первых два многочлена этой системы указаны выше; в частности, из (5.33) и (5.34) имеем общий третьего многочлена
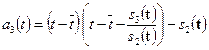 , (5.35)
, (5.35)
где 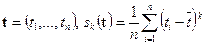 .
.
Итак, если в схеме параболической регрессии (5.29) многочлены 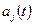 являются ортогональными многочленами Чебышева, то о. н. к.
являются ортогональными многочленами Чебышева, то о. н. к. 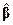 вычисляют по формулам (5.30), а соответствующее значение
вычисляют по формулам (5.30), а соответствующее значение 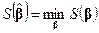 таково:
таково:
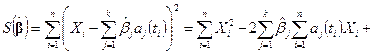
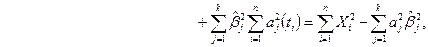 (5.36)
(5.36)
где 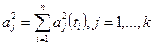 .
.
Отметим следующее важное обстоятельство. Как видно из формулы (5.30), о. н. к. 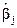 определяется только многочленом
определяется только многочленом 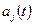 и не зависит от параметра
и не зависит от параметра 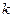 схемы (5.29). Это позволяет упростить задачу построения интерполяционного многочлена более высокой степени, если требуется повысить точность интерполяции. Так, предположим, что для заданного
схемы (5.29). Это позволяет упростить задачу построения интерполяционного многочлена более высокой степени, если требуется повысить точность интерполяции. Так, предположим, что для заданного 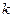 построен интерполяционный многочлен
построен интерполяционный многочлен 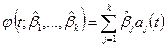 , однако значение
, однако значение 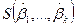 [см. соотношение (5.36)] еще велико, что означает недостаточную точность приближения исследуемой функции многочленом степени
[см. соотношение (5.36)] еще велико, что означает недостаточную точность приближения исследуемой функции многочленом степени 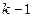 . Точность интерполяции можно повысить, приближая функцию многочленом степени
. Точность интерполяции можно повысить, приближая функцию многочленом степени 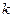 вида
вида
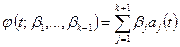
т.е. добавляя следующий, 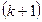 -й многочлен системы Чебышева. При нахождении такого оптимального многочлена оценки коэффициентов
-й многочлен системы Чебышева. При нахождении такого оптимального многочлена оценки коэффициентов 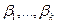 остаются теми же
остаются теми же 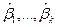 , необходимо вычислить только
, необходимо вычислить только 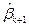 по формуле (5.30). Далее имеем
по формуле (5.30). Далее имеем
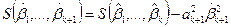 , (5.37)
, (5.37)
и если точность приближения, достигнутая с помощью многочлена 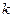 -й степени, недостаточна, то можно подбирать далее многочлен
-й степени, недостаточна, то можно подбирать далее многочлен 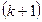 -й степени и т. д.
-й степени и т. д.
Пример 5.3. В «Основах химии» Д. И. Менделеев приводит следующие данные о количестве 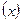 азотно-натриевой соли NaNOз, которое можно растворить в 100 г воды в зависимости температуры
азотно-натриевой соли NaNOз, которое можно растворить в 100 г воды в зависимости температуры 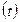 ;
;
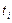
| |||||||||
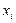
| 66,7 | 71,0 | 76,3 | 80,6 | 85,7 | 92,9 | 99,4 | 113,6 | 125,1 |
Построим по этим данным приближенную эмпирическую формулу вида 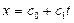 , описывающую зависимость между рассматриваемыми величинами. Здесь имеет место линейная зависимость, поэтому это схема простой регрессии, рассмотренная в примере 5.1. Используя формулы (5.27), получаем:
, описывающую зависимость между рассматриваемыми величинами. Здесь имеет место линейная зависимость, поэтому это схема простой регрессии, рассмотренная в примере 5.1. Используя формулы (5.27), получаем:  ,
, 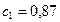 . Таким образом, искомая приближенная формула имеет вид
. Таким образом, искомая приближенная формула имеет вид
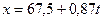 .
.
При этом сумма квадратов отклонений, вычисленная по формуле (5.28), равна 11,1.
Установим, как повышается точность приближения, если в качестве интерполяционного многочлена использовать квадратичную параболу. Запишем искомый многочлен в виде
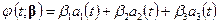 ,
,
где 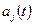 — многочлен Чебышева [здесь
— многочлен Чебышева [здесь 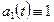 ,
, 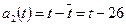 , многочлен
, многочлен 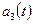 определен в (5.35)]. Результат (5.38) можно записать в виде
определен в (5.35)]. Результат (5.38) можно записать в виде 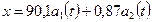 , следовательно,
, следовательно, 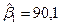 ,
, 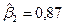 . Таким образом, достаточно вычислить по формуле (5.30)
. Таким образом, достаточно вычислить по формуле (5.30) 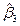 . В данном случае
. В данном случае 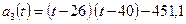 , поэтому значения
, поэтому значения 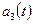 в точках
в точках 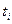 - таковы: 588,9; 340,9; 28,9; -176,1: -356,1; -484,1; -491,1; -176,1; 724,9. Отсюда
- таковы: 588,9; 340,9; 28,9; -176,1: -356,1; -484,1; -491,1; -176,1; 724,9. Отсюда 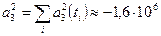 ,
, 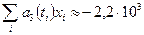 и по формуле (5.30)
и по формуле (5.30) 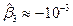 ; поправка в (5.37)
; поправка в (5.37) 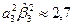 .
.
Таким образом, учитывая многочлен второй степени, мы незначительно увеличиваем точность аппроксимации данных; в качестве удовлетворительной эмпирической зависимости можно принять формулу (5.38).
В заключение сделаем следующее общее замечание. В основе изложенного в этом параграфе классического метода наименьших квадратов лежит минимизация (по 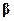 ) выражения
) выражения 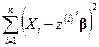 . Альтернативным к этому методу оценивания параметров регрессии является метод, основанный на минимизации выражения
. Альтернативным к этому методу оценивания параметров регрессии является метод, основанный на минимизации выражения 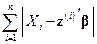 , т.е. суммы абсолютных уклонений наблюдений от их математических ожиданий. Оценки параметров
, т.е. суммы абсолютных уклонений наблюдений от их математических ожиданий. Оценки параметров 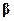 , получаемые этим методом, называются оценками найменьших модулей. В последнее время повысился интерес к этому методу, так как оценки наименьших модулей, как оказалось, обладают рядом интересных (с позиций приложений) свойств; в частности, они являются более устойчивыми по отношениюи к аномальным наблюдениям (в современной терминологии — более робастными).[*]
, получаемые этим методом, называются оценками найменьших модулей. В последнее время повысился интерес к этому методу, так как оценки наименьших модулей, как оказалось, обладают рядом интересных (с позиций приложений) свойств; в частности, они являются более устойчивыми по отношениюи к аномальным наблюдениям (в современной терминологии — более робастными).[*]
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 401; Нарушение авторских прав?; Мы поможем в написании вашей работы!