Двоичные счетчики

Наиболее удобным базовым элементом для построения счетчиков является счетный триггер Т-типа. Такой триггер по сути является простейшим счетчиком с . Соединив несколько Т-триггеров определенным образом в последовательную структуру, можно получить схему многоразрядного счетчика. Если в качестве базовых используются Т-триггеры с прямым динамическим счетным входом, то для построения трехразрядного суммирующего двоичного счетчика их необходимо объединить так, как это показано на рис. 9.15, а. Поскольку срабатывание всех триггеров с прямым динамическим счетным входом происходит по переднему фронту счетного импульса, то для реализации операции суммирования необходимо на триггеры Т2 и Т3 информацию подавать с инверсных выходов 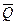предыдущих триггеров. Временная диаграмма работы триггеров в такой счетной схеме показана на рис.9.15, б (крестиком на импульсах показано срабатывание по переднему фронту). Состояния выходов Q ₁, Q ₂ и Q ₃ сгруппируем в зависимости от номера счетного импульса в таблице 9.7. Из рисунка и таблицы очевидно, что двоичный код, задаваемый логическими состояниями выходов счетчика соответствует порядковому номеру входного счетного импульса С. При подаче последнего восьмого импульса счетчик возвращается в исходное состояние, после чего процесс повторяется. Модуль счета в такой схеме будет равен К_сч =2³=8. Условное графическое обозначение двоичного трехразрядного счетчика с весовыми обозначениями выходов показано на рис. 9.15, в.

Рис. 9.15. Схема трехразрядного двоичного суммирующего счетчика на основе Т-триггеров с прямым динамическим счетным входом (а), его временная диаграмма (б) и УГО (в).

Таблица 9.7.

Номер счетного импульса	Исходное состояние
Q 1
Q 2
Q 3
Десятичный код

Суммирующий счетчик можно построить и на базе Т-триггеров с инверсным динамическим счетным входом. При этом, поскольку срабатывание триггеров происходит по заднему фронту счетного импульса, нет необходимости задействовать инверсные выходы 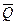этих триггеров. Сигнал на вход каждого последующего триггера необходимо подавать с прямого выхода предыдущего триггера (рис. 9.16, а). При этом необходимо учитывать, что срабатывание всего счетчика будет происходить по заднему фронту счетного импульса С, как это показано на временной диаграмме рис. 9.16, б.

Рис. 9.16. Схема трехразрядного двоичного суммирующего счетчика на основе Т-триггеров с инверсным динамическим счетным входом (а) и его временная диаграмма (б).

Для выполнения операции вычитания достаточно изменить в электрических связях соответствующих схем используемые выходы триггеров на выходы с обратными логическими уровнями, либо использовать триггеры с входами обратного типа динамического управления. Если вычитающий счетчик реализуется на базе Т-триггеров с прямым динамическим входом, то сигналы на входы последующих триггеров необходимо подавать с прямых выходов предыдущих триггеров (рис. 9.17, а). Временная диаграмма работы счетчика, псотренного по такой схеме, приведена на рис. 9.17, б. Из временной диаграммы видно, что с каждым последующим счетным импульсом выходной код уменьшается на единицу (декрементируется). С последним восьмым импульсом счетчик возвращается в исходное нулевое состояние.

Рис. 9.17. Схема трехразрядного двоичного вычитающего счетчика на основе Т-триггеров с прямым динамическим счетным входом (а) и его временная диаграмма (б).

Таким образом, путем переключения выходов с инверсных на не инверсные и обратно, можно получить как суммирующие, так и вычитающие счетчики. Это свойство положено в основу построения реверсных счетчиков. Коммутацию прямых или инверсных выходов триггеров предыдущих разрядов на входы триггеров последующих разрядов удобно выполнять с помощью элементов 2И-ИЛИ или 2И-ИЛИ-НЕ. На схеме рис. 9.18 показан пример реализации трехразрядного реверсивного счетчика на основе T-триггеров с прямым динамическим счетным входом и элементов 2И-ИЛИ-НЕ в качестве комуутаторов. При логическом нуле на линии «-1» и логической единице на линии «+1», на выходе верхней структуры И элементов ЛЭ1 и ЛЭ2 формируется результат с выходов Q ₁ и Q ₂ соответствующих триггеров. На выходе нижней структуры И присутствует логический нуль, в результате чего выходы 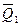и 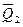не влияют на работу схемы. Структура ИЛИ-НЕ элементов ЛЭ1 и ЛЭ2 инвертирует значения соответствующих коммутируемых выходов. Таким образом, осуществляется инверсия сигналов Q ₁ и Q ₂, которые подаются на прямые динамические входы триггеров Т2 и Т3. Счетчик работает в режиме суммирования. При логическом нуле на линии «+1» и логической единице на линии «-1» режим меняется. Закрытыми оказываются прямые выходы Q ₁, Q ₂, а открываются инверсные выходы 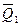и 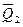. При этом их значения инвертируются элементами ИЛИ-НЕ ЛЭ1 и ЛЭ2, в результате чего они становятся прямыми. Счетчик начинает работать в режиме вычитания. С целью упрощения процесса управления направлением счета сигналы «+1» и «-1» часто формируют с помощью RS-триггера. Эти сигналы запоминаются RS-триггером путем установки его в ноль или единицу сигналами управления «Инк» (инкремент) и «Дек» (декремент). Часто в схемах реверсивного счетчика для указания направления счета используется один вход. В этом случае RS-триггер в схеме отсутствет, а одна из линий выбора направления счета, например «+1», выводится непосредственно как внешний вывод. Сигнал второй линии «-1» формируется через инвертор. Изображенный на рис.9.18 счетчик называется одноканальным, поскольку он имеет один счетный вход C как для режима суммирования, так и для режима вычитания.

Рис. 9.18. Схема трехразрядного одноканального двоичного реверсивного счетчика.

В рассмотренных счетчиках срабатывание триггеров происходит поочередно друг за другом, т.е. последовательно. Такие счетчики также называются асинхронными. Их недостаток состоит в том, что увеличивается общее время установления t_уст с увеличением числа триггеров. Кроме того, появление промежуточных комбинаций может привести к ложному срабатыванию следующего устройства, подключенного к счетчику. Между тем, из таблицы 9.7 видно, что если значение младшего разряда меняется каждый раз с приходом счетного импульса, то в остальных разрядах значения будут меняться на противоположные только в тех случаях, когда в предшествующем состоянии выходного кода во всех предыдущих разрядах были единицы. Указанное правило положено в основу работы синхронных счетчиков. Идея синхронного счетчика заключается в построении внешней комбинационной схемы, формирующей сигналы, согласно которым будет происходить одновременное переключение только части триггеров в зависимости от текущего выходного кода. Причем эти сигналы должны быть сформированы до поступления очередного счетного импульса. Счетный импульс должен поступать на все триггеры одновременно. Для реализации такого счетчика можно использовать как тактируемые Т-триггеры, так и асинхронные.

Пример построения синхронного счетчика на базе тактируемых T-триггеров приведен на рис. 9.19, а. В схеме синхронного счетчика Т-триггер текущего разряда должен включиться в счетный режим и поменять свое состояние на противоположное с приходом каждого тактового импульса только в том случае, если выходы всех триггеров предыдущих разрядов установлены в единицу. Для этих целей необходимо использовать схему совпадения единиц, т.е. вентили И (ЛЭ1 и ЛЭ2). Срабатывание всех триггеров происходит одновременно по общему тактовому сигналу синхронизации С, который является счетным импульсом для всего счетчика. Схема синхронного счетчика на базе асинхронных T-триггеров приведена на рис рис. 9.19, б. Принцип ее работы аналогичен принципу работы первой схемы. Отличие заключается лишь в том, что вентили И во второй схеме объединяют не только единичные состояния выходов триггеров младших разрядов, но и пропускают эти единичные сигналы на входы триггеров последующих разрядов только при наличии тактового сигнала синхронизации C, т.е. одновременно. Задержка в обоих схемах равна времени срабатывания одного триггера.

Рис. 9.19. Схема синхронного четырехразрядного суммирующего счетчика с параллельным переносом на основе T-триггеров синхронных (а) и асинхронных (б).

Путем анализа работы обеих схем счетчиков рис. 9.19 несложно показать, что они являются суммирующими. Чтобы синтезировать схему вычитающего счетчика, необходимо использовать выходы триггеров с противополжными состояниями. Используя принцип коммутации прямых или инверсных выходов триггеров, можно реализовать реверсивный синхронный счетчик, изображенный на рис 9.20. Такой счетчик имеет два независимых тактовых входа для режимов суммирования C + и вычитания C -, которые также являются и стробирующими импульсами для вентилей И, коммутирующих прямые или инверсные выходы триггеров предыдущих разрядов на входы триггеров последующих разрядов. Такой счетчик называется еще двухканальным.

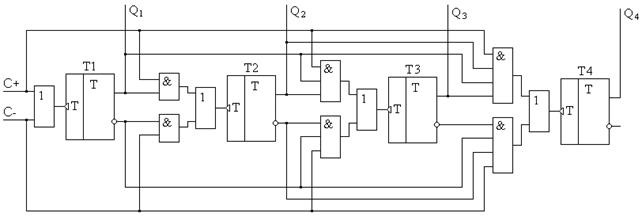
Рис. 9.20. Схема двухканального синхронного четырехразрядного реверсивного счетчика с параллельным переносом

Изображенные на рис.9.19 и рис.9.20 счетчики называются счетчиками с параллельным переносом, поскольку сигналы на все элементы И, формирующие единичные переносы, подаются с выходов триггеров одновременно в параллельном виде. Недостатком счетчиков с параллельным переносом является необходимость использования в случае увеличения разрядности счетчика элементов И с большим числом входов. При этом выходы триггеров должны обладать высокой нагрузочной способностью. Поэтому многоразрядные счетчики строят по групповому принципу. Согласно этому принципу, весь счетчик структурно реализуется путем соединения отдельных групп небольшой разрядности с параллельным переносом внутри этих групп. Сигнал переноса из очередной группы формируется элементом И, объединяющим выходы всех триггеров данной группы. Сформированный сигнал переноса предыдущей группы подается на счетный вход последующей группы. Общая задержка такого счетчика определяется суммой задержек каждой группы.

Другой вариант построения синхронного счетчика – это структура со сквозным переносом. В таких структурах перенос формируется с выходов триггеров только соседних разрядов, имеющих единичные уровни. Для этих целей достаточно использовать только двухвходовые элементы И при любой разрядности счетчика (рис. 9.21). Перенос между разрядами осуществляется через каждый элемент И (ЛЭ1 и ЛЭ2) в их последовательной структуре. Отсюда следует, что общее время срабатывания всего счетчика определяется временем срабатывания одного триггера и суммарным временем задержки последовательной цепи логических элементов И. Выигрыш по быстродействию в такой структуре осуществляется за счет меньшего времени срабатывания одного логического элемента по сравнению со временем срабатывания одного триггера. При достаточно большой разрядности счетчика, суммарное время задержки во всех элементах И может оказаться значительным и сравняться с временем срабатывания одного триггера, что недопустимо.

Рис. 9.21. Схема четырехразрядного суммирующего счетчика со сквозным переносом.

Дата добавления: 2015-05-09