І. Перевірка домашнього завдання

Хід уроку

Для груп Р-11, Д-11, С-11, М-11, В-11, Е-11

План-конспект уроку

Тема уроку: Тригонометричні функції числового аргументу. Періодичність тригонометричних функцій.

Мета уроку: Формування поняття тригонометричних функцій чис­лового аргументу; вивчення значень тригонометрич­них функцій деяких чисел (кутів), зміни знаків три­гонометричних функцій у координатних чвертях. Введення поняття періодичної функції; знаходжен­ня найменших додатних періодів тригонометричних функцій; формування умінь знаходити періоди функцій у = sin (kx + b), у = cos (kx + b), у = tg (kx + b), у = ctg (kx + b).

Розв'язування вправ аналогічних до домашніх.

1. Подайте в радіанній мірі кути:

а) 5°; б) 1140º; в) -765°; г) 67° 5'.

Відповідь: а) ; б) π; в) π; г) .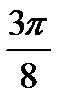

2. Подайте в градусній мірі кути:

а) 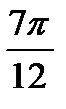, б) 1,25π; в) 1; г) 10.

Відповідь: а) 105°; б) 225°; в) 57,32°; г) 573,25°.

II. Сприймання і усвідомлення понять синуса, косинуса, тангенса і котангенса числа.

Розглянемо на координатній площині коло радіуса 1 з центром у початку коорди­нат, яке називається одиничним (рис. 43). Позначимо точку Р_о — правий кінець горизонтального діаметра. Поставимо у від­повідність кожному дійсному числу α точку кола за такими правилом:

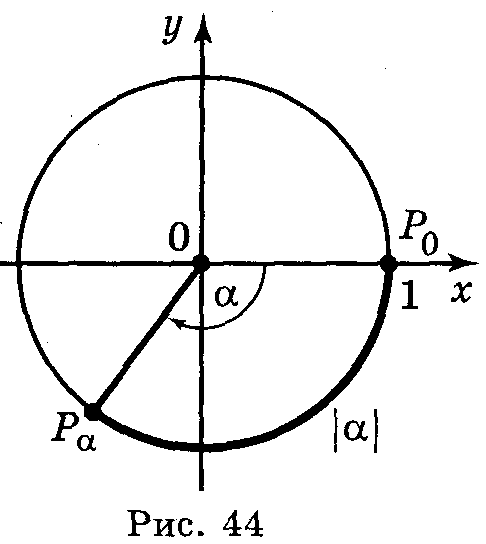1) Якщо α > 0, то, рухаючись по колу із точки Р_о в напрямі проти годинникової стрілки (додатний напрям обходу ко­ла), опишемо по колу шлях довжи­ною а, кінцева точка цього шляху і буде шуканою точкою Ρ_α.

2) Якщо α < 0, то, рухаючись із точки Ρ_о(рис. 44) в напрямі за годинниковою стрілкою, опишемо по колу шлях дов­жиною |α|; кінець цього шляху і буде шукана точка Р_α.

3) Якщо α = 0, то поставимо у відповідність точку Р_о.

Таким чином, кожному дійсному числу можна поставити у відповідність точку Ρ₀ одиничного кола.

Якщо α = α_о + 2 π k, де k — ціле число, то при повороті на кут α одержуємо одну і ту саму точку, що й при повороті на кут α_о.

Якщо точка Ρ відповідає числу α, то вона відповідає і всім числам виду α + 2 π k, де 2π — довжина кола (бо радіус дорівнює 1), а k — ціле число, що показує кількість повних обходів кола в ту чи іншу сторону.

!

Синусом числа α називається ордината точки Р_α, утвореної пово­ротом точки Р_α (1; 0) навколо початку координат на кут в α раді­ан (позначається sin α) (рис. 49). Синус визначений для будь-якого числа α.

!

Косинусом числа α називається абсциса точки Р_α, утвореної по­воротом точки Р_α (1; 0) навколо початку координат на кут в α радіан (позначається cos α) (рис. 49). Косинус визначений для будь-якого числа α.

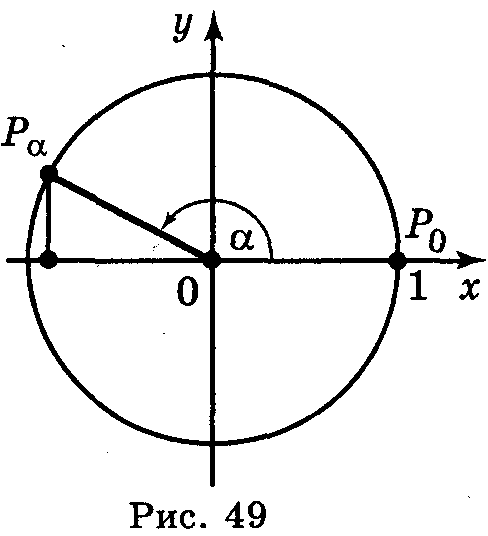Виконання вправ

1. Обчисліть:

a) cos 7π; б) sin 7π; в) cos 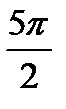; r) sin .

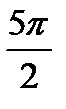Відповідь: а) -1; б) 0; в) 0; г) 1.

2. Обчисліть:

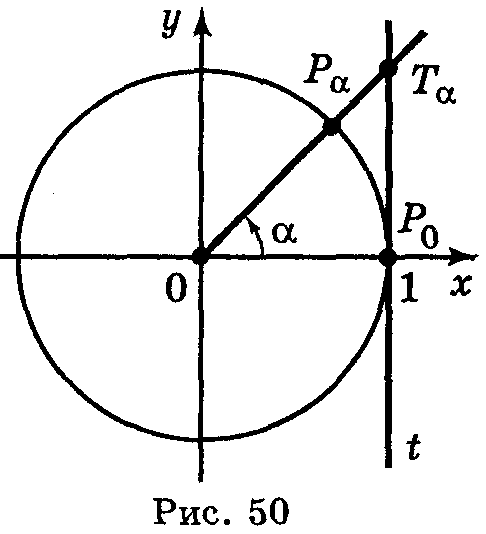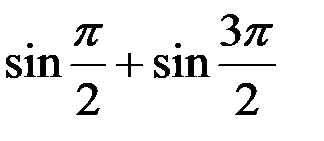a) ; б) ;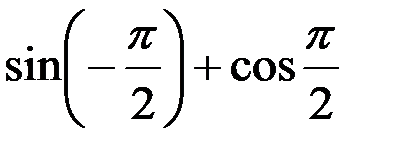

в) sin π + sin 1,5π; г) cos0 + cos 3,5π - cos 3π.

Відповідь: а) 0; б) -1; в) -1; г) 2.

!

Тангенсом числа α називається відношення синуса числа α до його косинуса: .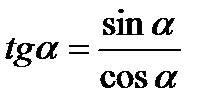

Тангенс визначений для всіх α, крім тих значень, для яких cos α = 0, тобто, α = + π n, n Ζ.

Для розв'язування деяких задач корисно мати уявлення про лінію тангенсів (рис. 50). Проведемо дотичну t до одиничного кола в точці Ρ_о. Нехай α — довільне число, для якого cos α 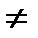0, тоді точка Р _α (cos α; sin α) не лежить на осі ординат і пряма ОР_α перетинає t в деякій точці Т _αз абсцисою 1. Знайдемо ординату точки Т_α із трикут­ника ОР_оТ _α.

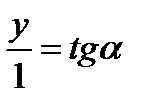; у = tgα.

Таким чином, ордината точки перетину прямих ОР _αі t дорівнює тангенсу числа α. Тому пряму t нази­вають віссю тангенсів.

!

Котангенсом числа α називається від­ношення косинуса числа α до його синуса: .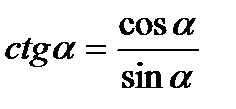

Котангенс визначений для всіх α, крім таких значень, для яких sin α 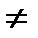0, тобто, α = π n, n Ζ.

Введемо поняття лінії котангенсів (рис. 51). Проведемо дотичну q до одиничного кола в точці . Для довільного числа α, якщо sin α 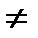0 і відповідно точка Р_α (cos α, sin α) не лежить на осі ОХ і тому пряма ОР _α перетинає пряму q у деякій точці Q_α з ординатою, що дорівнює 1. Із трикутника О Q_α маємо: 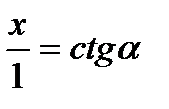, звідси х = ctg α. Таким чином, абсциса точки перетину прямої ОР _α і q дорівнює котангенсу числа α, тому пряму q називають віссю котангенсів.

Дата добавления: 2015-05-10