Теоретические сведения. Система линейных алгебраических уравнений имеет вид

Система линейных алгебраических уравнений имеет вид

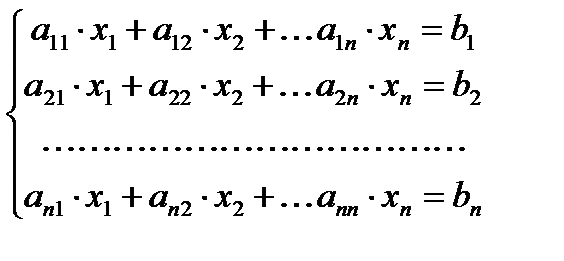(1)

или в матричной форм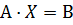е , где 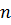– порядок системы, 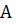- матрица коэффициентов, В - столбец свободных членов и X – столбец неизвестных.

, , .

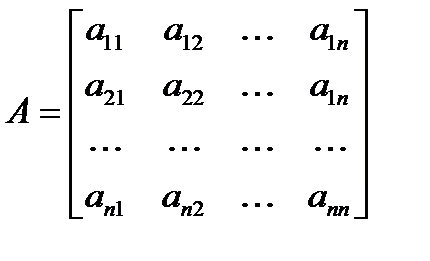Произвольная система уравнений вида (1) в общем случае может иметь единственное решение, не иметь решения или иметь бесконечное множество решений.

Методы численного решения системы линейных уравнений подразделяются на точные (конечные) и итерационные (бесконечные). Точные методы дают решение с помощью конечного числа арифметических операций, которые можно определить заранее. Итерационные методы дают решение системы уравнений как предел бесконечной последовательности приближений. На практике итерационный процесс прекращается при достижении заданной точности решения.

Метод исключения (метод Гаусса)

Метод Гаусса относится к точным. Решение системы из n уравнений выполняется в два этапа.

На первом этапе (прямой ход) исходная система уравнений (1) приводится к эквивалентной системе уравнений с треугольной матрицей коэффициентов. Прямой ход состоит из (n-1) шагов. На k-том шаге соответствующее уравнение вычитается из оставшихся уравнений с целью исключить k-тое неизвестное.

Введем (n-1) множителей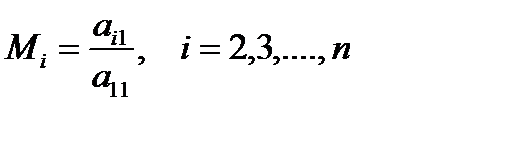

Вычтем из каждого i-го уравнения первое, домноженное на М_i. Предполагается, что а₁₁ не равно нулю. Введем обозначение

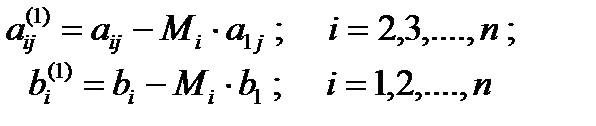
Для всех уравнений, начиная со второго, будут выполняться равенства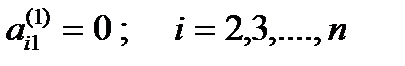

Преобразованная система уравнений запишется в следующем виде:

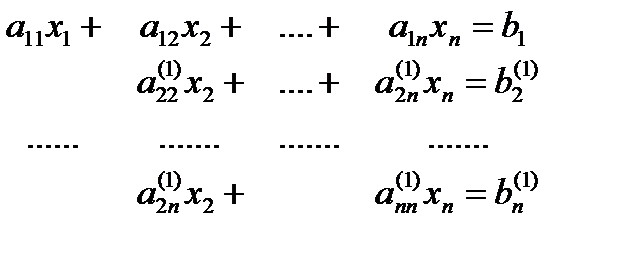
Таким же образом можно исключить x₂ из оставшихся (n-2) уравнений, затем x₃ из оставшихся (n-3) уравнений и т.д. На k-том этапе исключаем x_к с помощью множителей

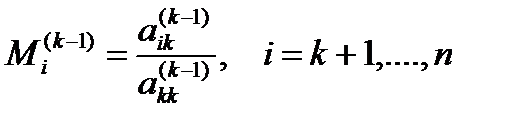
Предполагается, что коэффициенты 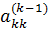не равны нулю. Новые значения коэффициентов системы уравнений и правых частей вычисляются по зависимостям

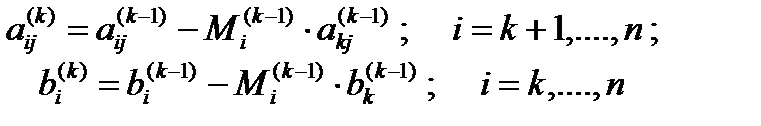
Индекс k принимает последовательные целые значения от 1 до (n-1) включительно и означает номер того уравнения, которое вычитается из остальных, а также номер того неизвестного, которое исключается из оставшихся (n-k) уравнений. При 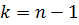из последнего уравнения исключается 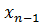неизвестное.

В результате выполнения прямого хода получается эквивалентная система линейных уравнений с треугольной матрицей коэффициентов вида

Точность решения системы линейных уравнений методом Гаусса в значительной степени зависит от значений коэффициентов М_i при исключении неизвестных. При минимальных абсолютных значениях М_i точность решений будет максимальной. Минимальные значения М_i имеют место при максимальных абсолютных значениях .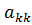

Выбор максимального коэффициента 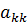осуществляется перестановкой уравнений. При этом необходимо добиться того, чтобы .

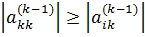Пример:

Приведём систему уравнений 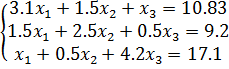к эквивалентной системе уравнений с треугольной матрицей коэффициентов:

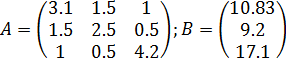
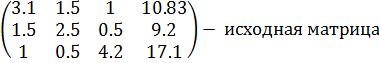
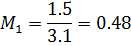
Домножим первую строку на 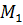и вычтем её из второй. При этом получим матрицу:

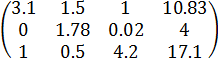
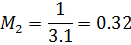
Домножим первую строку на 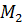и вычтем её из третей. При этом получим матрицу:

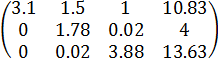
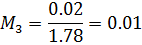
Домножим первую строку на 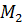и вычтем её из третей. При этом получим матрицу:

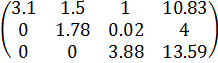
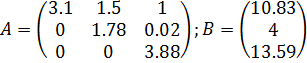
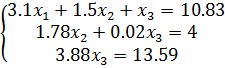
На втором этапе (обратном ходе) решения системы линейных уравнений находятся значения неизвестных по формулам

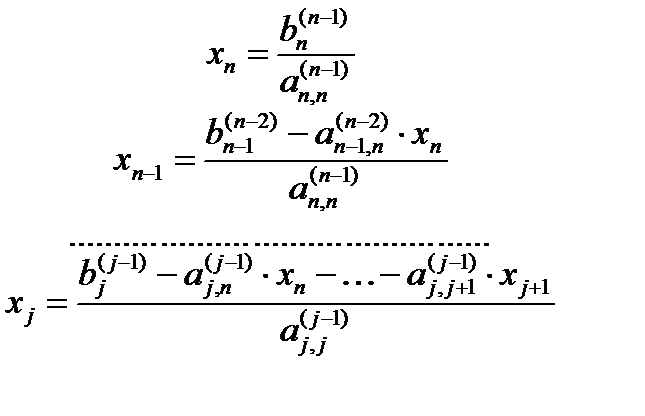
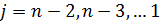
Общее число арифметических операций S, необходимых для решения системы уравнений (7.1) методом Гаусса определяется по формуле

, или для больших n

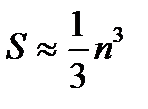
Пример:

Найдём значения неизвестных из полученной системы:

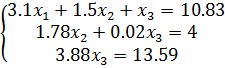
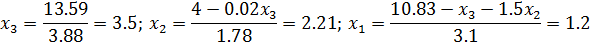
Дата добавления: 2015-05-10