Метод хорд и касательных

Метод касательных

Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где 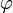— сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения 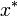должно выполняться условие 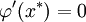. Решение данного уравнения ищут в виде 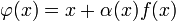, тогда:

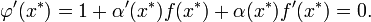
В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:

С учётом этого функция определяется выражением:

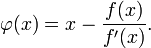
Эта функция в окрестности корня осуществляет сжимающее отображение^[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:

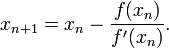
По теореме Банаха последовательность приближений стремится к корню уравнения .

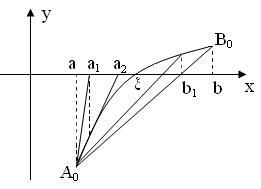
Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, тогда уточнение корня происходит быстрее.

Пусть дано уравнение f(x) = 0, корень отделен на отрезке [a, b].

Рассмотрим случай, когда f ‘(x) f ’’(x)>0:

В этом случае метод хорд дает приближенное значение корня с недостатком (конец b неподвижен), а метод касательных – с избытком (за начальное приближение берем точку b).

Тогда вычисления следует проводить по формулам:

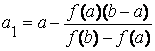
Теперь корень ξ заключен в интервале [a₁, b₁]. Применяя к этому отрезку комбинированный метод, получим:

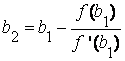
и т.д.

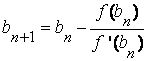
Если же f ‘(x) f ’’(x)<0, то, рассуждая аналогично, получим следующие формулы для уточнения корня уравнения:

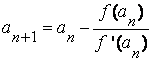
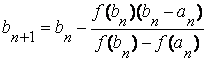
Вычислительный процесс прекращается, как только выполнится условие:

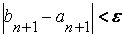
Дата добавления: 2015-05-10