Дисперсия параметра оптимизации

Проведение эксперимента

Дробный факторный эксперимент

Полный факторный эксперимент

Эксперимент, состоящий из всех возможных обработок, образованных двумя или более факторами, каждый из которых изучают на двух или более уровнях.

Эксперимент, состоящий из подмножества полного факторного эксперимента.

Каждый эксперимент содержит элемент неопределен­ности вследствие ограниченности экспериментального ма­териала. Постановка повторных (или параллельных) опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроиз­водимости). Эту ошибку и нужно оценить по параллель­ным опытам. Для этого опыт воспроизводится по возмож­ности в одинаковых условиях несколько раз и затем бе­рется среднее арифметическое всех результатов.

Все ошибки принято разделять на два класса: система­тические и случайные.

Систематические ошибки порождаются причинами, действующими регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и определить количественно.

Случайными ошибками называются те, которые появ­ляются нерегулярно, причины возникновения которых неизвестны и которые невозможно учесть заранее.

Дисперсия всего эксперимента получается в результате усреднения дисперсий всех опытов. По терми­нологии, принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра оптимизации 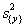или, что то же самое, дисперсии воспроизводимости эксперимента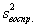

При подсчете дисперсии параметра оптимизации квад­рат разности между значением y_q в каждом опыте и средним значением из n повторных наблюдений y нужно просумми­ровать по числу опытов в матрице N, а затем разделить на N (n - 1):

,

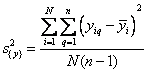Где i = 1, 2, …, N; q= 1, 2, …, n.

Такой формулой можно пользоваться в случаях, когда число повторных опытов одинаково во всей матрице.

Дисперсию воспроизводимости проще всего рассчиты­вать, когда соблюдается равенство числа повторных опы­тов во всех экспериментальных точках. На практике весь­ма часто приходится сталкиваться со случаями, когда число повторных опытов различно. Это происходит вследствие отброса грубых наблюдений, неуверенности экспе­риментатора в правильности некоторых результатов (в таких случаях возникает желание еще и еще раз повторить опыт) и т.п.

Тогда при усреднении дисперсий приходится пользо­ваться средним взвешенным значением дисперсий, взятым с учетом числа степеней свободы

,

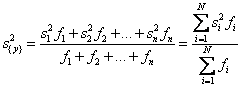где

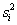– дисперсия i -го опыта;

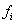– число степеней свободы i -м опыте, равное числу параллельных опытов n_i минус 1.

Число степеней свободы средней дисперсии принима­ется равным сумме чисел степеней свободы дисперсий, из которых она вычислена.

Случай с неравным числом наблюдений, который мы рассмотрели выше, связан с нарушением ортогональности матрицы. Поэтому здесь нельзя использовать расчетные формулы для коэффициентов, приведенные ранее. Этот вопрос будет рассмотрен ниже.

Экспериментатору не следует забывать о про­верке однородности дисперсий, неоднородные дисперсии усреднять нельзя. Прежде чем пользоваться приведёнными выше формулами, нужно убедиться в однородности суммируемых дисперсий.

Дата добавления: 2015-05-10