Проверка значимости коэффициентов

Проверка адекватности модели

Регрессионный анализ

Регрессионный анализ как всякий статистический метод, применим при определенных предположениях, постулатах.

Первый постулат. Параметр оптимизации y есть случайная величина с нормальным законом распределения. Дисперсия воспроизводимости – одна из харак­теристик этого закона распределения.

Второй постулат. Дисперсия y не зависит от абсо­лютной величины y.

Третий постулат. Значения факторов суть неслу­чайные величины

Проверить адекватность модели – значит установить, насколько хорошо модель описывает реальные процессы, происходящие в системе, насколько качественно она будет прогнозировать развитие данных процессов. Проверка адекватности проводится на основании некоторой экспериментальной информации, полученной на этапе функционирования системы или при проведении специального эксперимента, в ходе которого наблюдаются интересующие процессы.

Проверка значимости каждого коэффициента прово­дится независимо.

Ее можно осуществлять двумя равноценными спосо­бами: проверкой по t -критерию Стьюдента или построе­нием доверительного интервала. При использовании пол­ного факторного эксперимента или регулярных дробных реплик доверительные интервалы для всех коэффициен­тов (в том числе и эффектов взаимодействия) равны друг другу. Прежде всего, надо найти дисперсию коэф­фициента регрессии 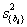. Она определяется в нашем по формуле

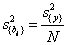
Из формулы видно, что дисперсии всех коэффициентов равны друг другу, так как они зависят только от ошибки опыта и числа опытов.

Теперь легко построить доверительный интервал

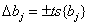
Здесь t – табличное значение критерия Стьюдента при числе степеней свободы, с которыми определялась 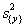, и выбранном уровне значимости (обычно 0,05); 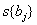– квадратичная ошибка коэффициента регрессии.

Коэффициент значим, если его абсолютная величина больше доверительного интервала.

Дата добавления: 2015-05-10