Краткая теория

РАБОТА 1

И РАСЧЕТА ИХ ПОГРЕШНОСТЕЙ.

ОСВОЕНИЕ МЕТОДОВ ПРОВЕДЕНИЯ ИЗМЕРЕНИЙ

ЦЕЛЬ РАБОТЫ: рассмотреть простейшие методы измерений линейных величин и получить навыки обработки прямых и косвенных измерений; ознакомиться с методом наименьших квадратов.

ОБОРУДОВАНИЕ: штангенциркуль, микрометр, образцы для измерений, установка для определения удельного сопротивления проволоки.

Для определения длины и расстояний применяются самые разнообразные способы, выбор которых определяется необходимой степенью точности и условий эксперимента. Для непосредственного измерения длины широко применяется масштабная линейка с сантиметровыми и миллиметровыми делениями.

Ценой деления шкалы любого прибора называется разность значений величины, соответствующих 2 соседним отметкам шкалы. Для масштабной линейки она составляет 1 мм. При измерении максимальная ошибка не превосходит половины цены деления шкалы, поэтому точность измерения масштабной линейки не превышает, таким образом, половины цены деления, т.е. 0,5 мм.

Если необходимо произвести измерения с большей точностью, пользуются приборами, снабженными нониусами (см. ниже), например, штангенциркулем. Точность приборов в этом случае 0,1-0,01 основного деления. Для измерения малых размеров (толщины, радиуса проволоки и т.д.) применяются приборы, снабженные микрометрическим винтом. Так очень распространен микрометр, которым можно измерять с точностью 0,01-0,005 мм.

Познакомьтесь с некоторыми из методов измерений.

МЕТОД ЛИНЕЙНОГО НОНИУСА.

Нониусом называется небольшая дополнительная шкала к обычному масштабу, позволяющая увеличивать точность в 10-20 раз. Линейным нониусом называется маленькая линейка с делениями, которая может скользить вдоль большой линейки также с делениями, называемой масштабом.

Деления на нониусе наносятся обычно так, что одно деление нониуса составляет 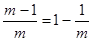делений масштаба, где m – число делений нониуса.

Именно это позволяет, пользуясь нониусом, производить отсчеты с точностью до1/m части наименьшего деления масштаба. Пусть расстояние между соседними штрихами масштаба y, а между соседними штрихами нониуса x. Можно записать, что x = y - (y/m).Величина Dx = y - x = y/mносит название точности нониуса. В любом положении нониуса относительно масштаба одно из делений первого совпадает с каким-либо делением второго. Отсчет по нониусу основан именно на способности глаза фиксировать это совпадение делений нониуса и масштаба.

Рассмотрим теперь процесс измерения при помощи линейного нониуса. Пусть L — измеряемый отрезок

Совместим с его началом нулевое деление основного масштаба. Пусть при этом конец его окажется между k и (k+1) делением этого масштаба. Тогда можно записать L = ky + DL, где DL — неизвестная пока доля k-го деления масштаба.

Приложим теперь к концу отрезка L наш нониус так, чтобы нуль нониуса совпадал с концом этого отрезка. Так как деления нониуса не равны делениям масштаба, то обязательно найдется на нем такое деление n, которое будет ближе всего подходить к соответствующему (k+n) делению масштаба. Как видно из рис.1,

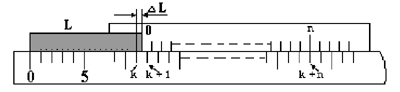
Рис.1 Схема нониуса

DL = ny - nx = n(y - x) = n Dx,

и вся длина будет равна L = ky + nDx или L = ky + n (y/m),

что можно сформулировать так: длина отрезка, измеряемого при помощи нониуса, равна числу целых делений масштаба плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторыми делениями масштаба. Погрешность нониуса принимают равной его точности.

Штангенциркуль (рис.2) состоит из разделенного на миллиметры масштаба М, вдоль которого может перемещаться ножка FB с зажимным винтом С. В обойме сделан вырез против делений масштаба, на скошенном краю которого, прилегающем к масштабу, нанесен нониус. Цена деления обычно 0,1; 0,05; 0,02 мм.

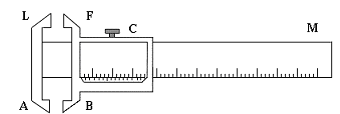
Рис.2. Схема штангенциркуля.

При нулевом показании нуль нониуса совпадает с нулем масштаба. Неподвижная ножка LA служит упором для измеряемого тела, части обеих ножек АВ - для измерения внутренних размеров тела.

Дата добавления: 2015-05-10