Меры вариаций рядов распределений

Меры вариации – это показатели, которые учитывают количество отклонений от мер центральной тенденции (Меры центральной тенденции – это показатели, которые характеризуют всю изучаемую совокупность респондентов одним числом.Например, средний возраст, модальная национальность, медианный доход.). Меры вариации — показатели колеблемости значений некоторого признака у индивидов данной совокупности. Одна из простейших мер — вариационный размах, равный разности крайних (наибольшего и наименьшего) значений признака в данной совокупности.

Важнейшим показателем колеблемости является дисперсия. Т. к. из-за компенсации отклонений индивидуальных значений от М (Меры центральной тенденции), имеющих разные знаки, сумма всех отклонений равна нулю, в качестве М. в. используется сумма квадратов отклонений, приходящаяся на одно наблюдение. Эта величина и называется дисперсией (D).

Дисперсия – это среднеарифметическое квадратов отклонений вариантов от среднего арифметического значения признака для данной совокупности, т.е.

- Среднее арифметическое отклонение

*100% - процент отклонения от среднего арифметического

(- коэффициент вариации)

Различают:

- общую дисперсию - измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.

- внутригрупповая дисперсию - Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

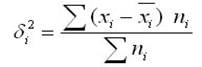
где хi — групповая средняя;

ni — число единиц в группе.

- среднюю из внутригрупповых дисперсий - средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

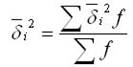
- межгрупповая дисперсию - характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.

Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.

Свойства дисперсии:

1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.

2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.

Особаяценность Д., вычисленной по выборке, состоит в том, чтоонаявляетсянесмещеннойоценкой Д. генеральнойсовокупности - ср.: выборочноестандартноеотклонениеявляетсясостоятельной, носмещеннойоценкой стандартного отклонениягенеральнойсовокупности.

Дата добавления: 2015-05-10