Численная модель траектории полета ЛА

Полученную систему дифференциальных уравнений первого порядка c заданными начальными условиями можно решить различными способами.

Одним из наиболее распространенных методов решения обыкновенных дифференциальных уравнений является метод конечных разностей (МКР). Рассмотрим применение МКР для численного решения на ЭВМ простейшего дифференциального уравнения первого порядка:

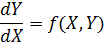
с начальными условиями X ₀, Y (X ₀) = Y ₀.

Решение будем искать в интервале [ X ₀ , b ] и будем полагать, что функция на данном интервале удовлетворяет условиям гладкости.

Разобьем область аргумента Х на множество отрезков длиной Δ X и разложим функцию Y в ряд Тейлора в окрестности произвольной точки X_i из области существования функции:

.
Отбрасывая члены ряда, содержащие производные второго и высшего порядков, получаем конечно-разностное выражение первой производной

.

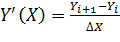Отсюда

Вычисляя последовательно от начального значения Y ₀ значения Y ₁, Y ₂, Y ₃,... по данной формуле, находим искомое решение.

На рис. 2 показана форма численного решения, получаемого с помощью таких вычислений

Рис.2. Схема приближенного решения методом Эйлера

Данный метод решения обыкновенного дифференциального уравнения носит название метода Эйлера. При достаточно малых величинах шага метод Эйлера дает решение с большой точностью, так как погрешность близка к 0() на каждом шаге процесса.

Для решения системы уравнений траектории методом Эйлера запишем в конечно-разностном виде проекции производной скорости:

,

тогда уравнения (4)-(5) примут следующий вид

,

,

где i – номер текущего шага по времени.

Выразим в этих уравнениях в явном виде

. (10)

Решая систему уравнений (10) на каждом шаге по времени, можно последовательно вычислить все точки траектории полета ЛА.

Дата добавления: 2015-05-10