
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производные высших порядков
|
|
|
|
4. 981-989
3. 937-944
2. 874-944
1. 849-864
Четыре темы
Описание установки
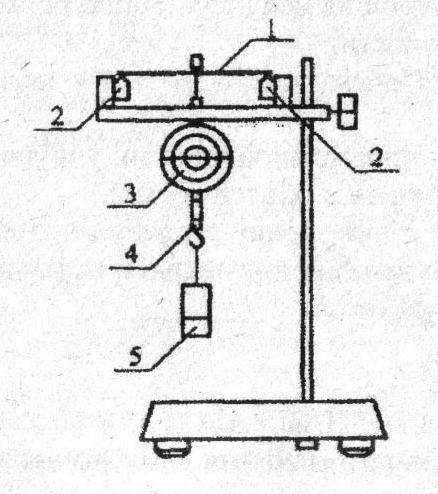
| Измерения | F,(H) | L1(F) | |||||||
| Материал | Модуль Юнга 10 H\M*M |
| Сталь | |
| Железо | |
| Латунь | |
| Медь | |
| Аллюминий | |
| Серебро | |
| Бронза |
| Титан |
Хайкин С.Э. Физические основы механики. – М.: Наука, 1971.
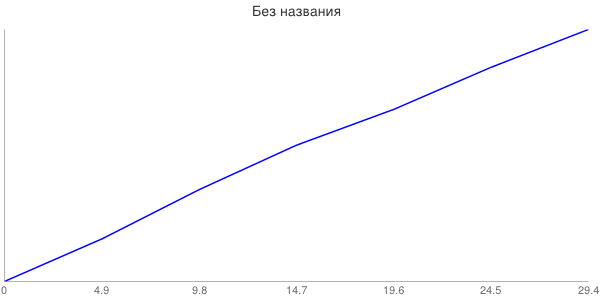
График
Сложная функция.
Пример. Найти производную функции  .
.
Сначала преобразуем данную функцию: 

Пример. Найти производную функции  .
.

Пример. Найти производную функции 

Пример. Найти производную функции 

Логарифмическое дифференцирование.
Пример. Найти производную функции  .
.
По полученной выше формуле получаем: 
Производные этих функций: 
Окончательно:

Производная неявно заданной функции
Пример. Найти производную функции у, заданную уравнением
х3+у3-3ху=0.
Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения  следует, что
следует, что  , т.е.
, т.е.  .
.
Производная функции, заданной параметрически
 .
.
Пример. Пусть  . Найти
. Найти  .
.
Имеем  , следовательно
, следовательно  , т.е.
, т.е.  .
.
Пусть функция f(x) – дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную
 .
.
Если найти производную функции f¢(x), получим вторую производную функции f(x).

т.е. y¢¢ = (y¢)¢ или  .
.
Этот процесс можно продолжить и далее, находя производные степени n.
 .
.
Пример. Найти производную второго порядка  для функции
для функции  .
.
Найдем сначала производную первого порядка данной функции:

Полученный результат продифференцируем еще раз:

ДОМАШНЕЕ ЗАДАНИЕ ИЗ МИНОРСКОГО
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 323; Нарушение авторских прав?; Мы поможем в написании вашей работы!