Надежность системы с нагруженным резервированием

Нагруженное резервирование, т.е. резервные элементы эксплуатируются в тех же режимах, что и основные. При нагруженном резервировании интенсивность отказов основных и резервных элементов одинакова, а увеличение ресурса осуществляется за счет облегченного режима эксплуатации.

Рассмотрим систему, состоящую из n элементов, один из которых основной n и n-1 резервные.

При условии что отказы элементов независимы данная система сохраняет работоспособность при работоспособности хотя бы одного из её элементов.

Поскольку отказ системы событие заключающееся в одновременном появлении группы случайных независимых событий (отказов элементов), то вероятность отказа системы определим как произведение вероятности отказов её элементов: Qc(t)=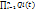

Соответственно вероятность безотказной работы будет определяться:

Pc(t)=1-Qc(t)= 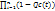=1- .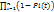

В период нормальной эксплуатации наработка до отказ описывается экспоненциальным распределением: Pi(t)=exp(-λt).

Pc(t)=1- .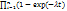

Если нам будет необходимо определить вероятность отказа системы то: Qc(t)=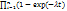

T₀=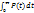

Выполнив интегрирование численным методом получим: Т₀=(1/λ_i)*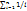

Основная система
Неидентичные элементы	идентичные элементы
P: Рс(t)= 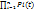Q: Qc(t)=1- 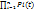T0: Т0=1/λ0.	Pi(t)=exp(-λt)^n Qc(t)=1-P^n(t) T0=n*1/λi
Система с резервированием
неидентичные	идентичные
Р: Pc(t)=1- 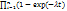Q: Qc(t)= 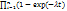T0: Т0=(1/λi)*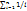	Pc(t)=1-(1-exp(-λt))^n Qc(t)=1-(1-exp(-λt))^n Tc=n*1/λ*1/i

Для систем с идентичными элементами на практике решаются следующие задачи оптимизации:

1 задача: определение числа элементов системы при котором вероятность её отказа не привышала бы заданной – Qⁿ(t)≤Q_c(t), n≤ ln(1/Qc)/ln(1/Qi)

2 задача: определение надежности каждого элемента исходя из требования надежности системы.

Дата добавления: 2015-05-10