Наглядное изображение

Обозначения графические материалов в сечениях

ГОСТ 2.306 – 68

Геометрические тела, отображаемые на чертеже, предполагается изготавливать из тех или иных материалов. Материал указывается в основной надписи чертежа, а если на чертеже нужно указать сечение, предусмотрено графическое обозначение материалов в зависимости от вида. Обозначения материалов в сечениях приведены ниже.

• Металлы и твердые сплавы
• Неметаллические материалы
• Древесина
• Камень естественный
• Керамика и силикатные материалы для кладки
• Бетон
• Стекло и другие светопрозрачные материалы
• Жидкости
• Грунт естественный

Допускается применять дополнительные обозначения материалов, не предусмотренных стандартом, поясняя их на чертеже.

Построение наглядных изображений

Проецирование

Построение наглядных изображений начинается с проведения осей. Положение осей. Оси кабинетной проекции располагают, а: ось х — горизонтально, ось г — вертикально, ось у — под углом 45° к горизонтальной линии. Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°. Ось у проводят с наклоном влево или вправо. В кабинетной проекции по осям х и у (и параллельно им) откладывают натуральные размеры. По оси у (и параллельно ей) размеры сокращают в два раза. Положение осей изометрической проекции. Оси х и у располагают под углом 30° к горизонтальной линии (120° между осями). Их удобно также проводить при помощи угольника. Но в отличие от предыдущего случая угольник берут с углами 30, 60 и 90°. При построении изометрии по осям х, у, z и параллельно им откладывают натуральные размеры предмета. Показано построение осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали квадратных клеток. Отношение отрезков в 3 и 5 клеток дает наклон оси в 30°. Наглядные изображения предметов. Рассмотрим общий способ построения наглядных изображений на примере детали, три вида которой даны. Из рассмотренного в таблице примера видно, что правила построения кабинетной и изометрической проекций в общем одинаковы. Разница заключается в расположении осей и в длине отрезков, откладываемых вдоль оси у. Наглядные изображения плоских фигур. Вы рассмотрели общий способ построения наглядных изображений. Однако бывают случаи, когда этот способ легче применить, начиная построение с фигуры основания. Поэтому рассмотрим способ построения наглядных изображений плоских геометрических фигур, расположенных горизонтально.

1. Понятие об аксонометрических проекциях и их применение. Аксонометрическими (Аксонометрия в переводе с греческого языка («ахоп» — ось; «metreo» — измеряю) означает осемерное изображение.) проекциями называют изображения, полученные путем проектирования параллельными лучами фигуры (предмета) вместе с осями координат на произвольно расположенную плоскость, которую называют «аксонометрической» (или картинной). Обычно плоскость (или предмет) располагают так, чтобы на аксонометрической проекции предмета были видны три стороны: верхняя (или нижняя), передняя и левая (или правая).
Основным достоинством аксонометрических проекций является наглядность и представление о величине изображенного предмета, поэтому их применяют в качестве иллюстрации к чертежу для облегчения понимания конструктивной формы предмета. На (фиг.270) показано получение аксонометрической проекции детали.

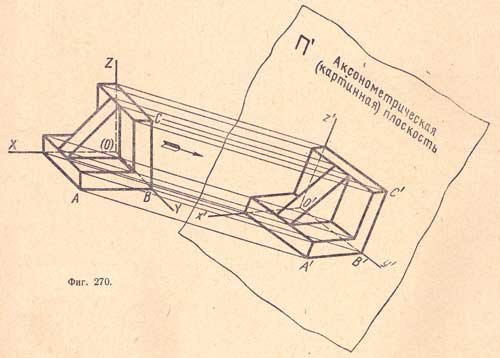
На аксонометрических проекциях приняты следующие обозначения: аксонометрическая плоскость обозначается П'; аксонометрические оси координат - х', у', z'; аксонометрические проекции точек A, В и т.д. обозначаются А', В' и т.д. Начало координат обозначается О'.
2. Виды аксонометрических проекций.
В зависимости от направления проектирующих лучей аксонометрические проекции разделяются на: прямоугольные или ортогональные (проектирующие лучи перпендикулярны аксонометрической плоскости П') и косоугольные (проектирующие лучи наклонены к аксонометрической плоскости).
В зависимости от наклона осей координат к аксонометрической плоскости, а следовательно, от степени уменьшения размеров аксонометрических проекций отрезков, имеющих направление осей координат (Известно, что отрезок прямой, наклоненный к плоскости, проектируется на нее уменьшенным; чем больше будет угол наклона, тем меньших размеров будет проекция отрезка.), - все аксонометрические проекции делятся на три основных вида:
1) изометрические, т.е. одинакового измерения (оси z', х' и у' наклонены одинаково; следовательно, уменьшение размеров по направлению всех трех осей одинаковое);
2) диметрические, т. е. двойного измерения (две оси координат имеют один и тот же наклон, а третья - другой; следовательно, уменьшение размеров по этим двум осям будет одно и то же, а по третьей оси - другое);
3) триметрические, т.е. тройного измерения (все оси имеют разный наклон; следовательно, уменьшение размеров по направлению всех трех осей разное).
В машиностроительном черчении из прямоугольных аксонометрических проекций чаще всего применяют изометрическую и диметриче-скую, а из косоугольных - диметрическую, которую иначе называют фронтальной диметрической проекцией.
3. Изображение аксонометрических осей и показатели искажения. В изометрической проекции углы между аксонометрическими осями х', у' и z' одинаковы (по 120°); ось z' расположена вертикально; следовательно, оси х' и у' наклонены к горизонтальной линии на угол 30° (фиг.271,а).

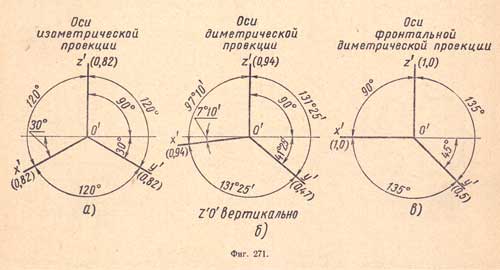
При таком положении осей показатели искажения для всех осей одинаковы и равны 0,82.
Показателем искажения называют отношение размера аксонометрической проекции отрезка, имеющего направление какой-либо оси координат, к его действительному размеру. Например, при действительном размере 100 мм и показателе искажения 0,82 размер аксонометрической проекции равен 100 × 0,82 = 82 мм.
В диметрической проекции угол между аксонометрическими осями z' и х' равен 97°10', а углы между аксонометрическими осями х' и у', а также z' и у' одинаковы, т.е. по 131°25'. Аксонометрическая ось z' имеет вертикальное положение, следовательно, ось х' наклонена к горизонтальной линии на угол 7°10' а ось у' на угол 41° 25' (фиг.271,б).
При таком наклоне аксонометрических осей показатель искажения для осей z' и х' равен 0,94, а для оси у' - 0,47.
Во фронтальной диметрической проекции угол между аксонометрическими осями z' и х' равен 90°, а углы между аксонометрическими осями х' и у', а также между аксонометрическими осями z' и y' одинаковы, т. е. по 135°. Ось z' имеет вертикальное положение, следовательно, ось х' будет иметь горизонтальное положение, а ось у' наклонена к горизонтальной линии на угол 45° (фиг.271,в).
Показатели искажения по аксонометрическим осям х' и z' равны 1,0 а по оси у' - 0,5.
Такую фронтальную диметрическую проекцию называют кабинетной; ее рекомендуется применять тогда, когда хотят показать без изменения очертания фигур, расположенных в плоскостях, параллельных фронтальной плоскости проекций.
Для сравнения изображений, выполненных в аксонометрических проекциях, на (фиг.272) показаны различные аксонометрические проекции одного и того же куба.

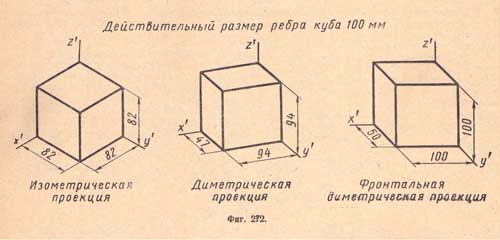
Для упрощения вычисления показателей искажения ГОСТ 3453-59 рекомендует строить изометрическую проекцию без сокращения по аксонометрическим осям x', у' и z', а диметрическую проекцию без сокращения по аксонометрическим осям х' и y', и с сокращением 0,5 по аксонометрической оси у'. В этом случае изображение получается несколько увеличенным, но наглядность его не ухудшается.

1. Построение аксонометрических осей координат. Аксонометрические оси х' и у' для изометрической и кабинетной проекций наклонены по отношению к горизонтальной линии на углы в 30 и 45° и не требуют объяснений для их построения.
Построение аксонометрической оси х для диметрической проекции, наклоненной на угол 7°10', и оси у', наклоненной на угол 41° 25', рекомендуется выполнять в такой последовательности:
а) намечают точку О' - начало координат; проводят аксонометрическую ось z (вертикально); приняв за центр точку О', проводят слева дугу произвольного радиуса R, получают точку А (фиг.273,а).

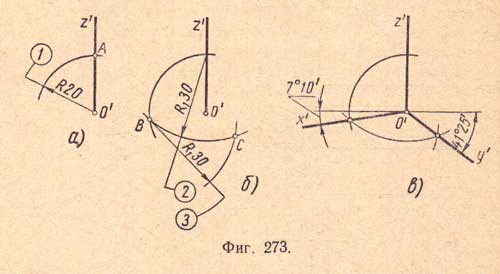
б) приняв за центр точку А, проводят дугу R₁ - 1,5R, получают точку В; приняв за центр точку В, проводят дугу тем же радиусом R₁ и получают точку С (фиг.273,б);
в) из точки О' проводят лучи через точки В и С (фиг.273,в). Эти лучи явятся аксонометрическими осями х' (7° 10') и у' (41° 25').
2. Построение аксонометрической проекции точки. Даны ортогональные проекции A₁, A₂, А₃ точки А (фиг.274,a) (координаты х =20, у = 30, z = 40).

ПОСТРОЕНИЕ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ ОКРУЖНОСТИ.

1. Построение изометрической проекции окружности, лежащей в одной из плоскостей проекции.
I, а. Дана окружность диаметра D, лежащая в плоскости П₁ (фиг.278). Намечаем на ней несколько равномерно расположенных (но не менее восьми) точек, проекции которых на плоскости П₁ обозначим А₁,В₁,С₁,D₁,Е₁,F₁,G₁,H₁. Определяем их координаты.

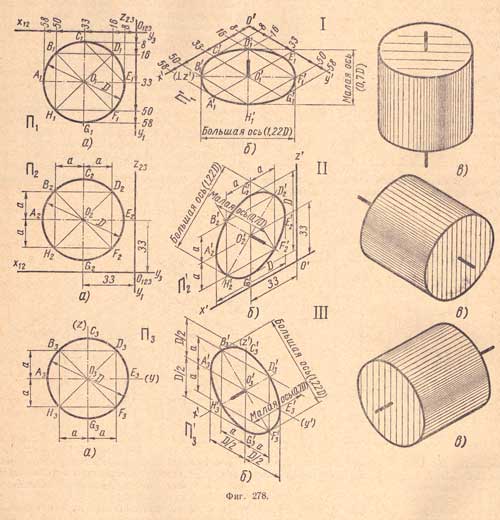
I, б. Проводим аксонометрические оси х' и у' и строим на плоскости Щ вторичные изометрические проекции всех указанных точек. Соединив их плавной замкнутой кривой, получим вторичную и вместе с тем изометрическую проекцию данной окружности - эллипс, у которого малая ось будет иметь направление не лежащей в данной плоскости изометрической оси г (т. е. вертикальной) и равняться 0,7 D, а большая ось будет перпендикулярна малой оси (т. е. иметь горизонтальное направление) и равняться 1,22 D.
I, в. Показан пример применения изометрической проекции круга, лежащего в горизонтальной плоскости, при изображении изометрической проекции цилиндра.
II, а. Дана ортогональная проекция той же окружности, но лежащей в плоскости П₂. Вместо того, чтобы определять координаты всех намеченных точек, можно определять только координаты центра О₂ и размеры а и а от центровых линий до намеченных точек В₂,D₂,H₂,F₂.
II, б. Построение вторичной и вместе с тем изометрической проекции этой окружности аналогично указанному на (фиг.278, I, б). Малая ось полученного эллипса расположена по направлению не лежащей в д'анной плоскости аксонометрической оси у', а большая ось перпендикулярна ей.
Длина осей эллипса такая же, как и на (фиг.278, I, б).
II, в. Показан пример применения изометрической проекции окружности, лежащей во фронтальной плоскости при изображении цилиндра.
III, а. Дана ортогональная проекция той же окружности, но лежащей в плоскости П₃; центр окружности не координирован. Определяем размеры а и а от центровых линий до намеченных точек В₃, D₃, F₃ и Н₃.
III, б. Построение эллипса начинаем с проведения прямых, заменяющих аксонометрические оси z и у, затем через полученную в пересечении точку O₃ проводим линию малой оси по направлению не лежащей в данной плоскости аксонометрической оси х и линию большой оси, перпендикулярную к малой оси; в остальном построение эллипса аналогично указанному на чертеже II, б. Малая ось эллипса расположена по направлению не лежащей в данной плоскости аксонометрической оси х', а большая перпендикулярна ей.
III, в. Показан пример применения изометрической проекции окружности, лежащей в профильной плоскости, при изображении цилиндра. Обычно при выполнении аксонометрических проекций заменяют эллипс очень близким ему по очертанию и размерам овалом, построение которого гораздо проще.

22. КОСОУГОЛЬНЫЕ ПРОЕКЦИИ

Дата добавления: 2015-05-26