Свойства операций над множествами

Задание множеств

Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:

а) перечислением элементов: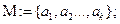

б) характеристическим предикатом:

в) порождающей процедурой:

Примеры:

а)

б)

в) {n | for n from 1 to 9 yield n }.

1.3 Операции над множествами

Самого по себе понятия множества еще недостаточно — нужно определить способы конструирования новых множеств из уже имеющихся, то есть операции над множествами.

Сравнение множеств. Множество А содержится в множестве В (множество В включает множество А), если каждый элемент А есть элемент В:

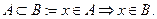
В этом случае А называется подмножеством В, В – надмножеством А.

Если и 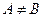, то А называется собственным подмножеством В. Заметим, что 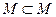. По определению .

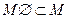Два множества равны, если они являются подмножествами друг друга:

.

Мощность множества М обозначается как |М |. Для конечных множеств мощность — это число элементов. Например, | | = 0, но |{ }| = 1. Если |A| = |В|, то множества А и В называются равномощными.

Обычно рассматриваются следующие операции над множествами:

а) объединение:

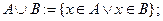
б) пересечение:

в) разность:

г) симметрическая разность:

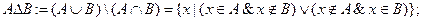
д) дополнение:

Операция дополнения подразумевает некоторый универсум .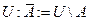

Пример.

Пусть А: ={1,2,3}, В:={3,4,5}.

Тогда: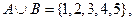

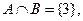
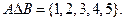
На рис 1.1 приведены диаграммы Венна, иллюстрирующие операции над множествами. Сами исходные множества изображаются фигурами (в данном случае овалами), а результат графически выделяется (в данном случае для выделения использована штриховка).

Рис. 1.1. Операции над множествами

Пусть задан универсум U. Тогда 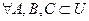выполняются следующие свойства:

1. идемпотентность:

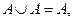
2. коммутативность:

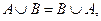
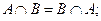
3. ассоциативность:

;

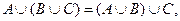
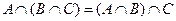4. дистрибутивность:

;

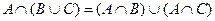5. поглощение:

;

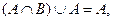
6. свойства нуля:

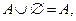
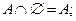
7. свойства единицы:

,

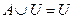8. инволютивность:

Пояснение: В справедливости перечисленных свойств можно убедиться различными способами. Например, нарисовать диаграммы Венна для левой и правой частей равенства и убедиться, что они совпадают, или же провести формальное рассуждение для каждого равенства. Рассмотрим для примера первое равенство: . Возьмем произвольный элемент x, принадлежащий левой части равенства, 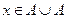. По определению операции объединения имеем . В любом случае . Взяв произвольный элемент из множества в левой части равенства, обнаружили, что он принадлежит множеству в правой части. Отсюда по определению включения множеств получаем, что 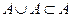. Пусть теперь . Тогда, очевидно, верно . Отсюда по определению операции объединения имеем 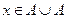. Таким образом, 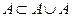. Следовательно, по определению равенства множеств, . Аналогичные рассуждения нетрудно провести и для остальных равенств.

Дата добавления: 2015-05-26