Розподіл Максвела-Больцмана

Нерівність Клаузіуса

ККД у всіх обернених теплових машин в яких використовується обернений цикл Карно і які працюють в ідентичних умовах – однаковий, а ККД необернених теплових машин завжди менше, ніж обернених. Тоді можна знайти деяке загальне для всіх машин відношення між кількістю теплоти циклів і температурами джерел теплоти.

Для обернених циклів на основі рівняння (3) отримуємо:

.

Для необернених циклів:

.

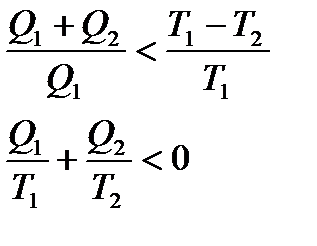Якщо об’єднати співвідношення між кількостями теплоти і температурами джерел теплоти для обернених і необернених процесів, отримаємо:

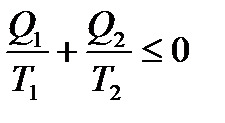. (7)

Це рівняння - нерівність Клаузіуса.

Закон розподілу Больцмана – закон розподілу молекул по потенціальним енергіям.

Закон розподілу Максвела – закон розподілу по кінетичним енергіям.

Якщо об’єднати ці два закони, отримаємо закон розподілу молекул по повним енергіям. Таке об’єднання можливе на основі теореми про вірогідність складної події. Згідно рівняння (1), кількість молекул, що попадає в межі об’єму dV:

.

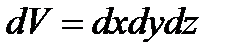Розташованого в точці (x;y;z) дорівнює:

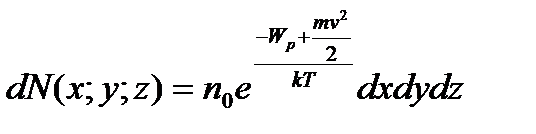, (14)

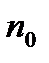- число молекул в одиниці об’єму.

З урахуванням закону Максвела, число молекул, компоненти швидкостей яких лежать у межах 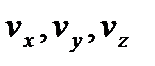до 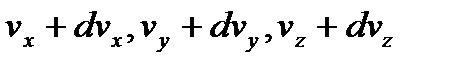, а координати в межах від x,y,z до x+dx, y+dy, z+dz будуть рівними, тоді напишемо:

,

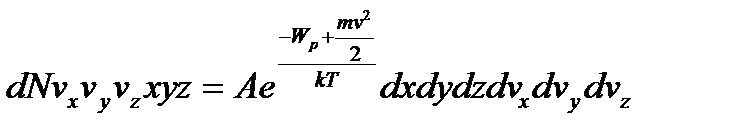А – нормуючий множник, .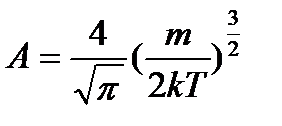

У рівнянні потенціальна і кінетична енергія, а відповідно і повна енергія можуть приймати неперервний ряд значень. Якщо повна енергія частинок може приймати лише дискретний ряд значень 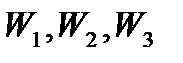, то розподіл Максвела-Больцмана має вигляд:

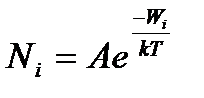, (15)

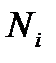- число частинок в стані з енергіями ;

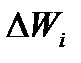А - коефіцієнт пропорційності, який має задовольняти умови ;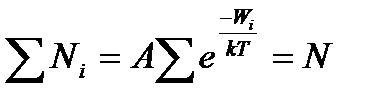

N - певне число частинок, що розглядаються в даній системі.

Якщо підставити значення в рівняння (15), то отриманий кінцевий вираз закону розподілу мікрочастинок по дискретним значенням енергії:

.

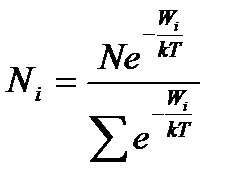4. Дефекти в кристалах

Дефектами кристалів називаються порушення ідеальної кристалічної структури. Таке порушення може полягати у відсутності атома у вузлі гратки (вакансія), в заміні атома даної речовини (свого атома) чужими атомами (атомом домішок), у внесенні зайвого атома (свого чи чужого) у міжвузольний простір. Подібні дефекти називаються точковими. Вони викликають порушення правильності гратки, що поширюється на відстані порядку декількох періодів.

Крім точкових, існують дефекти, зосереджені поблизу деяких ліній. Їх називають лінійними або дислокаціями. Дефекти такого виду порушують правильне чергування кристалічних площин. Найпростішими видами дислокації є крива і гвинтова дислокації.

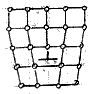
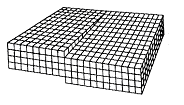
Крайова дислокація обумовлена зайвою кристалічною півплощиною, всунутою між двома сусідніми шарами атомів. Край цієї площини утворює дислокацію даного виду. Лінією дислокації є перпендикуляр по площині малюнка пряма.

Гвинтову дислокацію можна представити як результат розрізу кристалу по півплощині і наступного зсуву частин гратки, що лежать по різні боки розрізу, назустріч одна одній на величину одного періоду.

Внутрішній край розрізу утворює гвинтову дислокацію (пунктирна лінія). Кристал з гвинтовою дислокацією фактично складається з однієї кристалічної площини, яка зігнута по гвинтовій поверхні (гелікоїд). Лінія дислокації співпадає з віссю гвинта. При кожному обході навколо цієї лінії кристалічна площина зміщується на один період.

5.Теплоємність – відношення кількості теплоти, яка отримана тілом при нескінченно малій зміні його температури до цієї зміни:

. (7)

Теплоємність тіла залежить від його хімічного складу, маси, термодинамічного стану і від виду процесу зміни стану тіла при наданні йому кількості теплоти 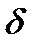Q.

Для однорідних тіл краще користуватися поняттям питомої та мольної теплоємності.

Під питомою теплоємністю розуміють теплоємність одиниці маси речовини:

. (8)

Молярна – теплоємність 1 моля речовини:

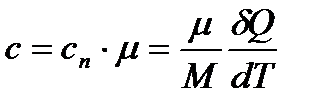. (9)

На основі рівнянь (1.2.7) і (1.2.9), кількість теплоти, яка надана тілу при зміні його температури на величину dT:

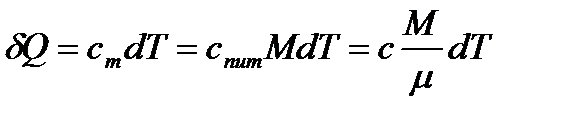. (10)

Залежність теплоємності від виду процесу зміни стану в системі детальніше розглянемо при вивченні ізопроцесів ідеального газу.

7.Ентальпія

Для процесів, які протікають при постійному тискові (p=const), перший закон термодинаміки можна записати у вигляді:

,

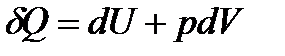або:

.

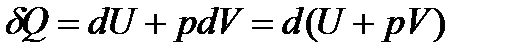Величина (U+pV) дорівнює H:

U+pV=H, (15)

і це є функція зміни стану, яка називається ентальпією. Використовуючи цю функцію, знаходимо, що кількість теплоти, отриманої тілом в ході ізобарного процесу, чисельно дорівнює:

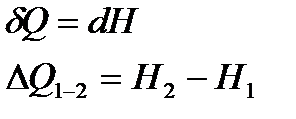. (16)

Якщо продиференціювати рівняння (15) з урахуванням другого закону термодинаміки 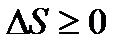, то отримаємо:

dH=dU+pdV+Vdp=TdS-pdV+pdV+Vdp=TdS+Vdp.

Звідси витікає, що ентальпія – термодинамічна функція змінних ентропії і тиску. Її частинні похідні:

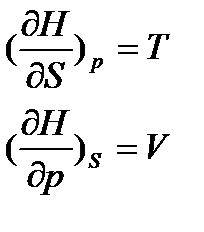. (17)

З урахуванням (16), теплоємність при p=const:

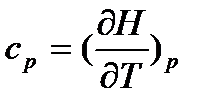(18)

Співставляючи властивості внутрішньої енергії і ентальпії, неважко зрозуміти, що при p=const ентальпія володіє властивостями, аналогічними до тих, що має внутрішня енергія при V=vonst.

8.І закон термодинаміки

.

.

.

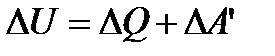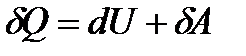За першим законом термодинаміки: теплота, надана системі витрачається на зміну внутрішньої енергії системи і на здійснення системою роботи проти зовнішніх сил.

Перший початок термодинаміки стверджує: неможливий процес, єдиним результатом якого було б виконання роботи без яких-небудь змін в інших тілах. Іншими словами, неможливий вічний двигун першого роду.

Дата добавления: 2015-05-26