Ентропія та її властивості

Ентропія – S – універсальна міра різних форм руху матерії.

Ентропія – функція стану, тобто:

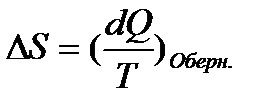. (8)

З даного рівняння можна побачити, що dU і dS мають однаковий знак, звідки випливає, що по характеру зміни ентропії системи можна казати про напрям процесу теплообміну (при нагріванні тіла ентропія збільшується, при охолодженні - зменшується).

Ентропія системи тіл дорівнює сумі ентропій усіх тіл, що входять в дану систему.

,

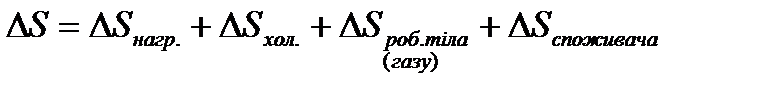дорівнює нулю, бо система повертається в початкове положення

дорівнює нулю, бо споживач отримує енергії. Тільки у формі роботи.

Зміна ентропії даної системи:

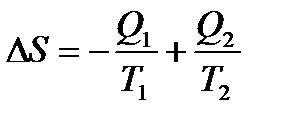. (9)

Тоді:

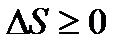. (10)

Формулювання даного твердження: ентропія замкненої системи при будь-яких процесах, що в ній відбуваються, не може зменшуватись. У випадку обернених процесів вона залишається незмінною, а у випадку необернених процесів – збільшується:

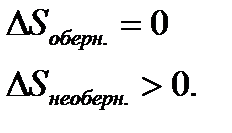
З означення ентропії , для обернених процесів:

,

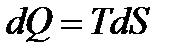а для необернених процесів:

.

Тоді:

.

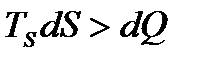З урахуванням даного рівняння, перший закон термодинаміки можна записати у вигляді:

.

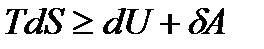3.Основне рівняння МКТ газів

Для ідеального газу розмірами молекул та зіткненнями між ними можна знехтувати. Потрібно враховувати зіткнення молекул зі стінками посудини.

Нехай газ знаходиться в посудині, що має форму прямокутного паралелепіпеда, стінки якого ідеально-відображаючі:

Розрахуємо тиск газу на стінку з площею S. При зіткненні молекули газу зі стінкою посудини, зміниться складова, що перпендикулярна до грані. Відповідна зміна імпульсу молекули при одиничному зіткненні її зі стінками:

.

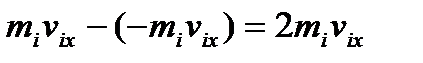За одиницю часу молекула здійснює z таких ударів:

,

- середній час,за який молекула здійснює 1 удар:

,

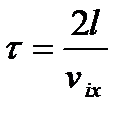тоді:

.

Відповідно з 2 і 3 законами Ньютона, результуюча сила, що діє на стінку зі сторони N молекул газу, що знаходяться в посудині дорівнює половині зміни імпульсу:

. (14)

Тиск газу на грань, яка розглядається, визначається як відношення сили, що діє на грань на площу S грані:

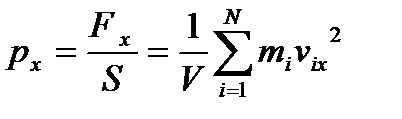, (15)

V – об’єм, який займає даний газ.

Значення дії тиску на інші грані:

(16)

Так як в стані термодинамічної рівноваги газу рух молекул у всіх напрямках буде рівномірним, то:

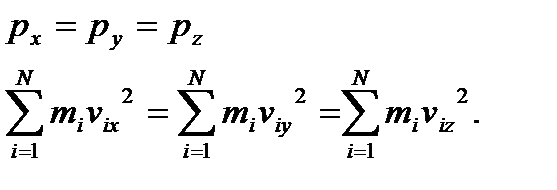
Згідно з теоремою Піфагора:

,

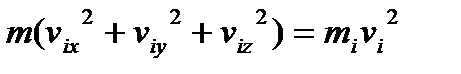тоді можна записати:

.

Для кожної з цих складових:

,

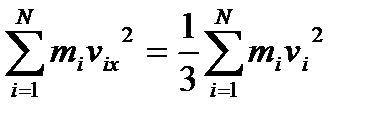тому тиск газу на стінки посудини визначається за формулою:

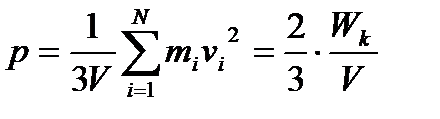, (17)

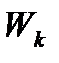- кінетична енергія усіх молекул газу.

Для однорідного газу маса усіх молекул однакова, а швидкості – різні, тому рівняння для тиску:

, (18)

n - концентрація молекул в одиниці об’єму.

Рівняння (17) і (18) використовуються в релятивістському і нерелятивістському русі, але в релятивістському русі необхідно враховувати залежність маси від швидкості руху.

4. Ізобарний

Ізобарний процес відбувається в системі при сталому тиску (P=const).

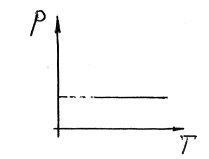
Такий процес можна здійснити, коли газ, наприклад, міститься в циліндрі з рухомим поршнем. Зміна температури газу в такому циліндрі зумовлює переміщення поршня, тобто зміну об’єму. Тиск при цьому залишається сталим:

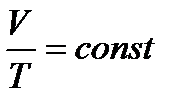. (22)

Це рівняння ізобарного процесу, виражає закон Гей-Люссака:

,

- коефіцієнт об’ємного розширення газу, = 0,003661 .

Аналогічно, коефіцієнт χ:

.

Розглянемо графік p(V): газ, поміщений в циліндр із вільно-рухомим поршнем, під час нагрівання 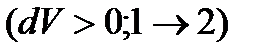або під час охолодження здійснює ізобарний процес.

Елементарна робота:

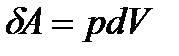(23)

є повним диференціалом деякої функції. Оскільки p=const, то робота є однозначною функцією параметрів початкового і кінцевого станів системи (параметр V). Звідси:

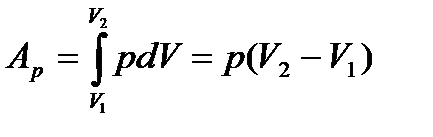. (24)

Диференціюючи рівняння Менделєєва-Клайперона при сталому тиску, одержимо:

,

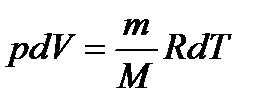тоді:

.

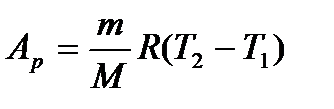Кількість теплоти, якою газ обмінюється в ізобарному процесі при незалежності 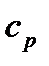від температури:

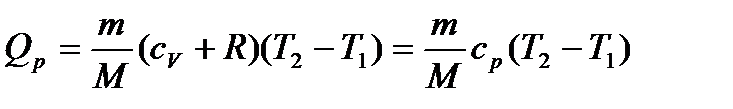. (25)

Кількість теплоти 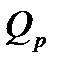йде не тільки на збереження внутрішньої енергії, а й на виконання роботи щодо розширення газу:

(26)

7. Будова рідини

Рідина – проміжний стан між кристалом і газом. Має проміжні риси:

- наявність певного об’єму;

- рідина приймає форму наданої посудини;

- у відношенні характеру розташування частинок спостерігається ближній порядок.

Тобто по відношенню до будь-якої частинки розташування найближчих сусідів є впорядкованим. Проте по мірі віддалення від даної частинки розташування по відношенню до неї інших частинок стає все менш впорядкованим і доволі швидко порядок в розташуванні частинок зникає.

Наявність в рідинах ближнього порядку є причиною того, що структуру рідин називають квазікристалічною.

Через відсутність дальнього порядку рідини, за деякими виключеннями не виявляють анізотропію.

В рідинах з продовженими молекулами спостерігається однакова орієнтація молекул в межах значного об’єму. Такі рідини отримали назву рідких кристалів.

Згідно Френкелю, тепловий рух в рідинах має наступний характер: кожна молекула протягом деякого часу коливається навколо певного положення рівноваги. Час від часу молекула змінює місце рівноваги, скачком переміщуючись у нове положення, що відстає від попереднього на відстань порядку розмірів самої молекули. Таким чином молекули повільно переміщуються всередині рідини, перебуваючи частину часу біля певних місць.

8. Рівняння Клайперона-Клаузіуса

Розглянемо цикл Карно для системи, що складається з двох фаз даної речовини, які знаходяться у рівновазі.

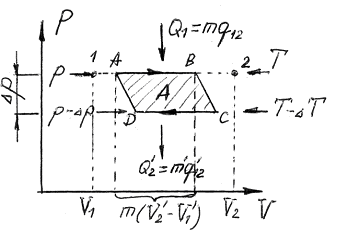
1, 2 – крайні точки горизонтальної ділянки ізотерми з температурою Т.

Стани 1 і 2 – однофазні. Всі проміжні стани відрізка 1-2 – двофазні, що відрізняються розподілом маси речовини між 1-ю і 2-ю фазами.

Ізотермічний процес супроводжується фазовим перетворенням деякої маси речовини m. При цьому об’єм речовини отримує приріст:

,

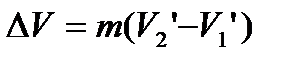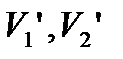- питомі об’єми 1-ої і 2-ої фаз.

Для того, щоб такий приріст міг відбутися, речовині потрібно надати кількість теплоти:

,

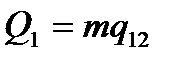- питома теплота, що поглинається при переході з стану 1 в 2 при температурі Т;

- тепло, яке отримує система в ході циклу від нагрівача.

Холодильнику тепло віддається в ході процесу :

,

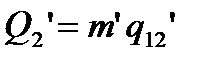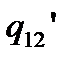- теплота переходу 1-2 при температурі ;

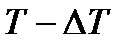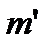- маса речовини, що переносить фазові перетворення в ході процесу . .

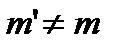На ізотермічній ділянці А-В ентропія системи отримує приріст:

.

На ізотермічній ділянці CD:

.

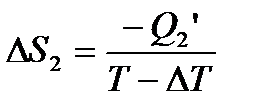В ході адіабатичних процесів B-C і D-A ентропія не змінюється.

Повний приріст ентропії за цикл дорівнює нулю. Отже:

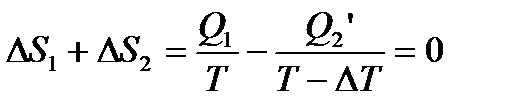
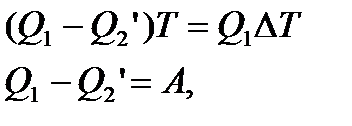
А – робота, що здійснюється за цикл. Вона приблизно дорівнює площі циклу.

.

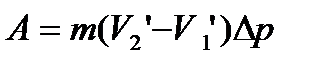Таким чином:

Звідси:

.

При 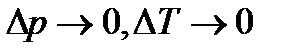рівність стане строгою:

.

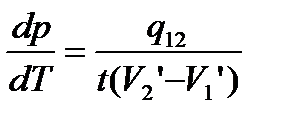Це рівняння – рівняння Клайперона-Клаузіуса.

1.

Адіабатичний

Адіабатичний процес відбувається без теплообміну з навколишнім середовищем.

Адіабатне розширення або стискання газу можна здійснити, помістивши його в циліндр із нетеплопровідними стінками і поршнем, і досить повільно переміщуючи поршень назовні або всередину циліндра. Стан системи при адіабатичному процесі можна змінити тільки за допомогою зміни зовнішніх параметрів.

Для цього процесу характерним є те, що газ увесь час залишається під зовнішнім тиском, який дорівнює пружності газу. Другою умовою адіабатичного процесу є теплоізольованість газу від навколишнього середовища.

Для адіабатичного процесу рівняння першого закону термодинаміки має вигляд:

. (30)

Виразимо P через V і T з рівняння стану ідеального газу:

.

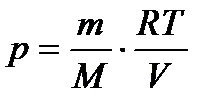Підставимо в попереднє рівняння і скоротимо на відмінний від нуля множник :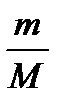

.

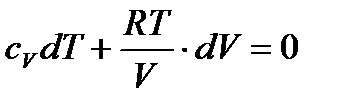Розділимо обидві частини рівняння на :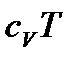

.

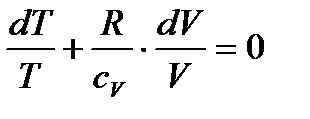Це співвідношення можемо записати у вигляді:

,

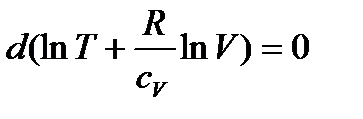звідси слідує, що при адіабатичному процесі:

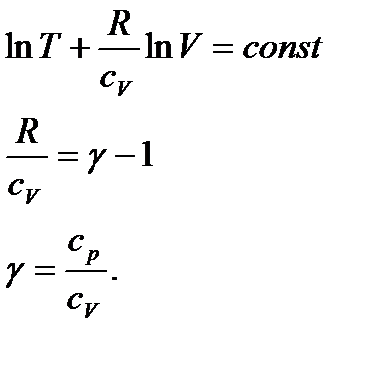
Проінтегрувавши і підставивши, одержимо:

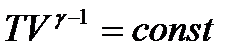. (31)

Це рівняння адіабатичного газу в змінних T і V:

,

враховуючи, що величини M,m і R – сталі:

. (32)

Це рівняння адіабатичного ідеального газу в змінних P і V (рівняння Пуассона).

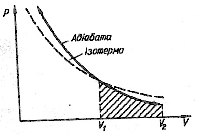
При ізотермічному процесі (pV=const), тиск газу зменшується обернено-пропорційно об’єму в першому степені. При адіабатичному розширенні тиск зменшується обернено-пропорційно . Хід адіабати крутіший порівняно з ізотермою. Фізично це пояснюється тим, що при адіабатичному розширенні зменшення тиску зумовлене не тільки збільшенням об’єму, а й зменшенням температури.

Виведемо формули для розрахунку роботи при адіабатичному процесі: з попередніх викладок для 1 моль ідеального газу:

. (33)

Оскільки

(34)

то:

,

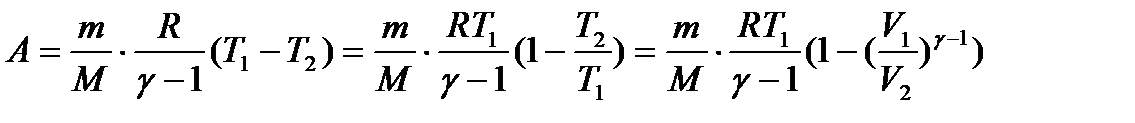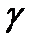- показник адіабати,

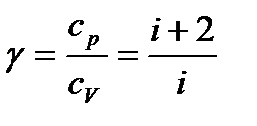. (35)

Графічно робота зображена площею заштрихованої трапеції.

2. Температура. Поняття температури

Поняття температури вводиться для характеристики різної ступені прогрітості тіл. Уявлення про температуру увійшло в науку через засоби чуттєвих сприйнять людини. Усі ці чуттєві сприйняття є суб’єктивними і неточними. В основу кількісного визначення температури покладено фізичні явища, вільні від суб’єктивізму (тепловий рух частинок, з яких складаються тіла або системи). Рух таких частинок приводить до нагрівання тіла. Рівновісність цього руху у всіх напрямках приводить до того, що макроскопічна система, представлена сама собі, приходить у стан термодинамічної рівноваги, для якого має зміст поняття температури, тобто визначення температури повинно базуватися на величині, яка б характеризувала стан тіла і яка була б однакова у будь-яких двох тіл, що знаходяться в тепловій рівновазі один з іншим. Цією властивістю володіє кінетична енергія поступального руху мікрочастинок тіла, яка вибирається мірою температури.

Розглянемо температуру газу:

з рівнянь (17) і (18) знаходимо:

,

N – число молекул:

,

,

,

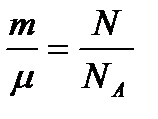k – стала Больцмана:

.

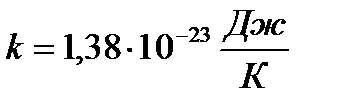Знаходимо зв’язок між температурою і середньою кінетичною енергією поступального руху його молекул:

, (19)

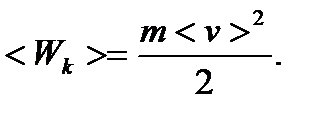
Тоді на основі рівняння (19) середня швидкість теплового поступального руху (середня квадратична швидкість) молекул газу:

, (20)

m – маса молекул.

Згідно з рівнянням (19), абсолютна температура тіла є мірою середньої кінетичної енергії поступального руху молекул. Тоді абсолютному нулю відповідає температура, при якій поступальний рух молекул зупиняється.

На основі рівняння (19) знаходимо, що температурі 1К відповідає кінетична енергія поступального руху:

~Е,

1К~ .

5.Другий закон термодинаміки

У 1924 році французький вчений Карно стверджував: будь-яка теплова машина окрім нагрівача і робочого тіла повинна мати холодильник, де температура холодильника менша за температуру нагрівача. Усі виводи Карно виражають другий закон термодинаміки.

Перше формулювання другого закону термодинаміки було сформоване у 1850 році Клаузіусом: неможливий такий процес, при якому теплота самовільно переходила б від тіл більш холодних до тіл більш нагрітих.

Незалежно від Клаузіуса, англійський фізик Томпсон у 1861 році сформулював інше формулювання: неможливий круговий процес, єдиним результатом якого було б виконання роботи за рахунок охолодження теплового резервуара (тіла або системи тіл, що знаходяться в стані термодинамічної рівноваги і володіють запасом внутрішньої енергії). Згідно з Томпсоном: вічний двигун другого роду неможливий.

Другий закон термодинаміки: ентропія замкненої системи при будь-якому реальному процесі або збільшується, або залишається незмінною ().

В стані рівноваги ентропія досягає максимуму і ніякі макропроцеси неможливі. Не дивлячись на свою загальність, другий закон термодинаміки не має абсолютного характеру і відхилення від нього є закономірним, наприклад, броунівський рух важких частинок, або рівновісне теплове випромінення великих тіл або самостійна зміна температури і тиску в рівновісній системі та інше.

.

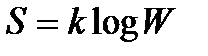Дата добавления: 2015-05-26