Ізохорний

Рівняння стану ідеального газу

Об’єм даної маси газу є функцією від p і T:

,

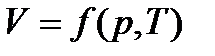тоді повний диференціал 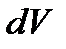визначається як похідна:

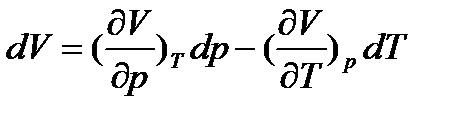. (7)

Рівняння (4) запишемо у вигляді:

,

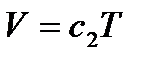тоді з рівнянь (1) і (.4):

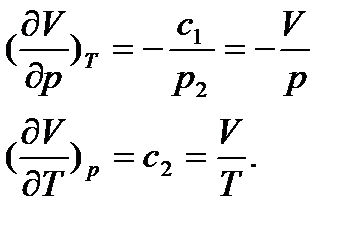(8)

Якщо підставити рівняння (8) у рівняння (7), то отримаємо:

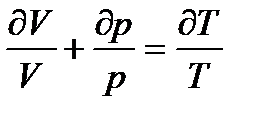. (9)

Якщо проінтегрувати, то:

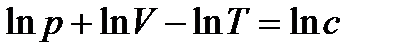. (10)

Потенціюючи дане рівняння, отримаємо:

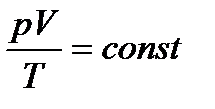. (11)

Дане рівняння було отримане французьким фізиком Клайпероном у1834році. У 1884 році Менделєєв придав рівнянню (11) універсального вигляду, записавши його для 1 моль газу з об’ємом V:

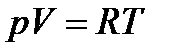, (12)

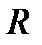- постійна величина, універсальна газова стала:

.

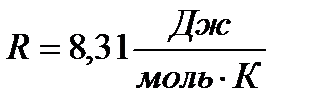Якщо помножити (12) на кількість молів 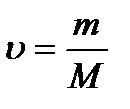, отримаємо рівняння стану ідеального газу для довільної маси:

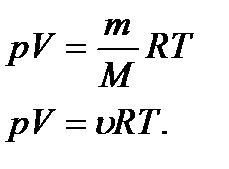(13)

Останнє рівняння – рівняння Менделєєва-Клайперона

Ізохорний процес відбувається при сталому об’ємі газу (V=const):

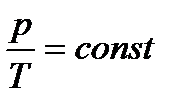. (27)

Це рівняння ізохорного процесу.

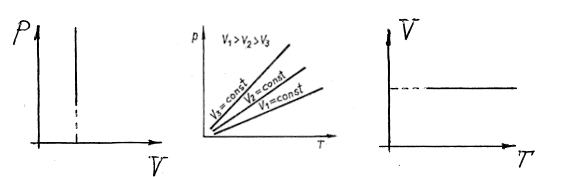
Рис. 5

За законом Шарля, рівняння ізохорного процесу також можна записувати у вигляді:

,

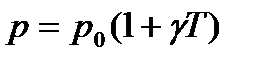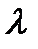- термічний коефіцієнт тиску ().

Аналогічно до коефіцієнту :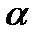

.

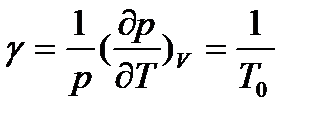Зв’язок між коефіцієнтами :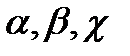

.

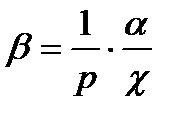Робота в ізохорному процесі дорівнює нулю:

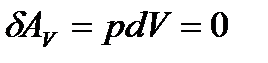(28)

.

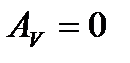Тоді рівняння першого закону термодинаміки:

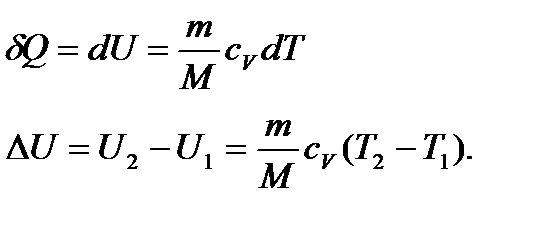(29)

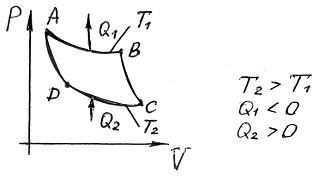
3.Обернений цикл Карно

Прямий обернений цикл Карно

Цикл Карно дозволяє підійти до поняття коефіцієнта дії теплової машини.

Схема роботи ідеальної теплової машини, що працює по циклу Карно:

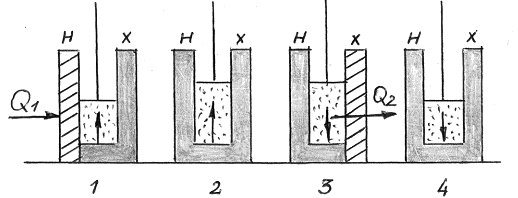
Рис. 2

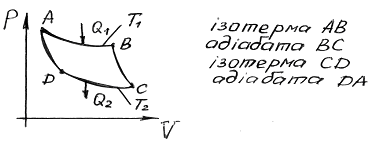
1. Нагрівач отримує теплоту , і газ під поршнем починає розширюватися так як 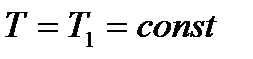(ізотерма АВ). Так як процес рівновісний, то температура газу дорівнює температурі нагрівача.

2. Газ теплоізольований і починає адіабатично розширюватись до 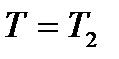яка дорівнює температурі холодильника (адіабата ВС).

3. Газ ізотермічно 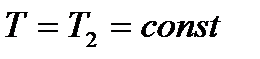стискається, віддаючи холодильнику теплоту .

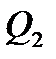4. Газ адіабатно стискається, нагріваючись до температури нагрівача (адіабата DA).

Знайдемо роботу, яку здійснює ідеальний газ в даному циклі. Так як тепловий цикл – круговий, то повна зміна внутрішньої енергії газу дорівнює нулю (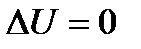). Тоді перший закон термодинаміки для робочого тіла (газу) в циклі Карно має вигляд:

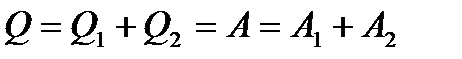, (1)

при цьому слід пам’ятати, що: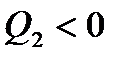

Роботу циклу можна виразити як суму робіт окремих процесів:

.

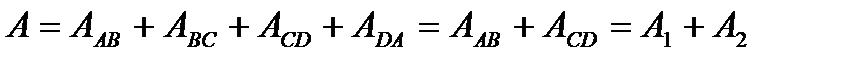Так як сумарна робота адіабатичного розширення і стискання газу в даному циклі чисельно дорівнює нулю, тому:

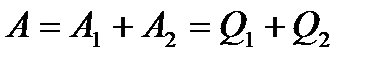, (2)

А – корисна робота циклу.

Так як 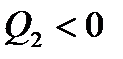, то з рівняння (2) слідує, що ця робота 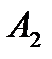і менша від тієї кількості теплоти, що підводиться до нагрівача. Частина енергії віддається холодильнику у вигляді теплоти 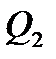. Даний висновок справедливий для будь-якого кругового процесу. Величину відношення роботи до кількості теплоти позначають 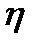- термічний коефіцієнт теплового двигуна:

.

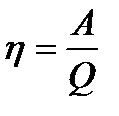Для нашого оберненого циклу Карно:

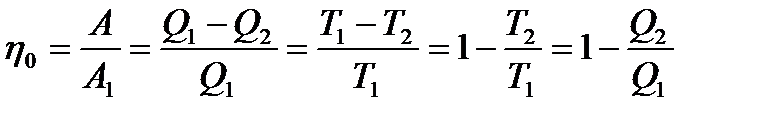. (3)

Формула (3) не має жодних даних про властивості робочого тіла і про будову теплової машини, тобто звідси випливає, що ККД усіх обернених машин, що працюють в ідеальних умовах, тобто при одній і тій самій температурі нагрівача 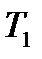і температурі холодильника 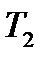буде однаковим і визначатиметься тільки температурами нагрівача і холодильника. Дане твердження носить назву теореми Карно, яка є основою встановлення термодинамічної шкали температур.

З рівняння (3) випливає:

.

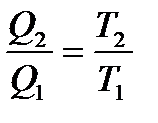Таким чином, щоб порівняти температури двох тіл 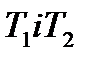, потрібно здійснити обернений цикл Карно, в якому ці тіла використовуються у вигляді нагрівача і холодильника і порівняти теплоту .

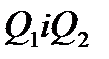Термодинамічна шкала не зв’язана з властивостями термодинамічного тіла і в цьому є її досягнення. Але внаслідок необерненості реальних термодинамічних процесів, такий спосіб порівняння температур практично не виконується і має лише принципіальне значення.

1.3.2.б. Обернений рівновісний цикл Карно

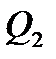В оберненому циклі Карно теплота відводиться від газу в процесі ізотермічного стискання при температурі , а кількість теплоти навпаки підводиться до газу в процесі ізотермічного розширення при 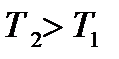. Тоді результуюча робота 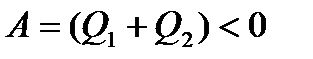, тобто результуюча робота виконується зовнішнім середовищем над газом.

Даний результат справедливий для будь-якого оберненого циклу, таким чином за рахунок здійсненої роботи зовнішніми силами над робочим тілом, можна переносити енергію у вигляді теплоти від менш нагрітого тіла до більш нагрітого тіла. Даний метод використовується в холодильній техніці. Холодильна техніка буде тим більш економічною, чим менша буде робота 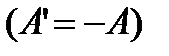, яка витрачається зовні на відведення від холодильного тіла теплоти .

З рівняння, що і з умови, що 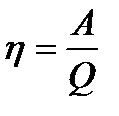, знаходимо, що:

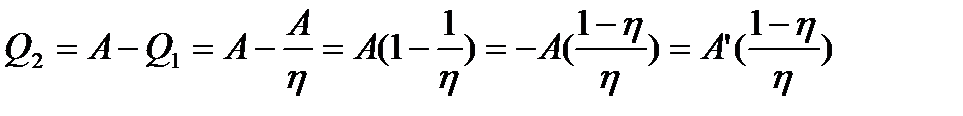. (4)

4.Потенціал Гіббса

Енергією Гіббса називається функція стану, що визначається рівнянням:

G=H-TS=U+pV-TS. (19)

Повний диференціал енергії Гіббса визначається як:

.

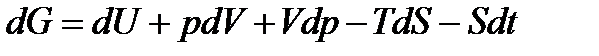Така як dU=TdS-pdV, то потенціал енергії Гіббса:

dG=Vdp-SdT.

Тобто природними змінними для функції енергії Гіббса є тиск і температура (p i T), а частинні похідні цієї функції:

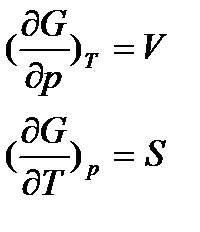. (20)

Якщо температура T і тиск p залишаються сталими, то відповідно до рівняння (13) можна записати:

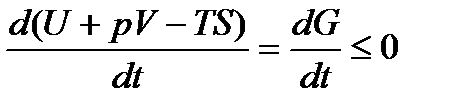. (21)

З рівняння слідує: якщо необхідний процес буде проходити при постійному тискові p=const і постійній температурі T=const, то це буде супроводжуватися зменшенням енергії Гіббса.

В стані рівноваги енергія Гіббса буде мінімальною.

Дата добавления: 2015-05-26