Подбор параметров линейной зависимости. Линия регрессии. Коэффициент корреляции

AОбработка результатов эксперимента методом наименьших квадратов. Реализация МНК в MathCAD.

Пусть в результате эксперимента были получены некоторые данные, представленные в виде таблицы.

x	x 0	x 1	x 2	x 3	x 4	x 5	x 6	…	xn- 1
y	y 0	y 1	y 2	y3	y4	y 5	y 6	…	yn- 1

Необходимо построить аналитическую зависимость, наиболее близко описывающую результаты эксперимента.

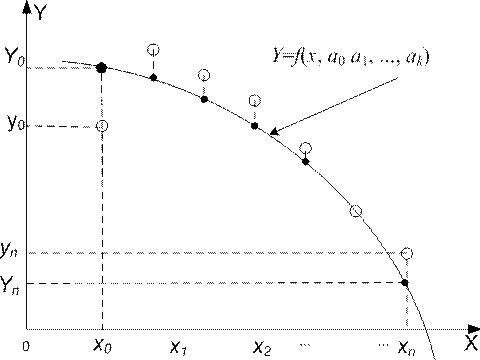
Идея метода наименьших квадратов заключается в том, что функцию

Y = f (x, a ₀ a ₁,..., a_k)

необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений y _i от расчетных Y_i была наименьшей:

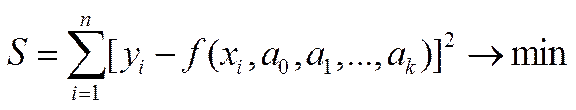(1)

Т.о., задача сводится к определению коэффициентов a_i

Пусть необходимо определить параметры функции, описывающей линейную зависимость:

y = a ₀ + a ₁ x.

Дано: количество экспериментальных данных n;

координаты экспериментальных точек x_i и y_i (i =0, n -1).

Найти: коэффициенты a ₀ и a ₁.

Линия, описываемая уравнением вида y = a ₀ + a ₁ x, называется линией регрессии y на x.

Параметры a ₀ и a ₁ называются коэффициентами регрессии и определяются формулами:

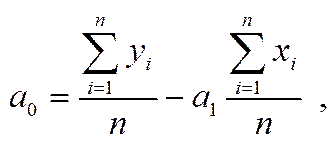(2)

(3)

Формулы (2) и (3) получены из условия (1): чем меньше величина:

тем более обоснованно предположение, что экспериментальные данные описываются линейной функцией.

Существует показатель, характеризующий тесноту линейной связи между x и y, называемый коэффициентом корреляции и рассчитываемый по формуле:

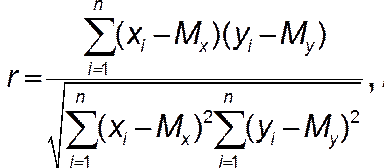
где

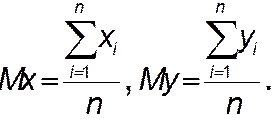(4)

Значение коэффициента корреляции удовлетворяет соотношению:

–1 £ r £ 1.

Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки.

Если коэффициент корреляции равен нулю, то это означает, что между x и y не существует линейной связи, но между ними может существовать зависимость, отличная от линейной.

1.1. Вычисление коэффициентов регрессии в MathCAD.

Для определения коэффициентов линии регрессии

y = a ₀,+ a ₁ x

в MathCAD существуют следующие функции:

line(x,y) – возвращает массив

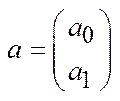
коэффициентов регрессии;

intercept(x,y) – возвращает коэффициент регрессии a₀;

slope(x,y) – возвращает коэффициент регрессии a₁.

Здесь

x – массив абсцисс экспериментальных точек,

y – массив ординат экспериментальных точек.

ЗАДАЧА 1. Для заданных экспериментальных данных вычислить коэффициенты регрессии. В одной графической области изобразить экспериментальные данные и линию регрессии. Найти значение линии регрессии в точке х=50.

Решение.

1. Ввод экспериментальных данных: количество точек n; массив абсцисс х; массив ординат y. Массив задается как вектор-столбец.

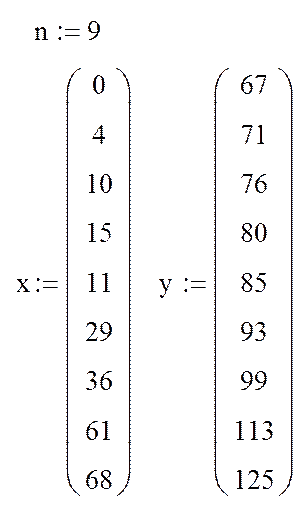
2. Вычисление коэффициентов регрессии а:

3. Определение линии регрессии:

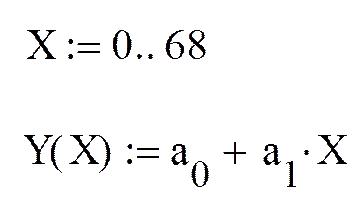
Здесь X иY – теоретические значения линии регрессии.

4. Построение в одной графической области экспериментальных точек и линии регрессии:

5. Вычисление значения функции в точке:

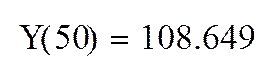
1.2. Вычисление коэффициента корреляции в MathCAD.

Для вычисления коэффициента корреляции в MathCAD предназначена функция

corr(x,y)

где x и y – массивы экспериментальных точек.

Например, для задачи 1:

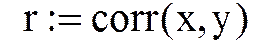
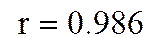
1.3. Функции, приводимые к линейной

Функция	Преобразование
Y = ax^b	ln(y)=ln(ax^b)= ln(a)+ b ln(x) Y =ln(y), X =ln(x), A =ln(a) Y = A + bX, где a = e^A
Y = ae^bx	ln(y) = ln(a) + bx ln(e) Þ ln(y) = ln(a) + bx. Y =ln(y), A =ln(a) Y = bx + A, где a = e^A.

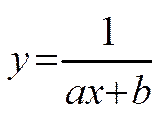
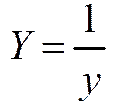
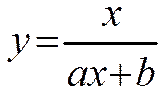
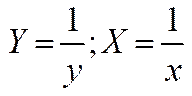
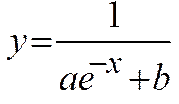
Дата добавления: 2015-05-26