Подбор параметров нелинейной зависимости. Вычисление индекса корреляции

2.1. Полные полиномы.

Пусть необходимо определить параметры функции:

Y = a ₀ + a ₁ x + a ₂ x ².

Это многочлен второй степени.

Составим функцию (1):

.

Исходя из того, что эта функция должна быть наименьшей, получим:

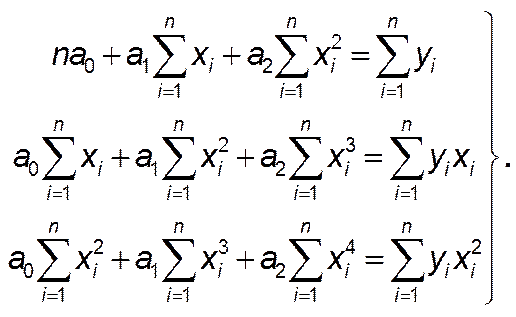(5)

Решив систему (5), найдем значение параметров a _o, a ₁, a ₂.

Для определения параметров многочлена третьей степени

Y = a _o + a ₁ x + a ₂ x ² + a ₃ x ³.

Составим функцию (1):

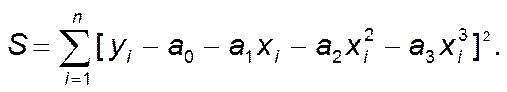и получим систему для вычисления параметров a _o, a ₁, a ₂, a ₃:

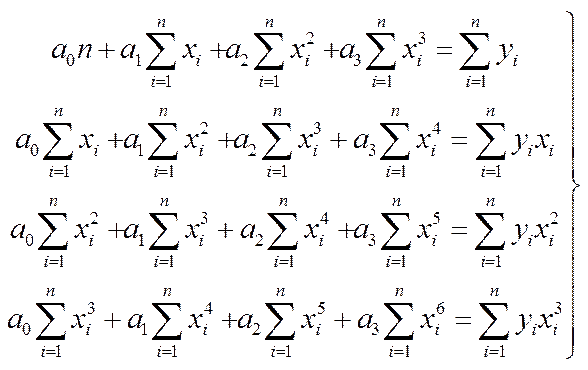(6)

Аналогично можно найти параметры многочлена k -й степени:

Y = a ₀ + a ₁ x + a ₁ x ² +... + a_k x^k

Коэффициенты полного полинома любой степени можно подобрать c помощью функций:

regress(x,y,k) – возвращает вектор коэффициентов полинома k-й степени, подобранного методом наименьших квадратов по экспериментальным точкам; здесь x – массив абсцисс (должен быть упорядочен по возрастанию), y – массив ординат экспериментальных точек.

interp(s,x,y,t) – вычисляет значения полинома в точке t; x – массив абсцисс, y – ординат экспериментальных точек, s – массив коэффициентов, найденный с помощью функции regress (первые три элемента этого массива - специальные значения, используемые функцией interp, последующие элементы - коэффициентами подобранного полинома).

ЗАДАЧА 2. Для заданных экспериментальных данных построить аппроксимирующие зависимости:

,

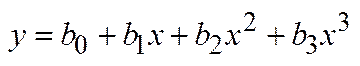
Решение.

1. Ввод экспериментальных данных.

2. Вычисление коэффициентов полинома второй степени:

3. Определение функции и построение графика:

4. Вычисление коэффициентов полинома третьей степени:

5. Вычисление значений полинома в заданных точках (определение теоретических значений)

6. Построение графика:

7. Построение двух графиков в одной графической области:

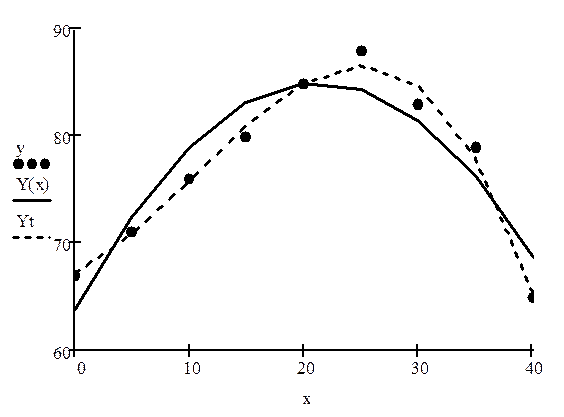
2.2. Подбор параметров любой нелинейной функции.

Для подбора параметров функции вида:

,

где – любые известные функции, используют функцию

linfit (x,y,F).

где x – массив абсцисс, y – массив ординат экспериментальных точек, F– вектор, содержащий функции в символьном виде.

Функция linfit возвращает вектор коэффициентов K.

ЗАДАЧА 3. Известна табличная зависимость z от t. Аппроксимировать эту зависимость методом наименьших квадратов с помощью функций

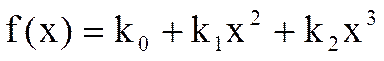
1. Ввод исходных данных:

2. Определение :

3. Вычисление коэффициентов k_i:

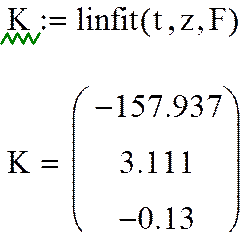
4. Определение теоретических значений:

5. Построение графика

2.3. Подбор параметров функции y = ax^be^cx

Прологарифмируем выражение

Y = ax^be^cx:

ln (y)= ln (a) + b ln (x) + cx ln (e)

и сделаем замену

Y = ln(y), A = ln(a):

Y = A + b ln (x) + cx.

Например, аппроксимация этой функцией экспериментальных данных из задачи 3 будет иметь вид:

2.4. Криволинейная корреляция

Коэффициент корреляции r применяется только в тех случаях, когда между данными существует прямолинейная связь. Если же связь криволинейная, то пользуются индексом корреляции, который рассчитывается по формуле:

(7)

где

y – экспериментальные значения,

Y – теоретические значения,

M_y – среднее значение y.

Индекс корреляции по своему абсолютному значению колеблется в пределах от 0 до 1. При функциональной зависимости индекс корреляции равен 1. При отсутствии связи R = 0.

Если коэффициент корреляции r является мерой тесноты связи только для линейной формы связи, то индекс корреляции R – и для линейной, и для криволинейной.

При прямолинейной связи коэффициент корреляции по своей абсолютной величине равен индексу корреляции:

ЗАДАЧА 4. Вычислить индекс корреляции для данных из задачи 3.

z – экспериментальное значение функциии;

Z(t) – теоретическое значение функциии;

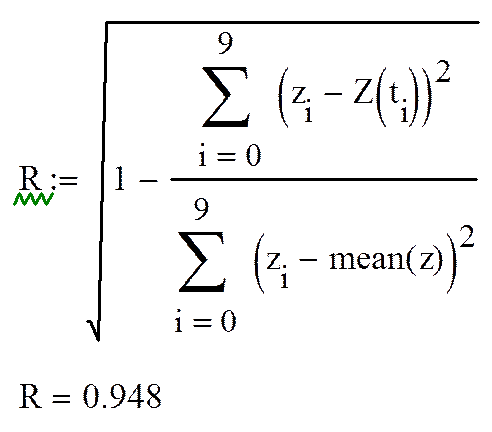
2.5. Вычисление суммарной ошибки

Суммарная ошибка это сумма квадратов отклонений измеренных значений y _i от расчетных Y_i. Вычисляется по формуле:

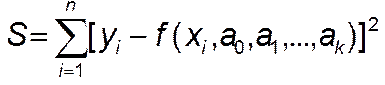
ЗАДАЧА 5. Вычислить суммарные ошибки для функций, вычисленных в задаче 2.

1. Суммарная ошибка для полинома второй степени:

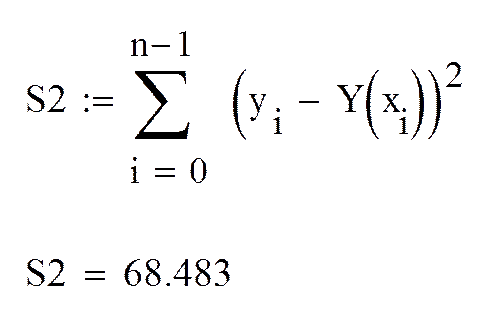
2. Суммарная ошибка для полинома третьей степени:

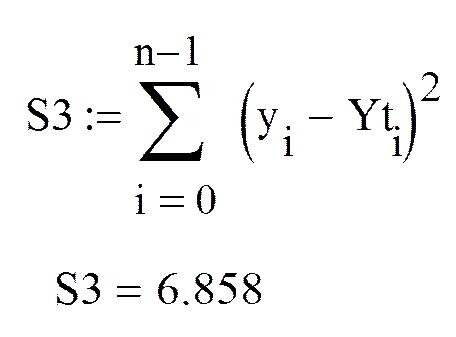
Дата добавления: 2015-05-26