Непараметрические критерии

Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия. Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.

Критерий знаков (G-критерий)

Критерий предназначен для срав­нения состояния некоторого свойства у членов двух зави­симых выборок на основе измерений, сделанных по шка­ле не ниже ранговой.

Имеется две серии наблюдений над случайными переменными X и У, полученные при рассмотрении двух зависимых выборок. На их основе составлено N пар вида (х_i, у_i), где х_i, у_i — результаты двукратного измерения одного и того же свойства у одного и того же объекта.

В педагогических исследованиях объектами изуче­ния могут служить учащиеся, учителя, администрация школ. При этом х_i, у_i могут быть, например, балловы­ми оценками, выставленными учителем за двукратное выполнение одной и той же или различных работ одной и той же группой учащихся до и после применения некоторого педагогическою средства.

Элементы каждой пары х_i, у_i сравниваются между собой по величине, и паре присваивается знак «+», ес­ли х_i < у_i, знак «—», если х_i > у_i и «0», если х_i = у_i.

Нулевая гипотеза формулируются следующим обра­зом: в состоянии изучаемого свойства нет значимых различий при первичном и вторичном измерениях. Альтернативная гипотеза: законы распределения величин X и У различны, т. е. состояния изучаемого свойства существенно раз­личны в одной и той же совокупности при первичном и вторичном измерениях этого свойства.

Ста­тистика критерия (Т) определяется следую­щим образом:

допустим, что из N пар (х, у,) нашлось несколько пар, в которых значения х_i и у_i равны. Такие пары обозначаются знаком «0» и при подсчете значения ве­личины Т не учитываются. Предположим, что за вы­четом из числа N числа пар, обозначенных знаком «0», осталось всего n пар. Среди оставшихся n пар подсчита­ем число пар, обозначенных знаком «-», т.е, пары, в которых x_i<y_i. Значение величины Т и равно чис­лу пар со знаком минус.

Нулевая гипотеза принимается на уровне значимости 0,05, если наблю­даемое значение T<n-t_a, где значение n-t_a определя­ется из статистических таблиц для критерия знаковПриложения 2.

Пример 4. Учащиеся выполняли контрольную ра­боту, направленную на проверку усвоения некоторого понятия. Пятнадцати учащимся затем предложили электронное пособие, составленное с целью фор­мирования данного понятия у учащихся с низким уров­нем обучаемости. После изучения пособия учащиеся снова выполняли ту же контрольного работу, которая оценивалась по пятибалльной системе.

Результаты двукратного выполнения ра­боты представляют измерения по шкале по­рядка (пятибалльная шкала). В этих условиях возмож­но применение знакового критерия для выявления тенденции изменения состояния знаний учащихся после изучения пособия, так как выполняются все допуще­ния этого критерия.

Результаты двукратного выполнения работы (в бал­лах) 15 учащимися запишем в форме таблицы (см. табл. 1).

Таблица 4.

Учащиеся (№)

Первое выполнение

Второе выполнение

Знак разности отметок

+

+

+

+

-

+

+

+

+

-

+

+

Проверяется гипотеза H₀: состояние знаний учащих­ся не повысилось после изучения пособия. Альтернативная гипотеза: состояние знаний учащихся повысилось после изучения пособия.

Подсчитаем значение статистики критерия Т равное числу положительных разностей отметок, по­лученных учащимися. Согласно данным табл. 4 Т=10, n=12.

Для определения критических значений статистики критерия n—ta используем табл. Приложения 2. Для уровня значимости а = 0,05 при n=12 значение n—ta=9. Следовательно выполняется неравенство Т> n—ta (10>9). Поэтому в соответствии с правилом принятия решения нулевая гипотеза от­клоняется на уровне значимости 0,05 и принимает­ся альтернативная гипотеза, что позволяет сделать вывод об улучшении знаний учащихся после самостоя­тельного изучения пособия.

Пример 5. Предполагается, что изучение курса математики способствует формированию у учащихся одного из приемов логического мышления (например, приема обобщения) даже в том случае, если его фор­мирование не проводится целенаправленно. Для проверки этого предположения был проведен следующий эксперимент.

Учащимся VII класса было предложено 5 задач, решение которых основано на использовании данного приема мышления. Считалось, что учащийся владеет этим приемом, если он дает верный ответ на 3 и более задачи.

Была разработана следующая шкала измерений: верно решена 1 или 2 задачи — оценка «0»; верно решено 3 задачи — оценка «1»; верно решено 4 зада­чи— оценка «2»; верно решено 5 задач — оценка «3».

Работа проводилась дважды: в конце сентября и конце мая следующего года. Ее писали 35 одних и тех же учащихся, отобранных методом случайного отбора из 7 разных школ. Результаты двукратного выполнения работы запишем в форме таблицы (см. табл. 5).

В соответствии с целями эксперимента формулируем нулевую гипотезу следующим образом: Н₀ — изучение математики не способствует формированию изучаемого приема мышления. Тогда альтернативная гипотеза бу­дет иметь вид: Н₁ — изучение математики способствует овладению этим приемом мышления.

Таблица 5.

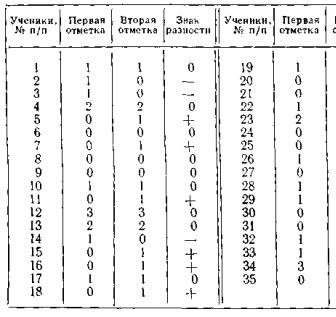Согласно данным табл. 5, значение статистики Т=15 — число разностей со зна­ком «+». Из 35 пар 12 имеют знак «0»; значит, n =35-12 = 23.

По таблице Приложения 2 для n=23 и уровня значимости 0,025 находим критическое значение стати­стики критерия, равное 16. Следовательно, верно неравенство Т<n—ta (15<16).

Поэтому в соответ­ствии с правилом принятия решений приходится сделать вывод о том, что полученные ре­зультаты не дают достаточных оснований для отклоне­ния нулевой гипотезы, т. е. мы не располагаем достаточными основаниями для отклонения утверждения о том, что изучение математики само по себе не способ­ствует овладению выделенным приемом мышления.

Критерий χ2 (хи-квадрат)

Критерий χ² (хи-квадрат) приме­няется для сравнения распределений объектов двух совокупностей на основе измерений по шкале наименований в двух независимых выборках.

Предполо­жим, что состояние изучаемого свойства (например, вы­полнение определенного задания) измеряется у каждо­го объекта по шкале наименований, имеющей только две взаимоисключающие категории (например: выпол­нено верно — выполнено неверно). По результатам из­мерения состояния изучаемого свойства у объектов двух выборок составляется четырехклеточная таблица 2X2. (см. табл. 6).

Таблица 6.

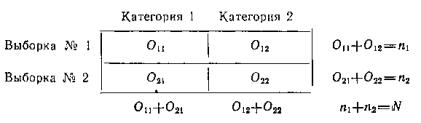
В этой таблице О_ij — число объектов в i -ой выбор­ке, попавших в j -ую категорию по состоянию изучае­мого свойства; i=1,2 – число выборок; j=1,2 – число категорий;; N — общее число наблюдений, равное О₁₁ + О₁₂ + О₂₁ + О₂₂ или n₁+n₂.

Тогда на основе данных таблицы 2X2 (см. табл. 6) можно проверить ну­левую гипотезу о равенстве вероятностей попадания объектов первой и второй совокупностей в первою (вторую) категорию шкалы измерения проверяемого свойства, например гипотезу о равенстве вероятностей вер­ного выполнения некоторого задания учащимися кон­трольных и экспериментальных классов.

При проверке нулевых гипотез не обязательно, чтобы значения вероятностей р₁ и р₂ были известны, так как гипотезы только устанавливают между ними неко­торые соотношения (равенство, больше или меньше).

Для проверки рассмотренных выше нулевых гипотез по данным таблицы 2X2 (см. табл. 6) подсчитывается значение статистики критерия Т по следующей общей формуле:

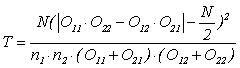(9)

где n₁, n₂ — объемы выборок, N = n₁ + n₂ — общее число наблюдений.

Проводится проверка гипотезы H₀: p₁£p₂ — при альтернативе Н₁: р₁>р₂. Пусть a — принятый уровень значимости. Тогда значение статистики Т, полученное на основе экспериментальных данных, сравнивается с критическим значением статистики х_1-2a,, которое опре­деляется по таблице c² c одной степенью свободы (см. Приложение 2) с учетом выбранного значения a. Если верно неравенство T<x_1-2a, то нулевая гипотеза принимается на уровне a. Если данное неравенство не выполняется, то у нас нет достаточных оснований для отклонения нулевой гипотезы.

В связи с тем что замена точного распределения статистики Т распределением c² c одной степенью сво­боды дает достаточно хорошее приближение только для больших выборок, применение критерия ограничено не­которыми условиями.

Критерий не рекомендуется использовать, если:

1) сумма объемов двух выборок меньше 20;

2) хотя бы одна из абсолютных частот в таблице 2X2, составленной на основе экспериментальных данных, меньше 5.

Пример 6. Проводился эксперимент, направленный на выявление лучшего из учебников, написанных двумя авторскими коллективами в соответствии с целями обу­чения геометрии и содержанием программы IX класса. Для проведения эксперимента методом случайного отбо­ра были выбраны два района, большинство школ которых относились по расположению к сельским. Уча­щиеся первого района (20 классов) обучались по учеб­нику № 1, учащиеся второго района (15 классов) обуча­лись по учебнику №2.

Рассмотрим методику сравнения ответов учителей экспериментальных школ двух районов па один из вопросов анкеты: «Доступен ли учебник в целом для самостоятельного чтения и помогает ли он усвоить материал, который учитель не объяснял в классе (Ответ: да — нет.)

Отношение учителей к изучаемому свойству учебников измерено по шкале наименований, имеющей две категории: да, нет. Обе выборки учителей случайные и независимые.

Ответы 20 учителей первого района и 15 учителей второго района распределим на две категории и запишем в форме таблицы 2Х2 (табл. 5).

Таблица 7.

Все значения в табл. 7 не меньше 5, поэтому в соответствии с условиями использования критерия c² подсчет статистики критерия производится по формуле (9).

По таблице из приложения 2для одной степени свободы (v=l) и уровня значимости a=0,05 найдем х_1-aа =Т_критич = 3,84. Отсюда верно неравенство Т_наблюд<Т_критич (1,86<3,84). Согласно правилу принятия ре­шений для критерия c², полученный результат не дает достаточных оснований для отклонения нулевой ги­потезы, т. е. результаты проведенного опроса учителей двух экспериментальных районов не дают достаточных оснований для отклонения предположения об одинаковой доступности учебников № 1и 2 для самостоятельного чтения учащимися.

Применение критерия хи-квадрат возможно и в том случае, когда объекты двух выборок из двух совокупно­стей по состоянию изучаемого свойства распределяют­ся более чем на две категории. Например, учащиеся экспериментальных и контрольных классов распределя­ются на четыре категории в соответствии с отметками (в баллах: 2, 3, 4, 5), полученными учащимися за вы­полнение некоторой контрольной работы.

Результаты измерения состояния изу­чаемого свойства у объектов каждой выборки распре­деляются на С категорий. На основе этих данных со­ставляется таблица 2ХС, в которой два ряда (по числу рассматриваемых совокупностей) и С колонок (по чис­лу различных категорий состояния изучаемого свойства, принятых в исследовании).

Таблица 8.

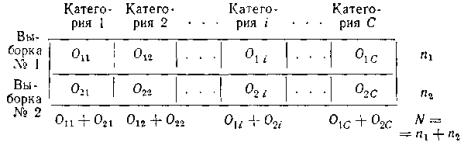
На основе данных таблицы 8 можно проверить нулевую гипотезу о равенстве вероятностей попадания объектов первой и второй совокупностей в каждую из i (i=l, 2,..., С) категорий, т. е. проверить выполнение всех следующих равенств: р₁₁= р₂₁, p₁₂ = p₂₂, …, p_1c = p_2c. Возможна, например, проверка гипо­тезы о равенстве вероятностей получения отметок «5», «4», «3» и «2» за выполнение учащимися контрольных и экспериментальных классов некоторого задания.

Для проверки нулевой гипотезы с помощью критерия c²на основе данных таблицы 2ХС подсчитывается значение статисти­ки критерия Т по следующей формуле:

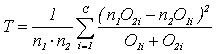(10)

где п₁ и п₂ — объемы выборок.

Значение Т, полученное на ос­нове экспериментальных данных, сравнивается с критическим значением х_1-a, которое определяется по таб­лице c² с k=С—1 степенью свободы с учетом выбранного уровня значимости a. При выполнении неравенства Т> х_1-aа нулевая гипотеза отклоняется на уровне а и принимается альтернативная гипотеза. Это означает, что распределе­ние объектов на С категорий по состоянию изучаемого свойства различно в двух рассматриваемых совокуп­ностях.

Пример 7. Рассмотрим методику сравнения результатов пись­менной работы, проверявшей усвоение одного из разде­лов курса учащимися первого и второго районов.

Методом случайного отбора из учащихся первого района, писавших работу, была составлена выборка объ­емом 50 человек, из учащихся второго района — выборка объемом 50 человек. В соответствии со специально разработанными критериями оценки выпол­нения работы каждый ученик мог попасть в одну из че­тырех категорий: плохо, посредственно, хорошо, отлично. Результаты выполнения работы двумя выборками уча­щихся используем для проверки гипотезы о том, что учеб­ник № 1 способствует лучшему усвоению проверяемого раздела курса, т. е. учащиеся первого экспериментального района в средне будут получать более высокие оценки, чем учащиеся второго района.

Результаты выполнения работы учащимися обеих вы­борок запишем в виде таблицы 2X4 (табл. 9).

Таблица 9.

В соответствии с условиями использования критерия c² подсчет статистики критерия производится по корректированной формуле (10).

=

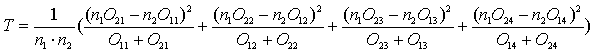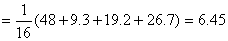
В соответствии с условиями применения двустороннего критерия хи-квадрат по таблице из приложения 2для одной степени свободы (k=4-l=3) и уровня значимости a=0,05 найдем х_1-aа =Т_критич = 7,815. Отсюда верно неравенство Т_наблюд<Т_критич (6,45<7,815). Согласно правилу принятия ре­шений для критерия c², полученный результат не дает достаточных оснований для отклонения нулевой ги­потезы.

Дата добавления: 2015-05-26