До запитання про розв‘язання алгебричних рівнянь

2.3.1 Визначення кількості дійсних коренів

Наближено визначити кількість дійсних додатних коренів алгебричного рівняння

(2.2)

можна за допомогою правила Декарта: кількість дійсних додатних коренів алгебричного рівняння 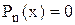із дійсними коефіцієнтами дорівнює числу змін знаку в послідовності коефіцієнтів рівняння, або на парне число менше (коефіцієнти, що дорівнюють нулю не враховуються).

Кількість від‘ємних коренів алгебричного рівняння дорівнює числу змін знаку в послідовності коефіцієнтів рівняння 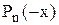або на парне число менше.

2.3.2 Визначення області існування коренів

Розглянемо два з декількох методів визначення верхньої межі додатних коренів рівняння .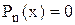

Метод Лагранжа. Якщо коефіцієнти многочлена 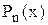відповідають умовам a₀ > 0, a₁, a₂, …,a_m-1 ≥ 0, a_m < 0, то верхня межа додатних коренів рівняння (2.2) визначається за формулою

(2.3)

де В – найбільша із абсолютних величин від‘ємних коефіцієнтів;

m – ступінь х при першому від’ємному коефіцієнті а.

Метод Ньютона. Якщо при х = С многочлен 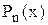і його похідні 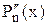, … приймають додатні значення, то С є верхньою межею додатних коренів рівняння .

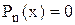Існує засіб визначення інших меж дійсних коренів з використанням методів визначення верхньої межі додатних коренів .

Якщо

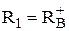рівняння ,

—″— —″— ,

—″— —″— ,

—″— —″— ,

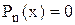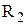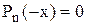то всі відмінні від нуля дійсні корені рівняння 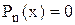(якщо вони існують) лежать у середині інтервалів

і .

Визначимо, наприклад, межі додатних і від‘ємних коренів рівняння

.

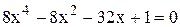Знайдемо за методом Лагранжа R₁, R₂, R₃, R₄. У многочлені 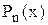a₀ = 8

> 0; а₁ = 0; а₂ = -8 < 0; a₃ = -32; a₄ = 1, m = 2. Отже, .

Для многочлена

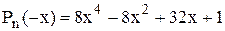
Аналогічно знаходимо .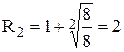

Далі, для многочлена

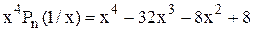
a₀ = 1 > 0; a₁ = -32 < 0, тобто m = 1, B = 32 i R₃ = 1 + 32 = 33.

Зрештою, для многочлена

Маємо a₀ = 1 > 0; a₁ = 32; a₂ = -8; a₃ = 0; a₄ = 8, тобто m = 2; B = 8. Тому .

Отже, якщо задане рівняння має дійсні корені, вони обов‘язково лежать у межах (-2; -1 / 3,828) і (1 / 33; 3).

2.3.3 Обчислення значень многочлена. Схема Горнера

Розв‘язування алгебричних рівнянь як на етапі відокремлення коренів, так і при їх уточненні потребує багаторазових обчислень значень 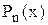. Тому важливе значення має побудова найбільш економічних (з точки зору кількості операцій) алгоритмів.

Припустимо, що треба розрахувати значення многочлена 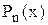(див. (2.2)) при 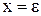. Обчислення 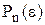вигідно проводити для перетвореного запису (2.2) до наступного вигляду

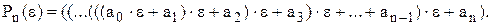(2.4)

Послідовне обчислення чисел (n множень і n додавань)

· · · · · · ·

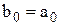
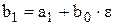
дає значення .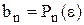

Алгоритм розрахунку 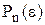, який складено на основі виразу (2.4) називають схемою Горнера. Саме у вигляді схеми розрахунки розташовують так:

+

+

+

+

+

a₀ a₁ a₂ a₃ … a_n-1 a_n

ε b₀·ε b₁·ε b₂·ε … b_n-2·ε b_n-1·ε

b₀ b₁ b₂ b₃ … b_n-1 b_n.

В першому рядку записані коефіцієнти многочлена 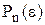. В третій рядок переносять a₀ = b₀ і далі суму добутку кожного коефіцієнта b_i на ε із а_і+1.

Дата добавления: 2015-05-26