
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 24. Основы дозиметрии 2 страница
|
|
|
|
Заключение
Ядерная физика – наука о строении, свойствах и превращениях атомного ядра – одна из самых молодых наук: ее рождение относят к 1896 г. (именно тогда А. Беккерелем была открыта радиоактивность урана). Еще в самом начале XX в. об атомном ядре ничего не было известно, и атомы считались мельчайшими неделимыми частицами материи. Однако уже к середине XX в. эта наука вышла с лабораторного на инженерный уровень развития, оказав огромнейшее влияние на всю современную цивилизацию. Достаточно вспомнить, что энергетика настоящего и, особенно, будущего уже немыслима без использования энергии атомного ядра. Управление этой энергией, решение проблем безопасности АЭС и обращения с радиоактивными отходами, а также освоение новых источников ядерной энергии требует взаимодействия специалистов самых разных профессий: физиков, математиков, инженеров, материаловедов, химиков, биологов.
С другой стороны, ядерно-физические методы находят приложение едва ли не во всех областях знания: от астрофизики до археологии. Использование источников ядерного излучения в диагностике и терапии заболеваний человека привело в последние десятилетия к выделению ядерной медицины практически в самостоятельную область знаний. Воздействие излучения на вещества, инициирующее в них химические реакции, которые не происходят в обычных условиях, дает возможность получать материалы с уникальными свойствами. Использование метода радиоактивных индикаторов в исследованиях самого разного характера (в физике, химии, биологии и т.д.) помогает получать сведения, еще недавно казавшиеся недоступными. Таким образом, можно с уверенностью сказать, что изучение основ ядерной физики сегодня необходимо уже не только самим физикам.
В заключение необходимо коснуться и теоретического аспекта ядерной физики. Не следует думать, что на все вопросы здесь уже получены ответы. Наоборот, чем глубже проникают ученые в секреты атомного ядра, тем больше загадок встает перед ними. В частности, являются ли кварки и лептоны неделимыми, то есть истинно элементарными частицами? Какие еще частицы ускользают из поля зрения исследователя микромира? Возможно ли в принципе создать полную физическую картину мира, объединяющую все частицы и их взаимодействтия?.. Ответы на эти вопросы сегодня призвана дать уже другая наука – физика элементарных частиц, или физика высоких энергий. Однако своим рождением она обязана все той же ядерной физике, начавшейся когда-то с открытия радиоактивности урана.
Рекомендуемая литература
1. Абрамов А.И., Казанский Ю.А., Матусевич Е.С. Основы экспериментальных методов ядерной физики. – М.: Атомиздат, 1977. – 528 с.
2. Балашов В.В. Строение вещества. Учеб. пособие. – М.: Изд-во МГУ, 1993. – 216 с.
3. Вальтер А.К., Залюбовский И.И. Ядерная физика. – Харьков: Основа, 1991. – 479 с.
4. Владимиров В.И. Физика ядерных реакторов: Практические задачи по их эксплуатации. – М.: Книжный дом «ЛИБРОКОМ», 2009. – 480 с.
5. Голубев Б.П. Дозиметрия и защита от ионизирующих излучений: учебник для вузов. – М.: Энергоатомиздат, 1986. – 464 с.
6. Гусев Н.Г., Климанов В.А., Машкович В.П., Суворов А.П. Защита от ионизирующих излучений: в 2 т. Т. 1. Физические основы защиты от излучений: учебник для вузов. – М.: Энергоатомиздат, 1989. – 512 с.
7. Иванов В.И. Курс дозиметрии: учебник для вузов. – М.: Энергоатомиздат, 1988. – 400 с.
8. Ишханов Б.С., Капитонов И.М., Юдин Н.П. Частицы и атомные ядра: учебник. – М.: Изд-во ЛКИ, 2007. – 584 с.
9. Матвеев А.Н. Атомная физика: Учеб. пособие для студентов вузов. – М.: Высш. шк., 1989. – 439 с.
10. Мухин К.Н. Экспериментальная ядерная физика: В 3-х тт.: Т. 1: Физика атомного ядра: учебник. – СПб.: Изд-во «Лань», 2009. – 384 с.
11. Мухин К.Н. Экспериментальная ядерная физика: В 3-х тт.: Т. 2: Физика ядерных реакций: учебник. – СПб.: Изд-во «Лань», 2009. – 326 с.
12. Мухин К.Н. Экспериментальная ядерная физика: В 3-х тт.: Т. 3: Физика элементарных частиц: учебник. – СПб.: Изд-во «Лань», 2008. – 432 с.
13. Прайс В. Регистрация ядерного излучения: пер. с англ. – М.: Изд-во иностр. лит., 1960. – 464 с.
14. Сивухин Д.В. Общий курс физики. Т. 5. Атомная и ядерная физика. – М.: Физматлит, 2002. – 784 с.
15. Старосельская-Никитина О.А. История радиоактивности и возникновения ядерной физики. – М.: Изд-во Академии Наук СССР, 1963. – 428 с.
16. Фридлендер Г.,Кеннеди Дж., Миллер Дж. Ядерная химия и радиохимия: пер. с англ. – М.: Мир, 1967. – 568 с.
17. Широков Ю.М., Юдин Н.П. Ядерная физика. – М.: Наука, 1972. – 672 с.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ А. Формула Резерфорда
Когда α-частица пролетает вблизи ядра, на нее действует кулоновская сила отталкивания
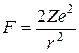 .
.
 В этом случае траектория частицы представляет собой гиперболу. Обозначим буквой θ угол между асимптотами гиперболы (рис. А), характеризующий отклонение частицы от первоначального направления (угол рассеяния). Расстояние b от ядра до первоначального направления полета α-частицы называется прицельным параметром. Чем ближе пролетает частица от ядра (чем меньше b), тем сильнее она рассеивается (тем больше θ).
В этом случае траектория частицы представляет собой гиперболу. Обозначим буквой θ угол между асимптотами гиперболы (рис. А), характеризующий отклонение частицы от первоначального направления (угол рассеяния). Расстояние b от ядра до первоначального направления полета α-частицы называется прицельным параметром. Чем ближе пролетает частица от ядра (чем меньше b), тем сильнее она рассеивается (тем больше θ).
Если считать рассеивающее атомное ядро бесконечно тяжелым, то из закона сохранения энергии следует, что вдали от ядра импульс рассеянной α-частицы р по модулю будет таким же, как и импульс до рассеяния р 0. Следовательно, модуль приращения импульса α-частицы, возникающего в результате рассеяния
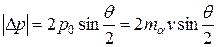 , (А.1)
, (А.1)
где v – начальная скорость частицы, mα – ее масса. Согласно 2-му закону Ньютона,
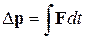 .
.
Спроектировав фигурирующие в этом равенстве векторы на направление Δ p, получим:
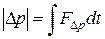 . (А.2)
. (А.2)
Из рис. A видно, что проекция силы F на направление вектора Δ p равна F cos ψ. Угол ψ можно выразить через полярный угол φ и угол рассеяния θ:
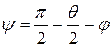 .
.
Следовательно
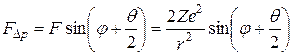 .
.
Подставим это выражение в (А.2), выразив dt как dφ / 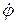 (здесь точка означает дифференцирование по времени):
(здесь точка означает дифференцирование по времени):
 . (А.3)
. (А.3)
Произведение 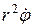 равно M / mα, где M – момент импульса α-частицы, взятый относительно рассеивающего ядра. Кулоновская сила, действующая на α-частицу, является центральной. Поэтому момент импульса остается все время постоянным и равным своему первоначальному значению mαvb. Тогда после замены
равно M / mα, где M – момент импульса α-частицы, взятый относительно рассеивающего ядра. Кулоновская сила, действующая на α-частицу, является центральной. Поэтому момент импульса остается все время постоянным и равным своему первоначальному значению mαvb. Тогда после замены 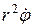 на vb интеграл (А.3) легко вычисляется:
на vb интеграл (А.3) легко вычисляется:
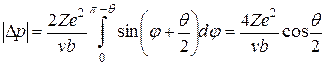 . (А.4)
. (А.4)
Сопоставляя (А.1) и (А.4), найдем, что
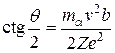 . (А.5)
. (А.5)
Рассмотрим слой рассеивающего вещества настолько тонкий, чтобы каждая α-частица при прохождении через него пролетала вблизи только одного ядра, т.е. претерпевала лишь однократное рассеяние. Чтобы рассеяться на угол, лежащий в пределах от θ до θ + dθ, частица должна пролететь вблизи одного из ядер по траектории, прицельный параметр которой заключен в пределах от b до b + db, причем dθ и db, как это следует из (А.5), связаны соотношением
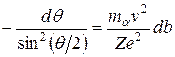 . (А.6)
. (А.6)
Знак «минус» в (А.6) обусловлен тем, что с увеличением b угол рассеяния убывает. Но так как далее нас будет интересовать лишь абсолютное значение db в функции от θ и dθ, знак минус учитывать не будем.
Обозначим площадь поперечного сечения пучка α-частиц буквой S. Тогда количество атомов рассеивающей фольги на пути пучка равно nSa, где n – число атомов в единице объема, a – толщина фольги. Если считать, что α-частицы распределены равномерно по сечению пучка и число их велико, то количество частиц dN, пролетающих вблизи одного из ядер по траектории с прицельным параметром от b до b+db, будет равно
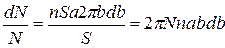 , (А.7)
, (А.7)
где N – общее количество частиц в пучке.
Выразив в (А.7) b и db через θ и dθ в соответствии с (А.5) и (А.6), получим
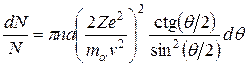 .
.
Далее преобразуем множитель, содержащий угол θ; тогда
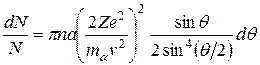 .
.
Выражение 2πsin θdθ есть телесный угол d Ω, в пределах которого заключены направления, соответствующие углам рассеяния от θ до θ + dθ. Учитывая, что кинетическая энергия α-частицы Tα = mαv 2/2, окончательно получаем
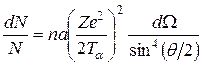 . (1.2)
. (1.2)
ПРИЛОЖЕНИЕ Б. Частица в прямоугольной потенциальной яме
Для простоты будем рассматривать прямоугольную потенциальную яму бесконечно большой глубины и конечной ширины a (рис. Б). Потенциальная энергия частицы (с массой μ) при x < 0 и x > a должна быть бесконечно велика, поэтому ее волновая функция за пределами ямы обращается в нуль. Внутри ямы, где U (x) = 0, уравнение Шредингера
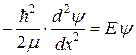 .
.
Введем следующее обозначение:
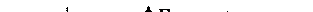
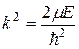 .
.
Тогда уравнение Шредингера будет выглядеть как
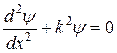 .
.
Его решением является функция
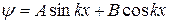 .
.
Это решение должно обращаться в нуль на границах потенциальной ямы. В результате В = 0 и
 .
.
Отсюда получим  , т.е.
, т.е.
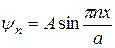
где n = 1, 2, 3 и т.д. Решение n = 0 следует отбросить как лишенное физического смысла. В этом случае волновая функция равна нулю тождественно, т.е. при всех значениях x. Но поскольку квадрат модуля волновой функции – это плотность вероятности обнаружить частицу в точке x, вероятность найти частицу где-либо в пространстве при n = 0 равна нулю (такой частицы просто нет).
Число n называется квантовым числом и равно целому числу длин полуволн де Бройля частицы
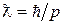
со средеквадратичным значением импульса 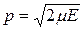 на отрезке длиной a (рис. Б). Энергия, соответствующая волновой функции с квантовым числом n, равна
на отрезке длиной a (рис. Б). Энергия, соответствующая волновой функции с квантовым числом n, равна
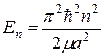 .
.
Остановимся подробнее на свойствах ψ -функций. Четность состояний, определяемая в данном случае как свойство ψ -функции менять или сохранять знак при замене координаты x на a – x, чередуется: функция ψ 1 нижнего по энергии (основного) состояния является четной, функция ψ 2 следующего (первого возбужденного) состояния – нечетной, и т.д. Волновые функции частицы четны или нечетны лишь в одномерной потенциальной яме, симметричной относительно середины. Функция ψ 1 не имеет узлов (т.е. не обращается в нуль) на всем интервале 0 < x < a. Функция ψ 2 имеет один узел, ψ 3 – два узла, и.т.д.
Число связанных состояний в потенциальной яме конечной глубины определяется ее глубиной (для бесконечной ямы оно бесконечно). В области, где En < U (x), волновые функции, хотя и быстро стремятся к нулю, но не обращаются в нуль тождественно (см. ПРИЛОЖЕНИЕ В): это происходит только при U → +∞.
Все это – общие, не зависящие от конкретного вида потенциала, свойства одномерного финитного движения – движения, совершающегося (по классическим представлениям) в ограниченной области пространства.
ПРИЛОЖЕНИЕ В. Квантовый гармонический осциллятор
Линейным, или одномерным гармоническим осциллятором называется частица, движущаяся в потенциале
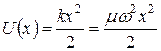
(величину k называют силовой постоянной). Согласно классической механике, такая частица совершает в направлении х гармонические колебания с циклической частотой 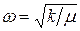 . Уравнение Шредингера для одномерного осциллятора
. Уравнение Шредингера для одномерного осциллятора
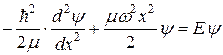 .
.
Если ввести безразмерные величины энергии и координаты
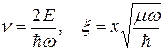 ,
,
то оно преобразуется в
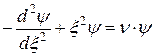 . (В.1)
. (В.1)
При ν = 1 решением этого уравнения является функция
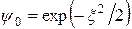 ,
,
в чем легко убедиться путем проверки. Это решение соответствует основному состоянию осциллятора, так как оно не имеет узлов. Энергия в основном состоянии равна  .
.
Решение, соответствующее n -му возбужденному состоянию должно иметь n (1, 2, 3 и т.д.) узлов. Такое число узлов имеет функция
 , (В.2)
, (В.2)
где 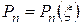 – полином n -й степени с некратными вещественными корнями.
– полином n -й степени с некратными вещественными корнями.
Используя то, что
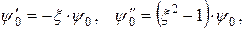
после подстановки (В.2) в уравнение (В.1) получим
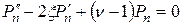 . (В.3)
. (В.3)
 Второе и третье слагаемые здесь являются полиномами степени n. Тогда, чтобы определить ν, достаточно сравнить коэффициенты при старших членах этих полиномов. Если коэффициент при ξ n в третьем слагаемом равен a (ν –1), то во втором слагаемом он будет равен –2 an. Так как соотношение (В.3) должно выполняться тождественно, при всех значениях ξ, то
Второе и третье слагаемые здесь являются полиномами степени n. Тогда, чтобы определить ν, достаточно сравнить коэффициенты при старших членах этих полиномов. Если коэффициент при ξ n в третьем слагаемом равен a (ν –1), то во втором слагаемом он будет равен –2 an. Так как соотношение (В.3) должно выполняться тождественно, при всех значениях ξ, то
 ,
,
что дает возможные значения энергии
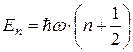 .
.
Таким образом, уровни энергии квантового линейного гармонического осциллятора эквидистантны, т.е. находятся на равных расстояниях друг от друга (рис. В).
ПРИЛОЖЕНИЕ Г. Биномиальное распределение, распределения Пуассона и Гаусса
Обозначим биномиальное распределение (5.8) как 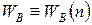 и вычислим для него среднее число ядер
и вычислим для него среднее число ядер 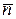 , распадающихся за некоторый промежуток времени. Для этого введем функцию
, распадающихся за некоторый промежуток времени. Для этого введем функцию
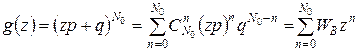
и найдем ее первую и вторую производные по параметру z в точке z = 1:
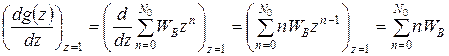 , (Г.1)
, (Г.1)
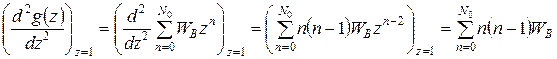 . (Г.2)
. (Г.2)
Согласно определению среднего,
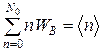 .
.
Тогда, в силу (Г.1)
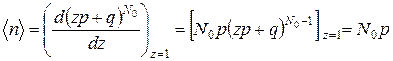 . (5.10)
. (5.10)
Чтобы найти дисперсию биномиального распределения, разложим выражение для квадрата отклонения случайной величины от среднего:
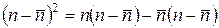 .
.
Можно видеть, что при усреднении второго слагаемого в этом выражении получается нуль, так как среднее отклонение от среднего равно нулю. Далее представим первое слагаемое в следующем виде:
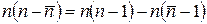 .
.
Используя определение дисперсии, найдем, что
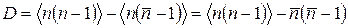 .
.
Далее воспользуемся тем, что, согласно (Г.2), среднее значение произведения n (n – 1) есть вторая производная функции g (z). Отсюда
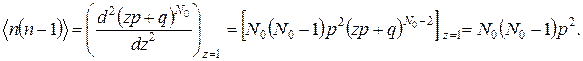
Тогда
 . (5.11)
. (5.11)
При 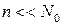 и р << 1 выражение (5.8) можно упростить. Подставляя, согласно (5.10),
и р << 1 выражение (5.8) можно упростить. Подставляя, согласно (5.10),  получаем:
получаем:
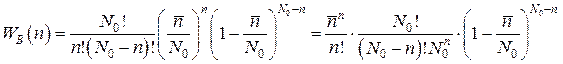 .
.
Осуществим предельный переход 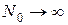 во втором множителе:
во втором множителе:
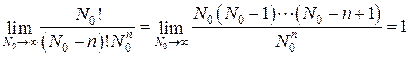 .
.
Аналогично, пользуясь определением второго замечательного предела
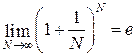 ,
,
получаем для третьего множителя
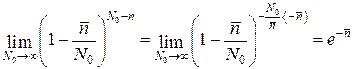 .
.
Таким образом,
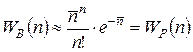 . (5.12)
. (5.12)
Полученное распределение WP (n) известно как распределение Пуассона.
Преобразуем соответствующим образом распределение Пуассона для 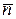 >>1. Во-первых, воспользуемся формулой Стирлинга для аппроксимации факториалов больших чисел
>>1. Во-первых, воспользуемся формулой Стирлинга для аппроксимации факториалов больших чисел 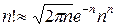 .
.
Тогда
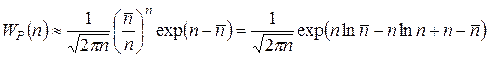 . (Г.3)
. (Г.3)
Во-вторых, используем тот факт, что распределение WР (n) заметно отлично от нуля лишь в довольно узкой области справа и слева от максимума (см. рис. 5.2). Тогда, раскладывая показатель экспоненты в (Г.3) в ряд Тейлора по 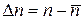 ,
,
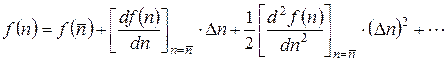 ,
,
с точностью до первого неисчезающего члена (в данном случае – второго порядка по Δ n) и заменяя под корнем 2 πn на 2 π 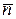 , получаем
, получаем
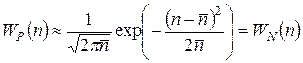 . (5.14)
. (5.14)
Выражение (5.14) представляет собой не что иное, как закон Гаусса, или нормальное распределение непрерывной случайной величины.[207]
ПРИЛОЖЕНИЕ Д. Преобразование Лапласа
Преобразованием Лапласа называется такая математическая операция, в результате которой функции -оригиналу N (t) ставится в соответствие функция F (p), называемая изображением функции N (t) и определяемая следующим образом:
 . (Д.1)
. (Д.1)
Из определения следует, что преобразование Лапласа обладает свойством линейности, т.е.
 .
.
Используя определение (Д.1) и применяя интегрирование по частям, можно показать, что изображение первой производной функции, дифференцируемой в точке t = 0, выглядит как
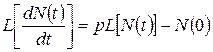 .
.
Обратная операция отыскания оригинала по его изображению
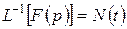
называется обратным преобразованием Лапласа. Обратное преобразование Лапласа также линейно.
Для отыскания оригиналов существуют таблицы, найти которые можно в математических справочниках. Приведем здесь краткую выдержку из подобной таблицы.
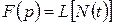
| 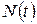
|
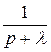
|
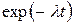
|
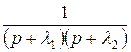
| 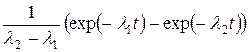
|
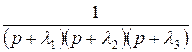
| 
|
Указанные свойства преобразования Лапласа и обратного ему преобразования позволяют использовать их для решения систем линейных дифференциальных уравнений с заданными начальными условиями. Рассмотрим решение двух первых уравнений системы, описывающей скорость радиоактивных превращений в простейшей цепочке из двух радионуклидов:
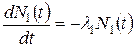 ,
,
 , (6.2)
, (6.2)
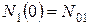 и
и 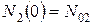 . Применим преобразование Лапласа к левой и правой частям этих уравнений. В результате, используя свойство линейности, получим следующую систему алгебраических уравнений
. Применим преобразование Лапласа к левой и правой частям этих уравнений. В результате, используя свойство линейности, получим следующую систему алгебраических уравнений
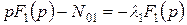 ,
,
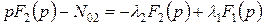 . (Д.2)
. (Д.2)
Выразим F 1(р) из первого уравнения системы (Д.2):
 .
.
Подставив этот результат во второе уравнение системы (Д.2), получим
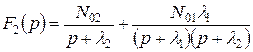 . (Д.3)
. (Д.3)
Пользуясь свойством линейности обратного преобразования, по таблице находим оригиналы N 1(t) и N 2(t):
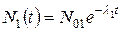 ,
,
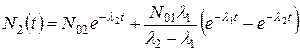 . (6.3)
. (6.3)
Если к первым двум уравнениям системы (6.2) добавить третье, соответствующее следующему превращению в радиоактивной цепочке,
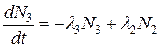 ,
,
 , то отыскание его решения полностью аналогично:
, то отыскание его решения полностью аналогично:
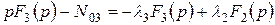 .
.
Подставляя в это уравнение F 2(р) из (Д.3), находим, что
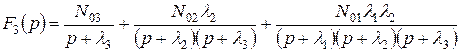 .
.
Отыскание оригинала по таблице приводит к следующему результату:
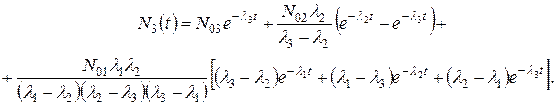
Решение более сложных систем (в том числе для разветвленных цепочек) методом преобразования Лапласа также не представляет трудности. Однако, как показывает последний пример, аналитические решения Ni (t) при больших i выглядят весьма громоздко. В этом случае для получения результата предпочтительнее использовать алгоритм Бейтмана, изложенный в п. 6.2.
ПРИЛОЖЕНИЕ Е. β-спектры
Для очень большого числа N β-распадов число распадов dN, при которых произойдет вылет электрона с импульсом от pe до pe + dpe и антинейтрино с импульсом pν, определяется как
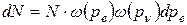 , (Е.1)
, (Е.1)
где ω (pe) и ω (pν) – вероятности того, что проекции импульсов p e и p ν примут значения pe и pν соответственно. Для каждой из двух частиц вероятность ω (p) пропорциональна площади сферы с радиусом р, т.е.
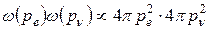 .
.
Перейдем от импульсов частиц к их энергиям. Кинетическая энергия электрона как релятивистской частицы
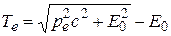
(E 0 = mec 2), откуда следует
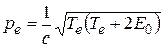 .
.
Дифференцируя Te по pe, получим
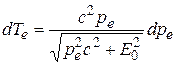 ,
,
 .
.
Вследствие малой массы нейтрино с любой энергией можно считать ультрарелятивистским, поэтому pν = E ν / c. Учтем закон сохранения энергии,[208] согласно которому  . Тогда
. Тогда
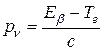 .
.
В результате подстановки pe, pν и dpe в (Е.1) найдем, что число распадов, при которых произойдет вылет электрона с энергией от Te до Te + dTe
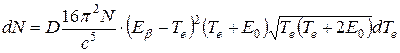 ,
,
где D – коэффициент пропорциональности. Таким образом, выражающая форму β-спектра функция 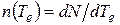 имеет вид
имеет вид
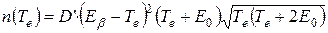 . (8.1)
. (8.1)
 При малых энергиях β-частиц форма спектра заметно искажается из-за кулоновского взаимодействия β-частиц с ядром, которое «включается» сразу же после распада. В случае β–-распада это взаимодействие является притягивающим и стремится уменьшить энергию вылетающего электрона. При β+-распаде кулоновское взаимодействие – отталкивающее и поэтому стремится ускорить вылетающий позитрон. В результате спектры электронов обогащаются, а спектры позитронов обедняются частицами с низкой энергией (рис. Е). Учет кулоновского взаимодействия приводит к следующей формуле для распределения β-частиц по энергиям:
При малых энергиях β-частиц форма спектра заметно искажается из-за кулоновского взаимодействия β-частиц с ядром, которое «включается» сразу же после распада. В случае β–-распада это взаимодействие является притягивающим и стремится уменьшить энергию вылетающего электрона. При β+-распаде кулоновское взаимодействие – отталкивающее и поэтому стремится ускорить вылетающий позитрон. В результате спектры электронов обогащаются, а спектры позитронов обедняются частицами с низкой энергией (рис. Е). Учет кулоновского взаимодействия приводит к следующей формуле для распределения β-частиц по энергиям:
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 512; Нарушение авторских прав?; Мы поможем в написании вашей работы!