Схемы соединения обмоток трансформаторов на тяговых подстанциях

Схемы одностороннего питания группы тяговых подстанций от линии передачи.

Схемы соединения обмоток трансформаторов на тяговых подстанциях.

Модуль 1. Системы электроснабжения электрифицированных дорог

Лекция №5, 6. Особенности схем питания однофазного тока промышленной частоты (2 часа)

План лекции:

3. Схемы двустороннего питания группы тяговых подстанций от линии передачи.

4. Особенности схем питания подстанций в реальных условиях.

На дорогах однофазного тока тяговая сеть, как правило, питается от трехфазной линии передачи через трансформаторы. Прежде чем переходить к рассмотрению питания тяговой сети через трансформаторы различных схем соединений, условимся о системе обозначений напряжений и токов в обмотках трансформаторов. При рассмотрении цепей переменного тока в электротехнике принято условливаться о направлениях электродвижущей силы (э.д.с.) и тока, которые принимаются за положительные.

Прежде всего, напомним, что у каждой обмотки условно назначает­ся «начало» и «конец». «Начало» обмоток согласно действующему стан­дарту обозначают начальными буквами алфавита (А, В, С), а «конец» — последними буквами алфавита (X, У, Z). При этом для обмоток высше­го напряжения используют прописные буквы А, В, С и X, У, Z, а для обмоток низшего напряжения — строчные а, б, с и х, у, z. Для одно­фазных трансформаторов обозначают соответственно A и X и а и х.

Если теперь принять, что направление намотки обмоток высшего и низшего напряжения одинаково и маркировка концов обмоток выс­шего и низшего напряжения выполнена, вдоль по сердечнику в одном порядке, то направления э.д.с. в обеих обмотках всегда будут совпа­дать (например, если в обмотке высшего напряжения от X к А, то и в обмотке низшего напряжения также от х к а).

Обычно в курсе электрических машин на векторной диаграмме трансформаторов э. д. с. первичной и вторичной обмоток показывают (принимают) совпадающими по фазе. При этом вектор напряжения во вторичной обмотке получается повернутым относительно вектора на­пряжения первичной обмотки на угол, близкий к 180°. Если пренебречь сопротивлением обмоток или «вынести» их во внешнюю цепь каждой стороны, то вектор первичного напряжения был бы равен и противо­положен вектору э.д.с. первичной обмотки, а вектор напряжения вто­ричной обмотки совпадал бы с э. д, с. вторичной обмотки, а так как э. д. с. обеих обмоток совпадают по фазе, то напряжение первичной об­мотки U₁было бы на 180° сдвинуто относительно напряжения вторич­ной обмотки U₂.

Принятое в рассматриваемых ниже схемах положение о совпаде­нии по фазе напряжений U₁ и U₂ (рис. 3.1) не противоречит вышеиз­ложенному. Все зависит от того, в каком контуре рассматривается та или иная величина. Направление, принятое за положительное в одном контуре, может оказаться отрицательным в другом и наоборот.

В теории машин как бы рассматривается контур, включающий в себя первичное и вторичное напряжение, при котором условные элект­рические связи заменяют действительные магнитные связи между це­пями первичной и вторичной стороны подобно тому, как это делается при переходе к схеме замещения трансформатора. При этом число вит­ков одной из обмоток приводится к напряжениям другой с соответст­вующим изменением э. д. с, токов и напряжений.

Если после этого вынести со­противления обмоток в соответ­ствующую цепь, то получим схему замещения, представленную на рис. 3.1.

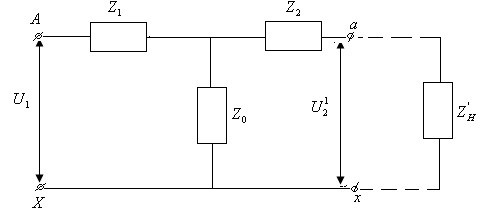
Рис. 3.1. К вопросу о расположения на векторной диаграмме

векторов первичного и вторичного напряжений

В самом четырехполюснике АХах напряжение U₁ уравновеши­вает напряжение U'₂ и падение на­пряжения в нем. Естественно, что здесь U'_z сдвинуто по отношению к U₁ на угол, близкий к 180°. По отношению же к потребителю (рис. 3.1, Z_н^’ - приведенная нагрузка) U₁ и U₂ совпадают по фазе (если пренебречь падением напряжения в обмотках транс­форматора) или близки к такому совпадению в действительности. Так как здесь и далее будут рассматриваться напряжения обмоток в контуре с потребителем, то векторы напряжений первичной и вто­ричной обмоток, расположенных на одном и том же стержне сер­дечника трансформатора, будут, естественно, приниматься совпадаю­щими по фазе. Следовательно, будет одинакова полярность зажимов А и а и соответственно X и х (рис. 3.2 а), будет совпадать по фазе и напряжение U_ах (между точками A и X) с напряжением U_ax (между точками а и х). Тогда взаимное расположение векторов э.д.c первич­ной и вторичной обмоток будет совпадать с взаимным расположением указанных векторов напряжений.

Если напряжения U_ax и U_ax совпадают по фазе, то (пренебрегая током холостого хода) можно сделать заключение, что совпадают по фазе и токи I_A и I_a, вызываемые ими в контурах соответственно пер­вичной и вторичной обмоток. Положительное направление этих токов I_A и I _а показано на рис. 3.2, а стрелками.

Как видно из рис. 3.2, а, ток в первичной обмотке, являющийся в своем контуре приемником энергии, направлен от начала обмотки А к концу X, а во вторичной обмотке, которая является в своем контуре ис­точником энергии, ток направлен от конца обмотки х к началу а.

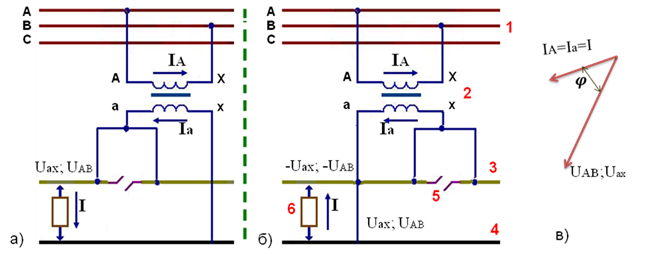
Рисунок 3.2. Схема питания тяговой сети однофазного тока с помощью однофазно­го трансформатора (а); то же при перемене концов вторичной обмотки (б) и векторная диаграмма (в):

1 — трехфазная линия передачи; 2 — однофазный трансформатор; 3 —контактная сеть; 4 — рельсы; 5 — секционирующее устройство; 6 — электровоз

Соот­ветственно векторная диаграмма (для трансформатора с коэффициентом трансформации, равным единице, и током холостого хода, равным ну­лю) получит вид, изображенный на рис. 3.2, в. За положительное на­правление тока в электрическом локомотиве будем принимать на­правление, совпадающее с положительным направлением тока во вто­ричной обмотке, т. е. от контактного провода к рельсу (см. рис. 3.2, а). На рис. 3.2, а и далее на последующих аналогичных рисунках над контактным проводом показано напряжение питающей трехфазной ли­нии, с которым по фазе совпадает напряжение в тяговой сети.

Наиболее простой является схема питания через однофазный транс­форматор (см. рис. 3.2, а). Здесь на всем протяжении линии справа и слева от подстанции тяговая сеть имеет напряжение U_ах, совпадающее по фазе с напряжением U_ab. Около подстанции сеть секционирована, что позволяет при повреждении отключать только половину линии, питаемой данной подстанцией. При однофазной подстанции одна фаза линии передачи остается ненагруженной. Само собой разумеется, что любая перемена концов обмоток трансформатора (первичной или вто­ричной на рис.3.2, (б) не изменит нагрузку линии передачи и может только привести к изменению по фазе (на 180°) напряжения в тяговой сети и соответственно тока локомотива. Направление тока принятое за положительное в локомотиве, теперь противоположно принятому на рис. 3.2, а.

Более равномерная нагрузка фаз трехфазной линии электропере­дачи достигается при питании тяговых подстанций поочередно от всех трех фаз этой линии. В этом случае секции тяговой сети слева и справа от подстанции в отличие от рассмотренной схемы питаются от различ­ных фаз линии передачи и, следовательно, имеют напряжения, не сов­падающие по фазе друг с другом. На дорогах СССР распространено пи­тание тяговой сети от трехфазных трансформаторов со схемой соедине­ния обмоток Y/∆. Применение трехфазных трансформаторов позволя­ет питать и трехфазные (нетяговые) потребители.

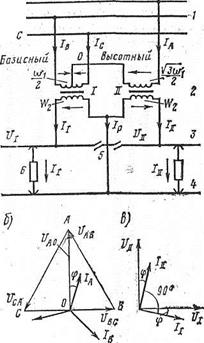
Вторичная обмотка трансформаторов соединяется в треугольник, например так, как это показано на рис. 3.3, а. Первичная обмотка соединена в звезду и, следовательно, напряжения в тяговой сети меж­ду контактным проводом и рельсами U_ас (слева на рис. 3.3, а) и между рельсами и контактным проводом U_cb (на рис. 3.3, а - справа) сов­падают по фазе с напряжениями первичной стороны соответственно U_А и U_С (см. рис.3.3, б). Схема на рис. 3.3 является трехфазно-двухфазной. В общем случае при этой схеме трехфазная система нагру­жается неравномерно.

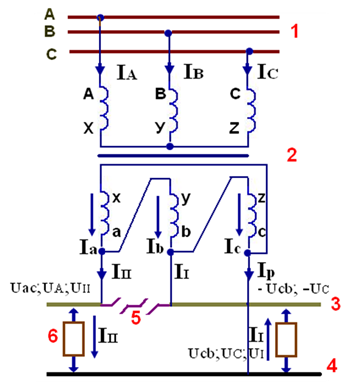
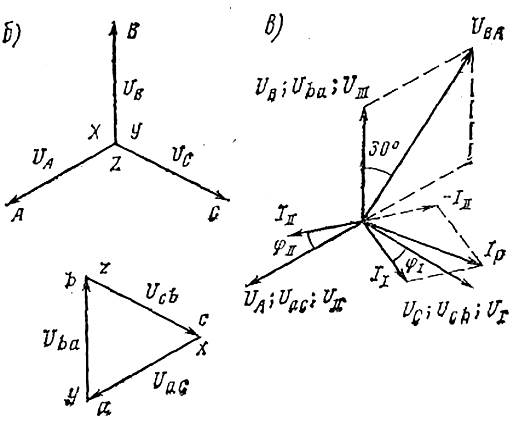
Рис. 3.3. Схема питания тяговой сети однофазного тока с помощью трехфазного трансформатора, соединенного по схеме Y/A—11 (а); векторная диаграмма на­пряжений первичной и вторичной обмоток (б), векторная диаграмма напряже­ний и токов (в):

1 - трехфазная линия передачи; 2 - трехфазный трансформатор;

3 - контактная сеть; 4 - рельсы; 5 - нейтральная вставка; 6 - электровоз

Зажимы трансформаторов А, В и С не всегда присоединяются к од­ноименным фазам линии передачи. Поэтому напряжения на примыкающих к подстанции фидерных зонах не всегда будут совпадать с показан­ными на рис. 3.3, а следовательно, и обозначения токов в фидерах, пи­тающих контактную сеть, не следует связывать с обозначениями фаз трехфазной системы.

Обратим внимание на то, что напряжение в фидерных зонах совпа­дает по фазе с фазными напряжениями двух фаз трехфазной системы, в данном случае U_c (справа на рис. 3.3) и U_a (слева). Эти фазы услов­но назовем рабочими, а третью фазу В - нерабочей. Эту нерабочую фа­зу В обозначим цифрой III и тогда соответственно ходу вращения век­торов фазу С- цифрой I и фазу А цифрой II.

Обратим внимание на то, что напряжение фазы I будет опережать напряжение фазы II на 120°. В связи с этим фаза I (рабочая) часто име­нуется опережающей (относительно рабочей II), а фазе II (тоже рабо­чая) - отстающей (от другой рабочей I). Соответственно на рис. 3.3 ток левого фидера обозначен через I_II, правого через I_I, а присоеди­ненного к рельсам — через I_р.

При рассмотрении различных многофазных схем тяговых подстан­ций с целью унификации изложения и в соответствии с принятым вы­ше за положительное направление токов (I_А, Iв, Iс) в линии передачи, в ответвлениях от линии передачи к подстанции, в первичной обмотке трансформатора будем принимать направление от питающего центра к потребителю. За положительное направление токов в электрических локомотивах примем направление, совпадающее е положительным на­правлением, напряжения фазы. Для схемы питания рис.3.3, а векторная диаграмма напряжений первичной и вторичной обмоток показана на рис; 3.3, б, а совмещенная векторная диаграмма напря­жений и токов - на рис.3.3, в. Если принять коэффициент транс­формации равным единице, пренебречь током холостого хода и потеря­ми напряжения в обмотках, то (в соответствии, с принятыми выше усло­виями) напряжения на первичных обмотках Uа = Uах; Ub = Uby; Uc = Ucz и на вторичных U_сЬ = U_cz будут равны и совпа­дать по фазе. Тогда напряжения U_A, Ub и Uc и соответственно на­пряжения U_ac, U_ba и U _сЬбудут представлены одними и теми же векторами (рис. 3.3, в). Вектор тока I_II (слева) принятого направления следует ориентировать относительно вектора напряжения U_ii = U_ac. На векторной диаграмма показан ток I_II сдвинутый от «своего» напряжения на некоторый угол φ_II.

Вектор тока I_I (идущего вправо от подстанции) откладывается со сдвигом на некоторый угол φ_I от вектора «своего» напряжения Ui = U_cb (см. рис. 3.3, б). Ток в проводе, присоединенном к рельсу I _р, равен разности токов I_I и I_II.

Установим правило, по которому токи фидеров I_I и I_II распреде­ляются между вторичными обмотками трансформатора.

В теории электрических машин доказывается, что для схемы Y/∆ (или Y/Y/∆), т.е. для схемы, где отсутствуют токи нулевой последова­тельности, каждую фазу трансформатора и при несимметричной нагруз­ке можно рассматривать независимо от другой, т. е. как однофазный трансформатор. При этом в замкнутом контуре треуголь­ника не может возникнуть однофазный ток нулевой последователь­ности, и распределение нагрузок на вторичной стороне между фазами трансформатора определяется только соотношением сопротивлений обмоток. Напряжение левой фидерной зоны (с током I_II) U_II=U_ac. Это напряжение генерируется как бы в двух параллельно соединенных источниках электрической энергии вторичной цепи (рис.5.3, а); первым является обмотка ах, а вторым - последовательно соединен­ные обмотки by и cz (где оно получается в результате геометрического сложения напряжений двух обмоток by и cz). Но сопротивление обмотки ах в 2 раза меньше сопротивления двух других об­моток, соединенных последова­тельно. Поэтому ток I_II разде­ляется между этими генерирую­щими напряжение U _ас обмотка­ми в отношении 2:1. Аналогич­ным образом делится и ток I_II.

Эти соображения позволяют построить векторную диаграмму токов в обмотках трансформато­ра (рис.3.4).

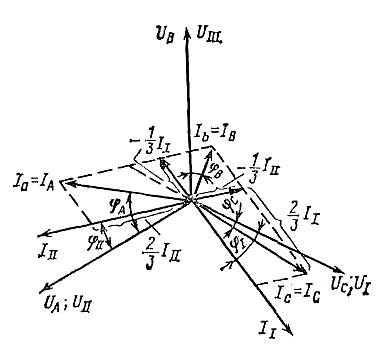
Надо обратить внимание на знаки токов в об­мотках, вызываемых токами II и III (см. рис. 3.3, а). В контуре, состоящем из обмотки ха и нагрузки левой зоны I_II, положительные направления токов 1_а и I_II совпадают и, следовательно, в состав I_а входит ⅔ I_II со знаком плюс. В контуре же, состоящем из обмоток cz и by итой же нагрузки левой зоны I_II направления токов, принятые за положительные, противо­положны и поэтому в токи I_b и I_с входит 1/3 I_II со знаком минус.

Ток I_I точно так же определяется напряжением U_I, равным U_cb. Оно создается в обмотках сz и в соединенных последовательно by и ах. Точки cub (см. рисунок 1.12, а) являются точками параллельного «соединения двух источников энергии с напряжением U_I = U_cb. В состав I_с входит часть I_I, равная ⅔ I_I. Часть I_I, равная ⅓ I_I, входит в состав токов I_a и I_b со знаком минус (см. рисунок 1.13). Ток в обмотке ах I_a, исходя из изложенного, должен равняться разности ⅔ İ_II и ⅓ İ_I. Ток в фазе А звезды первичной обмотки при принятых выше условиях равен току I_а, т.е. I_A = 1_а.

Аналогично ток в обмотке сz равен разности токов ⅔İ_I и ⅓İ_{I I} (см. рисунок 1.13), соответственно I_C = I_с.

Из рассмотренных контуров (см. рисунок 1.12, а) видно, что нагрузка в обмотке by составляется из суммы (-⅓ I_I) и (-⅓ I_II) Сложив эти векторы (см. рисунок 1.13), получим нагрузку третьей, наименее нагруженной фазы I_b = I_B. Можно заметить (см. рисунок 1.13 и рисунок 1.12, а), что наименее нагруженной фазой является та фаза треугольника, которая непосредственно не соединена с рельсами. На векторной диаграмме рисунок 1.12, б это фаза В. В частном случае, когда одна из нагрузок I_II или I_I равна нулю, наименее нагруженными оказываются две фазы.

Значения токов, показанные на векторной диаграмме рисунок 1.13, можно получить и непосредственно из уравнений Кирхгофа. Если в рассматриваемый момент времени справа от подстанции нагрузка I_I и слева I_II (см. рисунок 1.12, а), то можно написать:

– İ_I = İ_b – İ_c; İ_II = İ_a – İ_b; İ_p = İ_c – İ_a, (3.1)

Кроме того, известно, что

İ_a + İ_b + İ_c=0, (3.2)

Решив эти уравнения относительно İ_a, İ_b, и İ_c получим

İ_c = 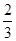İ_I – 1 İ_II; İ_a = 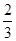İ_II – 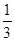İ_I; İ_b = – 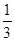İ_I – 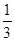İ_II (3.3)

Полученные уравнения (3.3) соответствуют векторной диаграмме рисунка 1.13, где показаны углы сдвига фаз φ_А, φ_В, φ_С между напряжени­ями U_А, U_В, U_С и токами I_A, I_B и I_C соответственно. Заметим, что φ_А ˃ φ_II, а φ_C < φ_I, т. е. углы сдвига φ_А и φ_С для двух наиболее загруженных фаз оказываются разными даже при φ_II = φ_I. Причем у первой (обозначенной I) «опережающей» (по ходу вращения векторов) фазы (в данном случае фазы С) угол меньше, чем у «отстающей» фазы А (обозначенной II). Если посмотреть на формулы (3.3) для I_c и I_a, то по написанию они сходны, как и их первые члены. Что касается вторых членов, то из диаграммы рисунка 1.13 видно, что ток (–⅓ I_I), входящий в величину I_a, отстает по, фазе от напряжения U_{I I} (U_A), а ток (–⅓ I_II), входящий в величину I_c, опережает по фазе напряжение U_I (U_C) Это обстоятельство, как увидим в дальнейшем, существенно влияет на потери напряжения в трансформаторе и питающей линии. В данном случае нерабочей (т. е. наименее загруженной) фазой оказалась фаза В, а рабочими А и С. В дальнейшем для получения более равномерной нагрузки питающей трехфазной системы нерабочие фазы на подстанциях будут чередоваться, а следовательно, будут чередоваться и сочетания рабочих фаз. Другими словами, если нерабочими фазами на подстанциях поочередно будут В, С, А, В, то соответственно рабочими будут А и. С, А и В, В и С, А и С и т. д. И в каждом случае одна из них будет опережающей фазой (I), а другая отстающей (II), и поэтому у одной из них угол сдвига фаз между током и напряжением будет меньше соответствующего угла у нагрузки, а у другой, наоборот, – больше. Так как в дальнейшем придется различать между собой эти фазы, введем дополнительное обозначение фаз I, II и III независимо от того, с напряжением какой фазы трехфазной системы фактически совпадает их напряжение. Таким образом, на каждой подстанции нумеруем фазы так, чтобы нерабочая всегда имела номер III.

Как известно, соединяя различным образом первичные или вторичные обмотки, можно создать ряд групп соединений этих обмоток. В частности, разные группы можно получить и для схемы Y/∆,пересоединяя выводы вторичной обмотки. Согласно стандарту различные группы соединения обмоток характеризуются взаимным расположением векторов э.д.с. первичных и вторичных обмоток, действующих между одноименными зажимами. При этом для оценки сдвига фаз вектор э.д.с. обмотки высшего напряжения мысленно совмещают с минутной стрелкой часов, установленной на цифре 12, тогда часовая стрелка, занимая различное положение на циферблате, показывает цифру, которой обозначается данная группа соединения.

Выше было принято, что направление намотки и маркировка обмоток выполнены таким образом, что взаимное расположение векторов э. д. с. первичной и вторичной обмоток будет совпадать с взаимным расположением соответствующих векторов напряжений. Следовательно, оценку групп соединений трансформаторов можно производить не по э. д. с, а по этим векторам напряжений. Это позволит не изображать э. д. с. обмоток и упростит построение векторных диаграмм и все дальнейшее изложение.

На разобранной выше схеме (см. рисунок 1.12, а)треугольник на вторичной обмотке образован соединением начала первой фазы а с концом второй у, начала второй в с концом третьей z и начала третьей с с концом первой х. При этом вектор линейного напряжения первичной стороны U_BA отстает от вектора линейного напряжения вторичной стороны U_ba на 30° (см. рисунок 1.12, в). Если вектор U_ВА совместить с минутной стрелкой часов, установленной на цифре 12. то вектор вторичного напряжения совпадает с часовой стрелкой, показывающей 11. Такая группа соединения, как известно, получила обозначение Y/∆ – 11.

Треугольник мог бы быть получен соединением конца первой фазы х с началом второй b, конца второй у с началом третьей с и т. д. (рисунок 1.14, а). При этом можно так присоединить трансформатор к тяговой сети, что наименее нагруженной останется опять фаза В (та фаза, которая в треугольнике непосредственно не соединяется рельсами).

В рассматриваемой схеме вектор линейного напряжения первичной стороны U_BC (рисунок 1.14, б) опережает по фазе вектор линейного напряжения вторичной стороны U_bс на 30°. Такая схема обозначается Y/∆ –1. Если присоединить трансформатор к тяговой сети так, чтобы слева и справа сохранились напряжения соответственно U_А и U_С,то токи нагрузки по сравнению с рисунка 1.12 изменятся на противоположные (как в случае однофазного трансформатора при перемене концов одной из обмоток). Составив уравнения, аналогичные уравнениям (1.1) - (1.3), можно легко убедиться, что нагрузка фаз на первичной стороне не изменяется по сравнению с нагрузками рисунка 1.13.

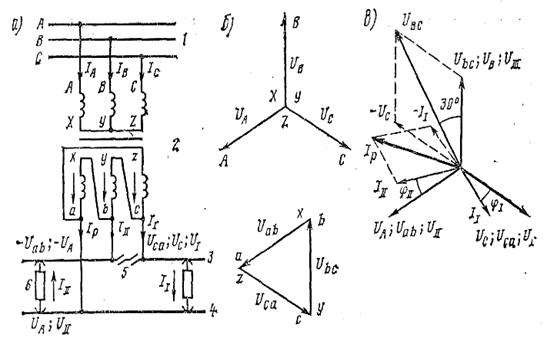
Рисунок 3.4. Схема питания тяговой сети однофазного тока с помощью трехфазного трансформатора, соединенного по схеме Y/∆ –1

Наиболее простой из многофазных является схема соединения обмоток трансформаторов в открытый (или неполный) треугольник. Схемой открытого треугольника называется схема, в которой (как и выше в полном треугольнике) конец обмотки одной фазы соединяется с началом обмотки другой, но в которой отсутствует одна из фаз. Такая схема может осуществляться как с помощью двух однофазных трансформаторов (рисунок 3.5 и 3.6), так и с помощью одного трехстержневого трансформатора с двумя обмотками.

Положительное направление токов показано в линии передачи от питающего центра к потребителю (I_A, I_B, I_C),в фидерах тяговой сети от подстанции к сети и на локомотивах в соответствии с напряжением. На рисунке 3.5, а слева от подстанции напряжение Uа₁х₁ = U_АВ = U_I,а напряжение справа между рельсами и контактным проводом Uа₂х₂ = U_ВС =. U_II,напряжение между контактным проводом и. рельсов (– Uа₂х₂) = (– U_BC). Векторная диаграмма для схемы рисунка 3.5, а представлена на рисунке 3.5, б. Для простоты, как и выше, принято, что коэффициент трансформации равен единице, ток холостого хода и падение напряжения в обмотках трансформаторов равны нулю. Вектор тока I_I ориентируем относительно вектора U_AB = U_II и вектор I_II относительно, вектора U_BC=U_II. Из векторной диаграммы рисунка 3.5, б видно, что наиболее загруженной фазой линии передачи оказывается фаза В. В схеме рисунка 3.5, а открытый треугольник образован соединением точек Х ₁с А ₂ и соответственно х ₁ с а ₂. Если сохранить схему присоединения первого трансформатора к линии передачи и соединить начало первой обмотки А ₁с концом второй Х ₂ и соответственно а₁ с х ₂,присоединив к рельсу при этом точку а₁ х ₂вместо точки х ₁ а ₂ (рисунок 3.6, а), то векторная диаграмма будет иметь тот же характер, только наиболее загруженной окажется теперь фаза А линии передачи (рисунок 3.6, б).

Если на первичной и вторичной стороне соединить не начало одной фазы с концом другой, а, например, их концы, то получится так называемая неполная звезда (без одного луча) (рисунок 3.7). Однако, как нетрудно понять из схемы (рисунок 3.7, а) и векторной диаграммы (рисунок 3.7, б), нагрузка трехфазной линии передачи от этого не изменится (по сравнению с нагрузкой рисунок 3.5).

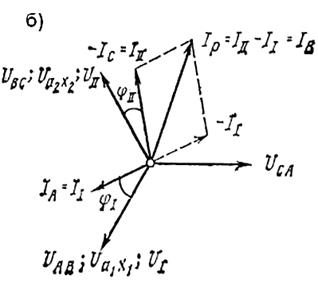
Рисунок 3.5. Первый вариант схемы питания (а) и векторная диаграмма (б)тяговой сети однофазного тока с помощью двух однофазных трансформаторов 2, соединенных в открытый треугольник (остальные обозначения те же, что на рисунке 1.11)

Рисунок 3.6. Второй вариант схемы питания (а) и векторная диаграмма (б)тяговой сети однофазного тока с помощью двух однофазных трансформаторов, соединенных в открытый треугольник

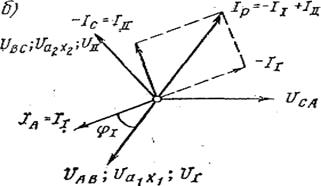
Рисунок 3.7. Схема питания тяговой сети однофазного тока с помощью двух однофазных трансформаторов соединенных в неполную звезду

а) я ¹ в

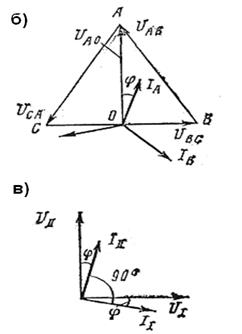
Рисунок 3.8. Схема питания тяговой сети с помощью трехфазно-двухфазного трансформатора (схема Скотта):

а – схема питания; б – векторная диаграмма трансформатора; в – векторная диаграмма для фидерных зон. 2 – трехфазно-двухфазный трансформатор Скотта

В приведенных на рисунках 1.12-1.17 схемах напряжения тяговой сети в смежных фидерных зонах, примыкающих слева и справа к данной подстанции (если считать за напряжение в контактной сети разность потенциалов контактного провода и рельсов), сдвинуты на угол π/3 и даже при равных нагрузках I_I = I_II и равных углах сдвига фаз φ _II =φ _I не обеспечивают равномерной нагрузки фаз трехфазной линии передачи.

В п. 4.4 в общем виде показано, что если две смежные зоны питать от двухфазной системы, т. е. при сдвиге напряжений в тяговой сети смежных фидерных зон на угол π/2, то при равных нагрузках I_I = I_II можно получить равномерную нагрузку трехфазной системы. Для этой цели могут быть использованы различные специальные трансформаторы. Наиболее распространенным является трехфазно-двухфазный трансформатор Скотта. Этот трансформатор состоит из двух однофазных трансформаторов с различными коэффициентами трансформации, включенных по специальной схеме (рисунок 3.8, а). Оба вывода трансформатора I, называемого «базисным», и один из выводов трансформатора II называемого «высотным», присоединяют к проводам линии передачи. Конец 0 первичной обмотки трансформатора II соединяется со средней точкой обмотки трансформатора I. Из топографической диаграммы (рисунок 1.18, б) видно, что напряжение U_AO на первичной обмотке трансформатора II равно √3/2 U_BC (U_BC – линейное напряжение трансформатора I). Так как напряжения в тяговой сети на фидерных зонах слева и справа от подстанции должны быть одинаковыми, коэффициенты трансформации трансформаторов I и II получаются различными. Вторичные обмотки имеют одинаковое число витков. При холостом ходе напряжения на вторичной стороне трансформаторов равны и сдвинуты на угол π/2.

Рассмотрим случай, когда нагрузки слева I_I и справа I_II; равны и сдвинуты на угол π/2, т. е. İ_I = – jİ_II и φ _I = φ _II. Найдем для этого случая токи I_A, I_B и I_C. По закону Кирхгофа для точки 0 (см. рисунок 3.8, а) можно записать:

İ_A,+ İ_B + İ_C =0. (3.4)

Из условия равновесия магнитодвижущих сил (пренебрегая током холостого хода) сумма их в каждом трансформаторе равна нулю:

İ_A 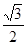ω₁ – İ_IIω₂ =0, (3.5)

İ_B 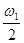– İ_C 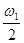– İ_Iω₂ =0, (3.6)

Преобразуем уравнения (3.4) - (3.6), учитывая, что İ_I = – j İ_II получим:

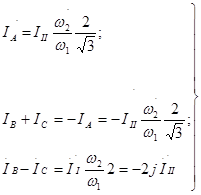(3.7)

или

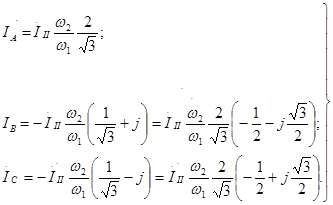(3.8)

Модули всех полученных токов равны между собой и токи повернуты друг относительно друга на угол 2π/3, т.е. трехфазная система нагружена равномерно. Векторная диаграмма, соответствующая уравнениям (3.8), представлена на рисунке 3.9, а взаимное расположение векторов токов и напряжений – на рисунке 3.8, б.

Дата добавления: 2015-05-26