
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нескінченно малі і нескінченно великі функції
|
|
|
|
Основні теореми про границі
Практичне обчислення границь ґрунтується на наступних теоремах.
Якщо існують 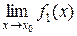 і
і 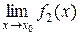 , то:
, то:
1) Границя суми (різниці) двох функцій дорівнює сумі (різниці) їхніх границь:
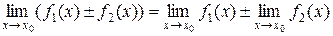 .
.
2) Границя добутку двох функцій дорівнює добутку їхніх границь:
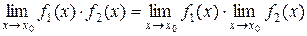 .
.
3) Границя частки дорівнює границі чисельника, поділеній на границю знаменника, за умови, що границя знаменника не дорівнює нулю:
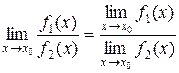 , якщо
, якщо 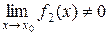 .
.
4) Постійний множник можна виносити за знак границі:
 , якщо
, якщо 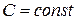 .
.
5) Границя степеня з натуральним показником дорівнює такому же степеню границі:
 .
.
Використовуються також наступні визначні границі:
І) 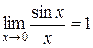 (перша визначна границя).
(перша визначна границя).
Наслідки із першої визначної границі:
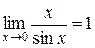 ;
;  ;
; 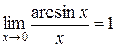 ;
; 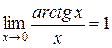 ,
,
а також:
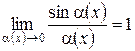 ;
; 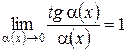 ;
; 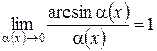 ;
; 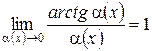 ,
,
де 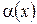 – деяка функція.
– деяка функція.
ІІ) 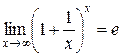 (друга визначна границя) або
(друга визначна границя) або 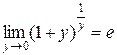 .
.
Наслідки із другої визначної границі:
 ;
; 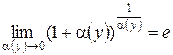 ,
,
де 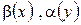 – деякі функції.
– деякі функції.
Функція 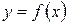 називається нескінченно малою при
називається нескінченно малою при  , якщо
, якщо
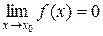 .
.
За визначенням границі функції рівність 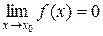 означає, що для заданого завгодно малого числа
означає, що для заданого завгодно малого числа  знайдеться таке число
знайдеться таке число  , що для всіх
, що для всіх 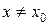 , що задовольняють нерівності
, що задовольняють нерівності  , буде виконуватися нерівність
, буде виконуватися нерівність  .
.
Функція 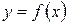 називається нескінченно великою при
називається нескінченно великою при  , якщо
, якщо
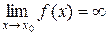 .
.
За визначенням границі функції рівність 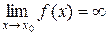 означає, що для заданого завгодно великого числа
означає, що для заданого завгодно великого числа  знайдеться таке число
знайдеться таке число  , що для всіх
, що для всіх 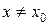 , що задовольняють нерівності
, що задовольняють нерівності  , буде виконуватися нерівність
, буде виконуватися нерівність 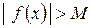 .
.
Зауваження: Аналогічно, можна говорити про нескінченно великі і нескінченно малі функції при 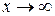 .
.
Нескінченно великі і нескінченно малі функції мають наступні властивості.
Властивість 1.Сума скінченної кількості нескінченно малих функцій є функцією нескінченно малою.
Властивість 2. Добуток обмеженої функції на нескінченно малу функцію є функцією нескінченно малою.
Властивість 3. Добуток постійної на нескінченно малу функцію є функцією нескінченно малою.
Властивість 4. Добуток скінченної кількості нескінченно малих функцій є функцією нескінченно малою.
Властивість 5. Сума скінченної кількості нескінченно великих функцій є функцією нескінченно великою.
Властивість 6. Добуток обмеженої функції на нескінченно велику функцію є функцією нескінченно великою.
Властивість 7. Добуток постійної на нескінченно велику функцію є функцією нескінченно великою.
Властивість 8. Функція, обернена за величиною нескінченно великий, є функцією нескінченно малою
Властивість 9. Функція, обернена за величиною нескінченно малій, є функцією нескінченно великою.
Зауваження: властивості 8 й 9 відображають зв'язок між нескінченно великою і нескінченно малою функціями.
Якщо прийняти наступні позначення: нескінченно мала функція – символ 0, нескінченно велика функція – символ ¥, постійна величина – символ 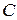 , обмежена функція – символ
, обмежена функція – символ 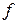 , то всі викладені властивості можна записати в такий спосіб:
, то всі викладені властивості можна записати в такий спосіб:
1. 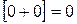 ; 4.
; 4. 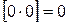 ; 7.
; 7.  ;
;
2. 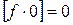 ; 5.
; 5. 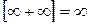 ; 8.
; 8. 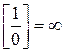 ;
;
3. 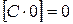 ; 6.
; 6. 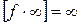 ; 9.
; 9. 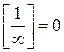
Для порівняння двох нескінченно малих функцій 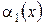 і
і  при
при  знаходять границю їх відношення:
знаходять границю їх відношення:

1) Якщо  , то
, то 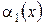 називається нескінченно малою функцією більш високого порядку в порівнянні із
називається нескінченно малою функцією більш високого порядку в порівнянні із 
2) Якщо 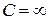 то
то  називається нескінченно малою функцією більш високого порядку в порівнянні із
називається нескінченно малою функцією більш високого порядку в порівнянні із 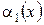
3) Якщо  , то
, то 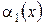 й
й  називаються нескінченно малими функціями одного і того ж порядку.
називаються нескінченно малими функціями одного і того ж порядку.
4) Якщо 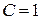 , те
, те 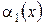 й
й  називаються еквівалентними (рівносильними) нескінченно малими:
називаються еквівалентними (рівносильними) нескінченно малими: 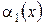 ~
~  .
.
При обчисленні границь використовують наступні заміни еквівалентних нескінченно малих функцій при 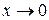 або
або 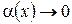 :
:
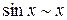 ,
, 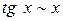 ,
, 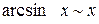 ,
,  ,
,
 ,
, 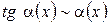 ,
,  ,
, 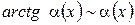 ,
,
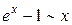 ,
, 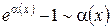 ,
, 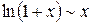 ,
, 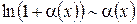 .
.
Варто зауважити, що границя відношення нескінченно малих функцій дорівнює границі відношення еквівалентних їм нескінченно малих функцій.
Зауваження: заміну нескінченно малих функцій на еквівалентні їм нескінченно малі функції не можна робити у випадку різниці нескінченно малих функцій.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 4419; Нарушение авторских прав?; Мы поможем в написании вашей работы!