Неперервність функції

Приклад 8.

Приклад 7.

Обчислити границю .

Розв’язок.

Підставимо замість 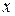граничне значення:

.

Для розкриття даної невизначеності перетворимо вираз у дужках – виділимо цілу частину.

.

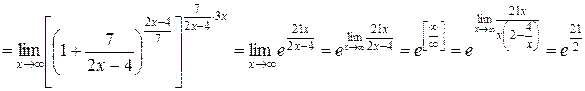Невизначеності , і 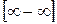зводять до виду 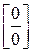або 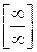за допомогою перетворення функції до дробу.

Обчислити границі: а) ; б) .

Розв’язок.

а)

.

б)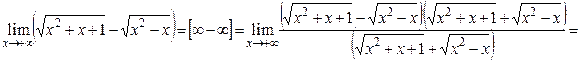

.

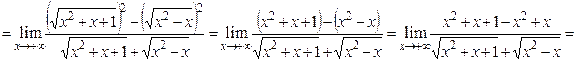
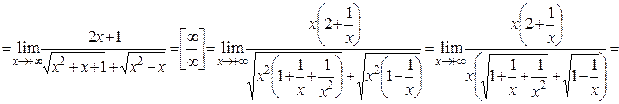
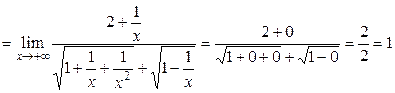Функція 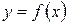називається неперервною в точці 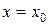, якщо виконані наступні три умови:

1) функція 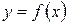визначена в точці 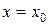і у її околі,

2) існує скінченна границя ,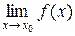

3) ця границя дорівнює значенню функції в точці 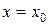, тобто .

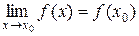Функція 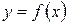називається неперервною на інтервалі , якщо вона неперервна в кожній точці цього інтервалу.

Точка 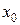, у якій не виконана хоча б одна із трьох умов неперервності, називається точкою розриву функції. Так, наприклад, всі точки, що не належать області визначення функції є точками розриву.

Всі точки розриву функції розділяють на точки розриву першого і другого роду.

Точка розриву 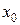називається точкою розриву першого роду функції 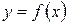, якщо в цій точці існують скінченні границі функції зліва та справа (односторонні границі), тобто 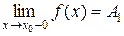і 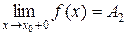, і при цьому:

1) якщо 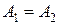, то точка 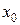називається точкою усувного розриву;

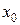2) якщо , то точка називається точкою скінченного розриву.

Величину 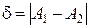називають стрибком функції в точці розриву першого роду.

Точка розриву 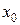називається точкою розриву другого роду функції 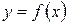, якщо в цій точці хоча б одна з її односторонніх границь (зліва або справа) не існує або є нескінченною.

Дата добавления: 2015-05-26