Умовний екстремум 1 страница

.

. Два единственно возможных события, обра­зующих полную группу, называются противоположными.

Если событие обозначено через А, то противоположное ему событие обозначается через 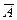. Из теоремы 17.2 следует, что

Например, если при стрельбе по мишени попадание — это событие А, то событие 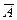— это промах; сумма их вероятностей равна единице — при выстреле обязательно будет либо попа­дание, либо промах. То же самое и при подбрасывании монеты: обязательно выпадет либо орел, либо решка.

Пример 3. В магазине имеется 10 телевизоров, из которых 2 неисправных. Найти вероятность того, что среди наугад взя­тых 3-х телевизоров будет хотя бы один неисправный.

Решение. События "среди взятых телевизоров нет ни од­ного неисправного" и "есть хотя бы один неисправный" — про­тивоположные. Первое из них обозначим через А, а второе — через 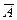. Общее число способов, которыми можно взять 3 изде­лия из десяти, равно C . Число исправных телевизоров равно 8, число способов выборки из них трех изделий равно C 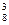, так что вероятность Р(А) = C 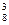/С . Искомая вероятность опреде­ляется из формулы (17.4):

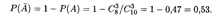
93. Сумма и произведение случайных событий. Теорема сложения вероятностей: для двух произвольных событий, для двух несовместных событий, для нескольких попарно несовместных событий.

Вероятность появления какого-либо из двух несовместных событий равна сумме вероятностей этих со­бытий:

Следствие. Вероятность появления какого-либо из нескольких попарно несовместных событий равна сумме их вероятностей:

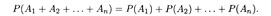
Пример 1. Стрелок стреляет по мишени, разделенной на 4 концентрические зоны. Вероятности попадания в эти области соответственно равны 0,4, 0,3, 0,2 и 0,1. Найти вероятность попадания либо в первую, либо во вторую зоны.

Решение. Пусть событие А — попадание в первую зону мишени, а событие В — попадание во вторую зону мишени. Эти события несовместны, поэтому применимы теорема 17.1 и формула (17.3) сложения вероятностей. Искомая вероятность равна

Сумма вероятностей событий, образующих полную группу, равна единице:

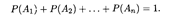
Произведением двух событий А и В называ­ется событие АВ, означающее совместное появление этих со­бытий (см. гл. 1.1, произведение множеств).

Например, если событие А — шар, событие В — белый цвет, то их произведение АВ — белый шар. Аналогично опре­деляется произведение нескольких событий, как совместное по­явление их всех.

Если при вычислении вероятности события никаких дру­гих ограничений кроме необходимого комплекса условий S не налагается, то такая вероятность называется безусловной. Ес­ли же налагаются другие дополнительные условия, содержа­щие случайные события, то вероятность такого события назы­вается условной.

Определение 2. Вероятность события В в предположении о наличии события А называют условной вероятностью Р_A(В).

Пример 1. В ящике лежит 11 деталей, 3 из них нестандарт­ные. Из ящика дважды берут по одной детали, не возвращая их обратно. Найти вероятность того, что во второй раз из ящика будет извлечена стандартная деталь — событие В, если в пер­вый раз была извлечена нестандартная деталь — событие А.

Решение. После первого извлечения в ящике из 10 дета­лей осталось 8 стандартных, и, следовательно, искомая веро­ятность

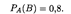
Пусть теперь известны вероятность Р(А) события А и условная вероятность Р_А(В) события В. Тогда справедлива следующая теорема.

ТЕОРЕМА 3. Вероятность произведения двух событий определяется формулой

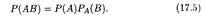
Пример 2. В условиях примера 1 найти вероятности того, что в первый раз извлечена нестандартная деталь, а во второй раз — стандартная, и наоборот.

Решение. Итак, событие А — это извлечение из ящика не­стандартной детали, а событие В — стандартной. Тогда воз­можны два случая. 1) Вероятность Р(А) = 3/11, а условная вероятность Р_A(В) = 0,8. Искомая вероятность произведения этих событий (их совместного появления в указанном порядке) равна, согласно теореме 17.3,

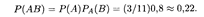
94. Теорема умножения вероятностей: для двух произвольных событий; для двух независимых событий; для нескольких событий, независимых в совокупности.

Событие В называется независимым от со­бытия А, если условная вероятность события В равна его без­условной вероятности (появление события А не влияет на ве­роятность события В):

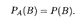
Отсюда следует, что и событие А также независимо от со­бытия В:

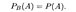
Для независимых событий теорема умножения вероятностей 17.3 в общей форме, которая следует из (17.6), имеет вид

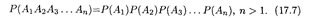
Равенство (17.7) принимается за определение независимых со­бытий. При этом если события независимы, то независимы также и соответствующие им противоположные события.

Пример 4. Найти вероятность поражения цели при совмест­ной стрельбе тремя орудиями, если вероятности поражения цели орудиями соответственно равны 0,9, 0,8 и 0,7 (события А, B и С).

Решение. Поскольку события А, В и С являются независимыми, то искомая вероятность вычисляется, согласно формуле (17.7), при n = 3:

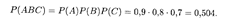
Когда в результате испытания может иметь место n неза­висимых событий с известными вероятностями их появления, особый интерес представляет случай нахождения вероятнос­ти наступления хотя бы одного из них (например, в случае трех событий найти вероятность наступления либо одного, ли­бо двух, либо трех событий). Обозначим это событие через А. Справедлива следующая теорема.

ТЕОРЕМА 4. Вероятность появления хотя бы одного из не­зависимых событий А₁, A₂,..., А_n определяется формулой

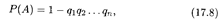
где q_i = 1 — p_i — вероятности соответствующих противо­положных событий 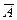_i (i = 1, 2,..., n).

В частном случае, когда все события Аi имеют одинаковую вероятность р, из формулы (17.8) следует, что

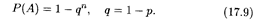
Пример 5. В условиях примера 4 найти вероятность пораже­ния цели (хотя бы одного попадания) при залповой стрельбе орудий.

Решение. Вероятности противоположных событий (про­махов) соответственно равны q ₁ = 0,1, q ₂ = 0,2, q ₃ = 0,3. Иско­мая вероятность находится по формуле (17.8) при п = 3:

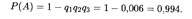
Из этого примера наглядно видно преимущество совместного воздействия случайных событий с целью достижения общего результата.

95. Формула полной вероятности.

Пусть события В ₁, В ₂, …, В_п несовместны и образуют пол­ную группу, т.е., согласно теореме 17.2, выполняется ра­венство

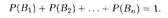
Пусть также событие А может наступить при условии появле­ния одного из событий В_i, причем известны как вероятности P (B_i), так и условные вероятности P_Bi(A) (i = 1, 2,..., п). В таком случае формула для вероятности события А определя­ется следующей теоремой.

ТЕОРЕМА 6. Вероятность события А, появление которо­го возможно лишь при наступлении одного из несовместных событий B_i, образующих полную группу (i = 1, 2,...,п), рав­на сумме попарных произведений каждого из этих событий на соответствующую условную вероятность появления со­бытия А:

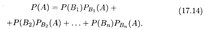
Пример 3. В двух урнах находятся белые и красные шары: в первой — 4 белых и 5 красных, во второй — 7 белых и 3 красных. Из второй урны наудачу взяли шар и переложили его в первую урну. Найти вероятность того, что наудачу взятый после этого из первой урны шар будет белым.

Решение. Перекладывание из второй урны в первую бело­го шара (событие В ₁) и красного шара (событие В ₂) образует полную группу независимых событий. Их вероятности соот­ветственно P(B ₁ ) = 0,7 и Р(В₂) = 0,3. Условные вероятнос­ти извлечения из первой урны белого шара (событие А) при добавлении туда белого или красного шара из второй урны соответственно равны Р_B1(А) = 0,5 и Р_B2(А) = 0,4. Искомая вероятность находится по формуле (17.14) при п = 2:

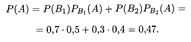
96. Теорема Байеса.

Пусть события B ₁, B ₂,..., В_п несовместны и образуют пол­ную группу, а событие А может наступить при условии появле­ния одного из них. События B_i называют гипотезами, так как заранее неизвестно, какое из них наступит. Пусть произведено испытание и в результате появилось событие А. Тогда оказывается возможным определить условные вероятности гипотез B_i по следующим формулам:

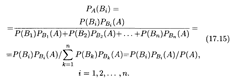
Формулы (17.15) называются формулами Байеса, по имени их автора. Они позволяют оценить вероятность гипотезы В_i во всех испытаниях, где наступает событие А. Иными слова­ми, зная вероятность Р(В_i) до проведения испытания, мы мо­жем переоценить ее после проведения испытания, в результате которого появилось событие А.

Пример 5. Вероятность изготовления изделия с браком равна 0,08. После изготовления все изделия подвергаются проверке, в результате которой изделия без брака признаются годными с вероятностью 0,95, а изделия с браком — с вероятностью 0,06. Найти долю изделий, выпущенных после проверки, а так­же вероятность того, что выпущенное после проверки изделие окажется без брака.

Решение. Независимые события (гипотезы), образующие полную группу, — это B ₁ (изделие без брака) и В ₂ (изделие с браком). Пусть событие А заключается в том, что при проверке изделие признается годным. Ответ на первый вопрос задачи дает формула (17.14):

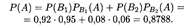
Следовательно, после проверки признаются годными около 88% всех изготовленных изделий.

Ответ на второй вопрос задачи дает формула Байеса (17.15) при п = 2 и i = 1:

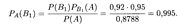
Иными словами, среди изделий, прошедших проверку, содер­жится 99, 5% изделий без брака.

97. Формула Бернулли.

. Если при проведении нескольких испытаний вероятность события А в каждом испытании не зависит от исходов других событий, то эти испытания называются неза­висимыми относительно события А.

Будем рассматривать только такие независимые испыта­ния, в которых событие А имеет одинаковую вероятность. Пусть производится п независимых испытаний, в каждом из которых событие А может появиться с вероятностью р. Тог­да вероятность противоположного события — ненаступления события А — также постоянна в каждом испытании и равна q = 1 - p. В теории вероятностей представляет особый интерес случай, когда в п испытаниях событие А осуществится k раз и не осуществится п - k раз.

Вероятность этого сложного события, состоящего из п ис­пытаний, определяется формулой Бернулли

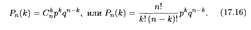
Пример 1. Монету бросают 6 раз. Найти вероятности того, что герб выпадет: 1) 2 раза, 2) не менее двух раз.

Решение. Вероятности выпадения любой из двух сторон монеты одинаковы, т.е. р = q = 0,5. 1) В этом случае п = 6, k = 2. Отсюда согласно формуле (17.16) получаем

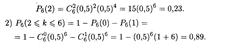
99. Понятие случайной величины. Закон распределения случайной величины. Функция распределения и ее свойства.

. Величину называют случайной, если в ре­зультате испытания она примет лишь одно возможное значе­ние, заранее не известное и зависящее от случайных причин.

Каждой случайной величине соответствует множество чи­сел — это множество значений, которые она может принимать. Например, число мальчиков среди 100 новорожденных — это случайная величина, которая может принимать значения от 0 до 100. Далее будем обозначать случайные величины пропис­ными буквами, а их возможные значения — строчными бук­вами; например, случайная величина Х имеет два возможных значения x ₁ и х ₂. Другой пример: случайная величина Y при­нимает возможные значения, принадлежащие интервалу (а, b). Различают два вида случайных величин.

Определение 2. Случайная величина, принимающая отдельные возможные значения с определенными вероятнос­тями, называется дискретной случайной величиной.

Определение 3. Непрерывной называется случайная величи­на, которая может принимать все значения из некоторого про­межутка.

Закон распределения дискретной случайной величины мож­но изобразить графически, соединив в прямоугольной систе­ме координат ХОР точки (х_i, р_i) отрезками прямых. Так, на рис. 18.1 показан закон распределения из примера 3. Такая фи­гура называется многоугольником распределения.

100. Дискретная случайная величина. Способы задания закона распределения дискретной случайной величины.

Соответствие между отдельными возможны­ми значениями и их вероятностями называется законом рас­пределения дискретной случайной величины.

Как и в случае функциональной зависимости, этот закон можно задать таблицей, аналитически (формулой) и графи­чески. В случае табличного задания закона распределения дис­кретной случайной величины соответствующая таблица состо­ит из двух строк — первая указывает возможные значения, а вторая — их вероятности:

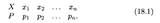
Поскольку в одном испытании случайная величина принимает только одно возможное значение, то события Х = х ₁, Х = х ₂, …, Х = x_п образуют полную группу, т.е. сумма их вероятностей равна единице:

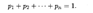
Если множество возможных значений Х дискретной слу­чайной величины бесконечно, то соответствующий ряд веро­ятностей сходится и его сумма равна единице:

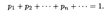
Пример 1. В денежной лотерее на 100 билетов разыгрывается один выигрыш в 20 р., два выигрыша по 10 р. и 10 выигры­шей по 1 р. Найти закон распределения случайной величины Х возможного выигрыша на один билет.

Решение. Возможные значения X: x ₁ = 20, x ₂ = 10, x ₃ = 1, x ₄ = 0. Соответственно их вероятности равны: p ₁ = 0,01, р ₂ = 0,02, р ₃ = 0,1, р ₄ = 1 - (p ₁ +p ₂ + р ₃) = 1 - 0,13 = 0,87. Таким образом, искомый закон распределения имеет вид

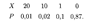
102. Биномиальный закон распределения.

Пусть производится п независимых испытаний и в каждом из них событие А может либо появиться, либо не появиться. Пусть также вероятность р появления события А в каждом ис­пытании постоянна (см. раздел 17.5). В качестве дискретной случайной величины Х рассмотрим число появления события А в этих п испытаниях. Очевидно, что x ₁ = 0, x ₂ = 1, x ₃ = 2,..., x_{n+ 1} = n. Вероятности этих возможных значений k даются фор­мулой Бернулли (см. формулу (17.16)):

где q = 1 - р — вероятность противоположного события (непо­явление события А в одном испытании). Формула (18.2) пред­ставляет собой аналитическую форму закона распределения случайной величины (числа появления события А в n незави­симых испытаниях), которое называется биномиальным. Этот закон получил свое название потому, что правая часть в (18.2) представляет собой общий член разложения бинома Ньютона (17.2). Таким образом, табличная форма биномиального закона с учетом формулы (18.2) имеет вид

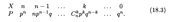
Можно показать, что сумма всех вероятностей второй стро­ки этой таблицы равна единице, т.е.

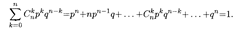
Пример 4. Банк выдает 5 кредитов. Вероятность невозвра­та кредита равна 0,2 для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вер­нувших кредит по окончании срока кредитования.

Решение. Примем за А событие невозврата кредита. Так как заемщики действуют независимо, то выдачу 5 кредитов можно считать за 5 независимых событий. Вероятность невоз­врата k кредитов из 5 описывается биномиальным распределе­нием (18.2), где р = 0,2, q = 0,8, k принимает значения от нуля до 5. Искомая таблица закона распределения составляется, со­гласно (18.3), при п = 5:

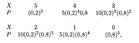
или окончательно:

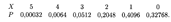
103. Распределение Пуассона

105. Числовые характеристики непрерывной случайной величины.

Определения числовых характеристик дискретных случай­ных величин распространяются и на непрерывные величины. Разница состоит в том, что вместо сумм в формулах (18.5) и (18.10) берутся их интегральные аналоги.

Определение 4. Математическим ожиданием непрерывной случайной величины X, возможные значения которой находят­ся на отрезке [ а, b ], называется определенный интеграл:

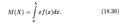
В том случае, когда возможные значения случайной вели­чины Х заполняют всю ось Ох, пределы интегрирования а и b бесконечны: а = - 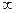, b = 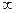. Возможны также случаи, ког­да один из пределов интегрирования бесконечен (возможные значения Х лежат на полупрямой).

Определение 5. Дисперсией непрерывной случайной величины Х называется математическое ожидание квадрата ее отклонения:

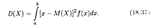
106. Равномерное распределение.

Распределение вероятностей называется рав­номерным, если на интервале возможных значений случайной величины плотность распределения является постоянной.

Пусть на интервале (a, b) плотность распределения являет­ся постоянной величиной: f(x) = С. Определим значение С из условия (18.35):

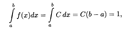
откуда получаем, что f(x) = С = 1/(b - а). Значит, искомая плотность равномерного распределения дается формулой

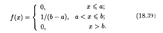
График плотности равномерного распределения указан на рис. 18.5.

107. Показательное распределение.

108. Нормальное распределение. Правило трех сигм.

Общим нормальным распределением вероят­ностей непрерывной случайной величины Х называется рас­пределение с плотностью

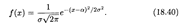
Нормальное распределение задается двумя параметрами: а и σ. Согласно определениям математического ожидания и дисперсии (формулы (18.36) и (18.38)), после выполнения соответствующих интегрирований можно вывести, что для нор­мального распределения справедливы формулы

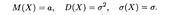
Определение 3. Нормальное распределение с параметрами а = 0 и σ = 1 называется нормированным; его плотность равна

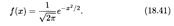
Рассмотрим функцию нормального распределения как пер­вообразную плотности распределения вероятностей. Для слу­чая нормированного нормального распределения (18.41) она, согласно формуле (18.34), имеет вид

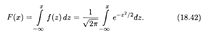
Поскольку функция (18.41) является четной, то неопределен­ный интеграл от нее является нечетной функцией, и потому вместо функции распределения (18.42) используется функция Лапласа (см. п. 17.5)

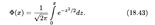
Функции (18.41) и (18.43) табулированы (см. Приложение).

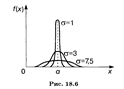
График плотности нормального распределения (18.40) для разных значений а показан на рис. 18.6.

Определение 4. Модой М_о(Х) называется возможное значе­ние случайной величины X, при котором плотность распреде­ления имеет максимум.

Определение 5. Медианой М_е(Х) называется такое возмож­ное значение случайной величины X, что вертикальная пря­мая х = M_e(X) делит пополам площадь, ограниченную кривой плотности распределения.

Нетрудно видеть, что график плотности нормального рас­пределения симметричен относительно прямой х = а, и потому и мода и медиана в данном случае совпадают с математичес­ким ожиданием:

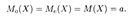
110. Выборочный метод. Задачи математической статистики.

Первой задачей математической статистики является ука­зание методов сбора и группировки статистических сведений, которые получены в результате экспериментов или наблюдений. Вторая задача — это разработка методов анализа статис­тических данных: оценки неизвестных вероятности события, а также функции и параметров распределения; оценка зави­симости случайной величины от других случайных величин; проверка статистических гипотез о виде и величинах пара­метров неизвестного распределения.

На практике сплошное исследование (каждого объекта из интересующей нас совокупности) проводят крайне редко. К то­му же если эта совокупность содержит большое число объек­тов или исследование объекта требует нарушения его функцио­нального стандарта, то сплошное исследование нереально. В таких случаях из всей совокупности случайно отбирают огра­ниченное число объектов и подвергают их исследованию.

Введем основные понятия, связанные с выборками. Гене­ральной совокупностью называется совокупность объектов, из которых производится выборка. Выборочной совокупнос­тью (выборкой) называется совокупность случайно отобран­ных объектов из генеральной совокупности. Число объектов в совокупности называется ее объемом.

Пример 1. Пусть из 2000 изделий отобрано для обследования 100 изделий. Тогда объем генеральной совокупности N = 2000, а объем выборки п = 100.

Выборку можно осуществлять двумя способами. Если пос­ле исследования объект из выборки возвращается в генераль­ную совокупность, то такая выборка называется повторной; если объект не возвращается в генеральную совокупность, то выборка называется бесповторной.

Выборка называется репрезентативной (представитель­ной), если по ее данным можно достаточно уверенно судить об интересующем признаке генеральной совокупности.

111 Генеральная совокупность и выборка. Повторная и бесповторная выборки. Репрезентативная выборка.

Основу статистического исследования составляет множество данных, полученных в результате измерения одного или нескольких признаков. Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений 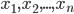случайной величины 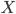, является выборкой, а гипотетически существующая (домысливаемая) — генеральной совокупностью. Генеральная совокупность может быть конечной (число наблюдений N = const) или бесконечной (N = ∞), а выборка из генеральной совокупности — это всегда результат ограниченного ряда 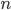наблюдений. Число наблюдений 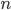, образующих выборку, называется объемом выборки. Если объем выборки 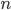достаточно велик (n → ∞) выборка считается большой, в противном случае она называется выборкой ограниченного объема. Выборка считается малой, если при измерении одномерной случайной величины 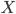объем выборки не превышает 30 (n <= 30), а при измерении одновременно нескольких (k) признаков в многомерном пространстве отношение n к k не превышает 10 (n/k < 10). Выборка образует вариационный ряд, если ее члены являются порядковыми статистиками, т. е. выборочные значения случайной величины Х упорядочены по возрастанию (ранжированы), значения же признака называются вариантами.

Дата добавления: 2015-05-26