Умовний екстремум 4 страница

1)скласти характеристичні рів.

розв’язують його та визнач. Корені і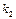

2)якщо і 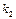дійсні та різні, то заг. роз. рів. має вигляд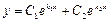

3)якщо 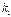= =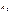k є дійсним числом, то заг. роз. рів. має вигляд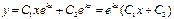

4)якщо 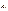і спряжені комплексні числа

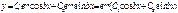
52.Ряд геометричної прогресії. Властивості числових рядів. Необхідна ознака збіжності числового ряду. Гармонічний ряд

Теорема: Якщо ряд збіжний, то: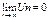

Доведення: Оскільки ряд збіжний, то:

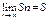
поряд з цією рівністю для збіжного ряду можна записати:

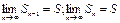
Ця ознака є лише необхідною умовою збіжності. Якщо вона не виконується, то ряд розбіжний, якщо виконується, то ряд може бути як збіжним, так і розбіжним.

53.Ряди Тейлора та Маклорена. Розклад деяких елементарних функцій у ряд

Формули, що подають функцію f (x) у вигляді степеневих рядів, мають вигляд:

(1)

(2)

Кажуть, що ряд Маклорена (1) дає розвинення функції в ряд поблизу точки х = 0, а ряд Тейлора (2) — поблизу точки х = с.

Ряд Маклорена для деяких елементарних функцій:

Область збіжності .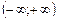

Інтервал збіжності (–1; 1).

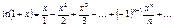Область збіжності (–1; 1).

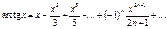Область збіжності [–1; 1].

Використовуючи ці формули, можна у ряді випадків записати розвинення функції в ряд Маклорена без обчислення коефіцієнтів цього ряду (без обчислення похідних функцій).

54. Найб. та найм. значення ф. кількох змінних у замкненій множені.

Функція, що неперервна на замкненій обмеженій множені D досягає на ній найб. та найм. Значення, завжди, цих значень вона може набувати як в середині замкнутій множені,тобто у її внутрішніх точках, так і на її границі, тобто необхідне спеціальне дослідження граничних точок множини D.

Множина наз. замкненою, якщо вона містить усі свої граничні точки, тобто ті точки в околах яких містиця точки які належать і не належать множені.

Множина наз. Обмеженою, якщо вона повністю містиця в середині кола, достатньо великого радіусу.

Найм.(найб.) значення ф. двох незал. змінних неперервної на деякій замкнутій множені наз. глобальним(абсолютним)екстремумом.

Глобальний екстремум ф. досягає у критичній точці, яка належить цій множені або у граничній точці множини.

Алгоритм знаходження глобального екстремуму.

1)Знайти стац.т. в середині множини

2)Знайти стац.т. на границі множини,для цього за допомогою двох змінних звести до ф. однієї змінної

3)Перевірити т. перетину на границі,якщо такі є

4)Знайти значення ф. в усіх стац.т. в середині, на границі множини та в т. перетину, вибрати серед них найб. та найм. значення.

1.Означення функції кількох змінних.
2.Границя та неперервність функції кількох змінних
3.Частинні прирости та похідні функц.кількох змінних
4.Повний диференціал функції кількох змінних
5.Застосування повного диференціалу для обчислення наближених
6.Похідна у заданому напрямку
7.Градієнт
8.Частині похідні вищих порядків
9.Означення екстремуму функції кількох незалежних змінних.Необхідна та достатня умова існування екстремуму
10.Дослідження функції 2 змінних на екстремум
11.Найбільше та найменше значення функції у замкненій множині
12.Умовний екстремум
13.Задачі диференціювання та інтегрування.означення первісної.теорема про множину первісних
14.Невизначений інтеграл, властивості
15.Інтегрування невизначеного інтегралу замінною змінних
16.Інтегрування нев.інтегралу частинами
17.Інтегрування найпростіших раціональних функцій
18.Інтегрування деяких ірраціон.функцій
19.Інтегрування довільної раціональної функції
20.Інтегрування тригоном.функцій
21.Визначений інтеграл як границя інтегральної суми
22.Формула Ньютона-Лейбніца
23.Геометричний зміст визначеного інтеграла
24.Метод обчислення визначеного інт.
25.Властивість визначеного інтегралу
26.Властивість невизначеного інтеграла
27.Невласні інтеграли з нескінченними множинами інтегрування(першого роду)
28.Означення збіжності невласних інтегралів першого роду
29.Невласні інтеграли від необмежених функцій(другого роду)
30.Наближене обчислення визначених інтегралів
31.Означення числового ряду.сума числового ряду.
32.Властивості рядів.збіжність ряду
33.Умови збіжності додатного ряду
34.Знакозмінні ряди.ознака Лейбніца
35.Абсолютно та умовно збіжні ряди
36.Функціональні ряди.основні поняття
37.Степеневі ряди.ознака Абеля.радіус збіжності степеневого ряду
38.Теорему про рівномірну збіжність степеневого ряду
39.Розклад функцій у степеневий ряд
40.Розклад функції у ряд Маклорена
41.Розклад ф.у ряд Тейлора
42.Розклад ф.у ряд Фур’є
43.Лінії рівня функції кількох змінних.означення, приклади.
44.Використання універсальної підстановки при інтегруванні тригонометричних виразів
45.Метод невизначених коефіцієнтів
46.Поняття диф.рівняння та його розв’язку
47.Теорема коші про інтегрування та єдиність розв’язку рівняння першого порядку
48.Рівняння з відокремленими змінними
49.Однорідні диф.рівняння
50.Лінійні диф.рівняння
51.Лінійні диф.рівняння другого порядку зі сталими коефіцієнтами
52.Ряд геометричної прогресії.властивості числових рядів.необхідна ознака збіжності числового ряду.гармонійний ряд.
53.Ряди Тейлора і Маклорена.розклад деяких елементарних функцій у ряд
54.Найбільше та найменше значення функції кількох змінних у замкненій множині.

Дата добавления: 2015-05-26