Основные виды граничных условий

2.1 Начальные условия краевых задач теплопроводности

Начальные условия обычно задаются в виде известных значений температурного поля внутри исследуемого образца в момент времени, предшествующий (или совпадающий) с моментом подачи теплового воздействия на образец, например: T (x, y, z, 0) = T _н(x, y, z); T (x, 0) = T _н (x)

Для упрощения получающихся аналитических решений стараются обеспечить, чтобы начальные условия имели простейший вид, например: Т _н (x, y, z) = T _н = const или T _н(x) = T _н = const.

2.2 Граничные условия краевых задач теплопроводности

Граничные условия могут быть заданы в виде граничных условий первого, второго, третьего или четвертого рода.

Граничные условия первого рода обычно задают в виде известного закона изменения во времени температуры на поверхности исследуемого образца. Для тела, представленного на рис., граничные условия первого рода (ГУ-1) имеют вид: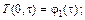

Функции 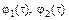могут иметь вид: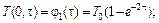

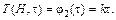
В общем случае граничные условия имеют вид: 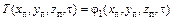, где 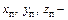координаты точек поверхности тела.

Граничные условия второго рода обычно задают в виде известных функций изменения во времени теплового потока на поверхности тела. С учетом закона Фурье 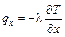для случая геометрии образца, представленного на рис., получаем запись граничных условий второго рода (ГУ-2) в виде

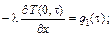
В простейшем случае:

Эти функции могут быть записаны в виде:

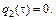
Граничные условия третьего рода описывают взаимодействие тела с окружающей средой по закону конвективного теплообмена, предложенного Ньютоном и имеющим вид: ,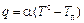

где a – коэффициент теплообмена [Вт/(м² °С)]; 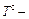температура греющей среды; Т _п – температура поверхности.

С учетом того что , для случая геометрии образца, представленного на рис, получаем запись граничных условий третьего рода (ГУ-3) в виде:

, .

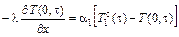Граничные условия четвертого рода задаются (см. рис. 1.3, в) на внутренних границах контакта двух твердых тел или на границах контакта твердое тело – жидкость (газ) следующим образом:

Согласно граничным условиям четвертого рода (ГУ-4) на границе контакта обеспечивается одновременная непрерывность изменения как температур, так и тепловых потоков, хотя производные температурного поля по координате при этом могут иметь разрыв

В некоторых случаях на практике используют граничные условия четвертого рода специального вида [2], учитывающие наличие поверхностного источника тепла р (t) [Вт/м²], действующего на поверхности раздела соседних слоев. Например, в случае, если на поверхности x = h будет действовать источник тепла с удельной поверхностной мощностью р (t), то ГУ-4 специального вида могут быть записаны в виде:

Дата добавления: 2015-05-26