Введение в планирование эксперимента

И обработка результатов

Планирование

теплотехнического эксперимента

Учебное пособие

Печатается в авторской редакции

Формат 60´84 ¹/₁₆. Бумага офсетная. Печать цифровая

Усл. печ. л. 4,95. Уч.-изд. л. 4,5. Тираж 25. Заказ 212.

Южно-Российский государственный технический университет (НПИ)

Отпечатано в типографии НГМА

346428, г. Новочеркасск, ул. Пушкинская, 111.

Различают следующие виды экспериментов:

Пассивный эксперимент (наблюдение) – проводится в ходе обычного функционирования изучаемого объекта.

Активным называют эксперимент, в ходе которого исследователь сам назначает режимы работы исследуемого объекта.

Натурный эксперимент проводится непосредственно на исследуемом объекте. Его достоинством является высокая достоверность, однако он не всегда осуществим из-за сложности, энергоемкости, высокой стоимости, невозможности работы в области критических нагрузок и в аварийных режимах и т.п.

Физическая модель воспроизводит изучаемый объект с сохранением его физической природы, основных его свойств и с соблюдением условий подобия.

Математическая модель – это математическое описание объекта и его свойств, существенных для рассматриваемого взаимодействия с окружающей средой.

Изучаемый объект характеризуется n параметрами. Для определения в результате эксперимента зависимостей между этими параметрами необходимо их разделить на две группы:

· независимые переменные (факторы), значениями которых задаются в эксперименте (x_j, );

· зависимые переменные (отклики), значения которых измеряются в процессе проведения опытов (y_i, ).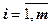

Целью проведения экспериментов является нахождение функций отклика, т.е. зависимостей 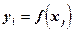. Для ее достижения необходимо выполнить:

· планирование эксперимента;

· проведение эксперимента и получение экспериментальных данных;

· обработку данных, т.е. получение функциональных зависимостей между параметрами.

Выбор вида функциональной зависимости – задача не формализуемая, т.к. одна и та же кривая на некотором участке примерно с одинаковой точностью может быть описана самыми различными аналитическими выражениями.

Для рационального выбора вида аналитической зависимости необходимо учитывать ряд требований:

· удобство ее последующего использования;

· компактность;

· ее содержательность (интерпретируемость, возможность придания определенного физического смысла константам уравнения или функциям).

Таким образом, принятие решения о выборе вида аналитической зависимости остается за исследователем.

Если выбор вида аппроксимирующей функции процесс не формализуемый, то расчет параметров (коэффициентов) выбранной функции – операция чисто формальная и ее следует осуществлять на компьютере.

В общем случае этот расчет состоит в решении системы нелинейных уравнений. В частных случаях это может быть система уравнений, линейных относительно искомых коэффициентов, или система уравнений, которые после преобразования сводятся к линейным уравнениям относительно коэффициентов.

Например, если в результате проведения n опытов известны значения x_i и y_i (), а для аппроксимации выбрана модель в виде полинома

,

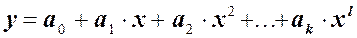то расчет неизвестных коэффициентов сводится к решению системы уравнений, линейных относительно них.

.

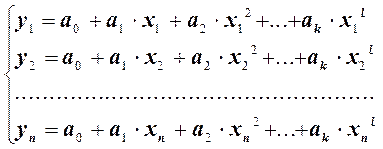Если для аппроксимации принята модель вида

,

то после ее линеаризации (в данном случае выполнив операцию логарифмирования) получим

,

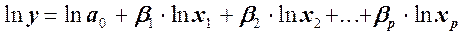или после замены переменных 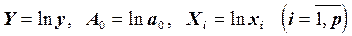придем к линейной зависимости .

Из приведенных примеров видно, что число независимых уравнений системы равно числу поставленных опытов. С другой стороны, для определения k коэффициентов необходимо не менее k независимых уравнений. Но если число n поставленных опытов и число независимых уравнений равно числу искомых коэффициентов, то решение системы единственно, а, следовательно, случайно, т.к. результаты отдельных опытов (x_i и y_i) случайны из-за наличия погрешностей (инструментальных, методических, систематических, случайных).

При числе опытов n большем, чем число искомых коэффициентов k, число независимых уравнений системы избыточно. Из этих уравнений можно составить несколько систем уравнений, каждая из которых в отдельности даст свое решение. Но между собой эти решения будут несовместны. Если их все построить на графике, то получим пучок аппроксимирующих кривых.

Это открывает (при n>k) следующие возможности:

· этот пучок кривых показывает форму и ширину области неопределенности проведенного эксперимента;

· можно провести усреднение всех найденных кривых. Полученная усредненная кривая будет гораздо точнее и достовернее описывать исследованное явление, т.к. она в значительной степени освобождена от случайных погрешностей, приведших к разбросу отдельных экспериментальных точек.

Усреднение несовместных решений избыточной системы уравнений может быть произведено методом регрессионного анализа (методом наименьших квадратов МНК), разработанным Лежандром и Гауссом в 1795–1805 г.г.

Сущность метода. После предварительного анализа (сбора априорной информации) должна быть выбрана модель, например вида

.

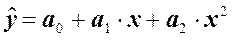Теперь задача состоит лишь в том, чтобы найти наилучшие значения параметров модели а₀, а₁, а₂. Значения же x_i и y_i, наоборот, нам известны. Это не переменные, а конкретные числа, полученные в результате проведения опытов. Поэтому любая функция от x (будь то x², l n x, x^1/2...) при известном x – это тоже известное, в данном случае, число. Для рассматриваемого примера введем следующие обозначения x=x₁ и x²=x₂. Тогда модель примет вид .

Между рассчитанными по модели значениями и экспериментальными значениями y_i будут наблюдаться отклонения .

Метод наименьших квадратов позволяет найти такие значения искомых параметров а₀, а₁, а₂, при которых сумма квадратов отклонений, взятая по всем точкам, будет минимальна

.

Если это описать формально, т.е. взять поочередно частные производные по а₀, а₁, а₂ и приравнять их к нулю, то получим систему уравнений, решением которой будут искомые коэффициенты а₀, а₁, а₂.

Итак, ,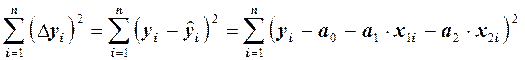

производные по а₀, а₁, а₂ имеют вид:

.

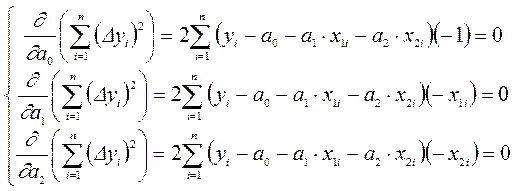Полная система уравнений для расчета параметров рассматриваемой модели будет:

.

По введенным экспериментальным данным (x_i и y_i) любая программа для решения системы линейных уравнений выдаст численные значения искомых коэффициентов.

Линия, определенная по методу наименьших квадратов, называется линией регрессии, а коэффициенты а₀, а₁, а₂ и т.д. – коэффициентами регрессии y по x.

Дата добавления: 2015-05-26