В линейном пространстве

Линейная зависимость и независимость системы векторов

Определение 1.4. Система векторов 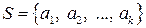линейного пространства 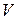называется линейно зависимой, если существуют числа 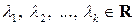, среди которых есть хотя бы одно отличное от нуля, причем выполняется равенство

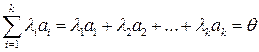. (1.2)

Определение 1.5. Система векторов 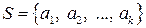линейного пространства 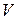называется линейно независимой, если равенство (1.2) выполняется только при значениях 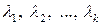, равных нулю одновременно.

Опуская слово “система”, часто говорят: векторы 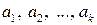линейно зависимы или соответственно линейно независимы.

Определение 1.6. Подсистемой системы векторов 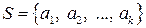называется любое множество векторов, каждый вектор которой принадлежит системе .

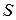Определение 1.7. Линейной оболочкой

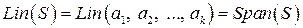
системы векторов 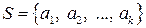называется множество, состоящее из всевозможных линейных комбинаций векторов системы :

.

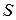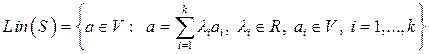Линейная оболочка 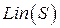состоит из всех векторов 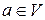, линейно выраженных через векторы системы .

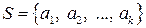Определение 1.8. Рангом 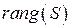системы векторов 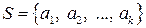называется максимальное число линейно независимых векторов в .

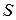Рассмотрим основные свойства линейно зависимых и линейно независимых систем векторов в линейном пространстве.

Свойство 1.1. Система 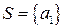, состоящая из одного вектора 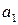является линейно зависимой (линейно независимой) тогда и только тогда, когда этот вектор нулевой (соответственно ненулевой).

□ В самом деле, пусть система 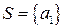линейно зависима. Тогда существует число 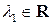, такое, что выполняется равенство

,

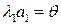откуда следует, что .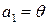

Обратно, если вектор 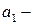нулевой (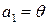), то равенство (1.2) имеет место при любом 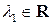, в том числе для любого , откуда по определению следует, что система 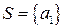линейно зависима.

Доказательство свойства в случае линейной независимости системы проводится аналогично. ■

Свойство 1.2. Если какая-то подсистема для системы 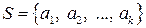является линейно зависимой, то и вся система 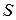является линейно зависимой (из линейной зависимости какой-нибудь подсистемы следует линейная зависимость всей системы).

□Предположим без ограничения общности, что подсистема

()

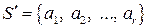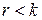системы 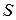является линейно зависимой, то есть если существуют числа 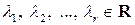, среди которых есть хотя бы одно отличное от нуля, причем выполняется равенство

.

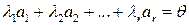Дополнив левую часть последнего равенства суммой 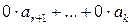(которая не изменит равенства линейной комбинации нулевому вектору), получим

.

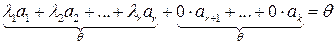Заключаем, что существует набор чисел

,

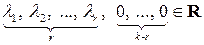среди которых есть хотя бы одно отличное от нуля (оно обязательно встречается среди чисел 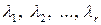), причем такой, что линейная комбинация системы векторов 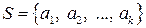равна нулевому вектору. По определению система 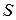является линейно зависимой. ■

Свойство 1.3. Если система 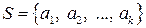является линейно независимой, то и любая ее подсистема также является линейно независимой (из линейной независимости системы следует линейная независимость любой подсистемы).

□Это свойство является эквивалентом предыдущего. Действительно, система, имеющая линейно зависимую подсистему, не может быть сама линейно независимой. Поэтому у линейно независимой системы вообще не может быть линейно зависимых подсистем. ■

Свойство 1.4. Система векторов 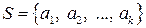является линейно зависимой тогда и только тогда, когда некоторый вектор 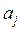(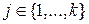), входящий в состав 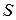, есть линейная комбинация остальных векторов этой системы:

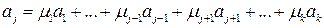. (1.3)

□Необходимость. Пусть система векторов 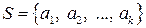является линейно зависимой. Тогда существуют числа 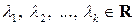, среди которых есть хотя бы одно отличное от нуля (предположим для определенности, что при некотором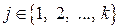 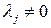), причем выполняется равенство

.

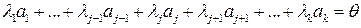Выразив из последнего равенства вектор 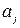, получим

,

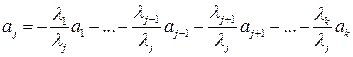откуда и следует справедливость равенства (1.3) при ().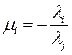

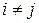Достаточность. Пусть выполняется равенство (1.3). Перенеся вектор 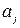в правую часть, получим

,

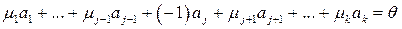откуда следует, что существует набор чисел 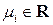(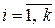), среди которых есть хотя бы один ненулевой (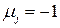), причем такой, что линейная комбинация векторов системы 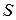с коэффициентами 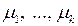равна нулевому вектору. При этом система 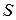векторов является линейно зависимой. ■

Свойство 1.5. Пусть система векторов 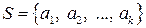является линейно независимой, а система 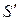векторов получается из системы 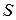присоединением к ней вектора :

.

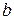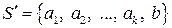Тогда система векторов 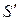является линейно зависимой тогда и только тогда, когда вектор .

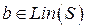□ Необходимость. Пусть система 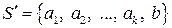является линейно зависимой. Тогда существуют числа 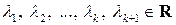, среди которых есть хотя бы одно отличное от нуля (причем обязательно 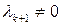, объяснить почему) причем выполняется равенство

.

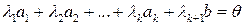Выразив из последнего равенства вектор 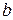в виде линейной комбинации векторов системы 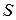с коэффициентами 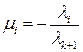(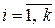), получаем, что вектор .

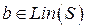Достаточность доказывается аналогично. ■

Свойство 1.6. Пусть система векторов 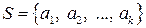является линейно независимой. Тогда разложение вектора 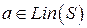в виде (1.1) определено однозначно (существует единственный набор коэффициентов 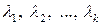разложения (1.1)).

□Справедливость данного свойства доказывается методом от противного. Предположим, что помимо разложения (1.1) существует аналогичное разложение с другим набором коэффициентов :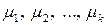

.

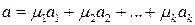Вычтя из последнего равенства равенство (1.1), получим

.

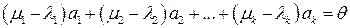Так как система векторов 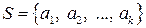является линейно независимой, то при всех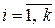 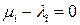, откуда следует единственность набора коэффициентов . ■

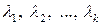Свойство 1.7. Пусть задана система векторов 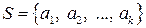, причем 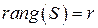, 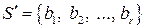– ее подсистема, являющаяся линейно независимой (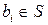, 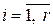). Тогда любой вектор 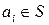(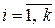) может представлен в виде линейной комбинации через векторы системы 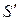единственным образом.

□ Данное свойство является обобщением предыдущего свойства. Нетрудно убедиться, что 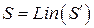. Тогда по свойству 1.6 любой вектор 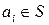(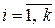) единственным образом представляется в виде линейной комбинации через векторы системы :

().

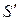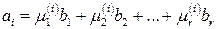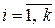Свойство 1.8. Если система векторов 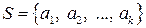является линейно независимой и вектор 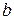не является их линейной комбинацией (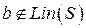), то расширенная система векторов 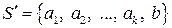также является линейно независимой.

□Для доказательства составим равенство

.

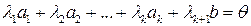Коэффициент 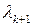равен нулю, так как в противном случае 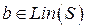. Тогда последнее равенство примет вид

,

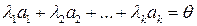откуда вследствие линейной независимости системы 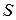следует, что при всех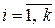 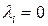. При этом система 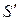является линейно независимой. ■

Дата добавления: 2015-05-29