Исследование на линейную зависимость систем многочленов

Алгоритмы исследования на линейную зависимость систем векторов

Рассмотрим на примерах конкретных линейных пространств (пространство многочленов 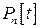и пространство матриц 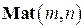) вопрос об исследовании системы векторов на линейную зависимость.

Пусть дана система многочленов в линейном пространстве :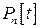

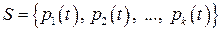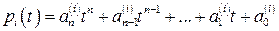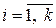, (). (1.4)

Для исследования на линейную зависимость систему (1.4) составляем равенство вида (1.2) для определения весовых коэффициентов :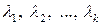

().

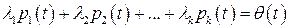
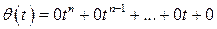Записав последнее равенство в координатной форме, получим

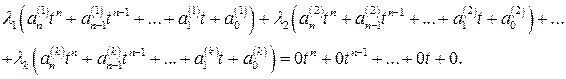
Приравнивая коэффициенты при одинаковых степенях переменной 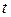в левой и правой частях этого равенства, получим ОСЛАУ для определения коэффициентов 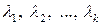разложения:

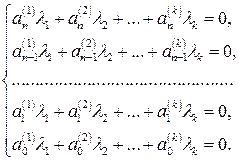(1.5)

Обозначим через 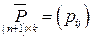основную матрицу системы (1.5) размера 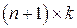(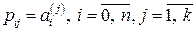), 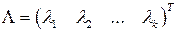вектор-столбец весовых коэффициентов. Тогда систему (1.5) можно записать в матричной форме

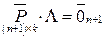. (1.6)

Известно, что если 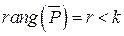, то система (1.6) имеет ненулевые решения относительно вектор-столбца 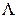. Это означает, что система (1.6) имеет ненулевые решения относительно весовых коэффициентов 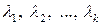. При этом система многочленов (1.4) является линейно зависимой и ее .

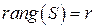Пример 1.1. Исследовать на линейную зависимость и найти ранг системы многочленов :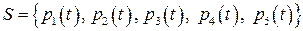

, ,

, .

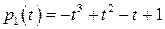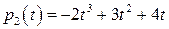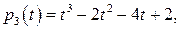
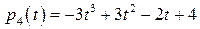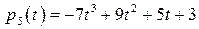В случае линейной зависимости найти подсистему 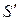, являющуюся линейно независимой. Выразить векторы через векторы подсистемы .

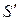Решение. Составим равенство (1.2):

.

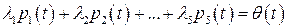Запишем систему вида (1.5) с основной матрицей :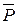

.

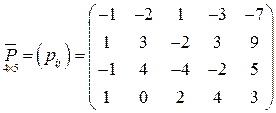После приведения матрицы 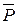к ступенчатому виду при помощи метода Жордана-Гаусса (в результате элементарных преобразований нумерация столбцов осталась прежней), получим

.

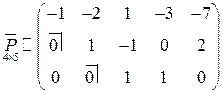Перейдем от ступенчатой матрицы к системе уравнений. Получим

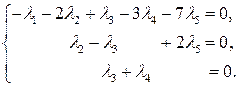
Так как 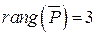, то выберем за базисные (основные) переменные 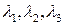, за свободные – переменные 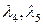. Выражая базисные переменные через свободные, получим общее решение ОСЛАУ

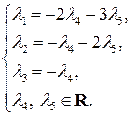
Так как 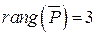, то 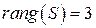, следовательно, рассматриваемая система многочленов линейно зависима. В качестве линейно независимой подсистемы примем 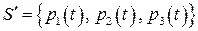. Тогда остальные векторы 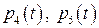можно выразить через векторы подсистемы 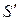. Положив 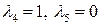, получим 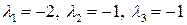. Тогда из равенства (1.2) следует, что

.

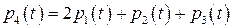Аналогично взяв 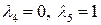, получим 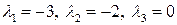и

.

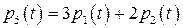Дата добавления: 2015-05-29