Формулы преобразования координат

Переход от базиса к базису, свойства матрицы перехода.

За исключением некоторых случаев в линейном пространстве существует более одного базиса. Возникает задача получить формулы связи между двумя базисами. Пусть даны два базиса в пространстве ():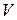

,

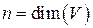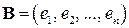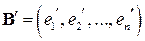
Первый базис условно назовем “старым”, второй 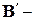“новым”.

Каждый вектор (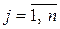) базиса разложим по векторам 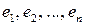базиса в виде

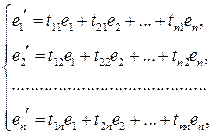
или в матричной форме

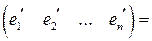
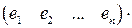
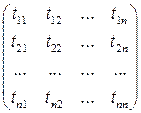. (1.14)

Определение 1.12. Формула (1.14) называется формулой перехода от базиса к базису . Ее удобно записать в виде

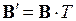. (1.15)

При этом матрица 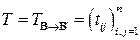называется матрицей перехода от базиса к базису .

Заметим, что столбцами матрицы 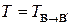являются координатные вектор-столбцы, соответствующие векторам нового базиса в старом базисе .

Рассмотрим основные свойства матрицы перехода.

Теорема 1.4 (свойства матрицы перехода).

1. Матрица перехода от базиса к базису есть единичная матрица.

2. Всякая матрица 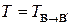перехода от базиса к базису является неособенной, причем 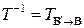есть матрица перехода от базиса к базису .

3. Пусть , , 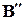– базисы в 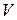. Если 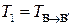, 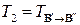– матрицы перехода от к и от к 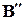соответственно, то 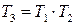– матрица перехода от к .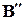

4. Пусть , , 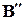– базисы в 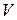. Если 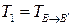, 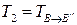– матрицы перехода от к и от к 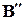соответственно, то 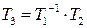– матрица перехода от к .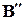

□ 1. Положив в формуле (1.15) 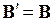, получим 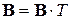, откуда следует, что матрица перехода .

2. Предположим, что матрица 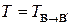перехода от базиса к базису является особенной. Тогда по свойству определителей столбцы матрицы 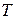линейно зависимы. Учитывая, что столбцами матрицы 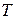являются координатные вектор-столбцы

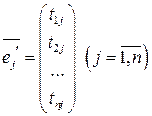
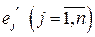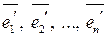векторов базиса в базисе , то система вектор-столбцов линейно зависима. Следовательно, линейно зависима система 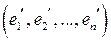, что противоречит тому, что 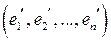является базисом.

3. Если 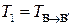, 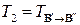есть матрицы перехода от к и от к 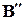соответственно, то на основании формулы (1.15) имеем

,

откуда

,

то есть 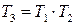– матрица перехода от к .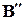

4. Если 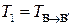, 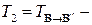матрицы перехода от к и от к 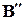соответственно, то на основании формулы (1.15) имеем

,

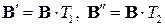откуда (учитываем, что )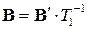

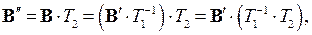
то есть 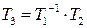является матрицей перехода от к . ■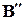

Следующая теорема дает критерий того, является ли конкретная система векторов базисом линейного пространства.

Теорема 1.5. Пусть 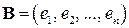– базис в 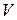, 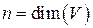. Рассмотрим систему векторов 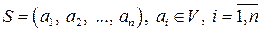. Разложим вектор 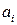(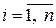) по векторам базиса :

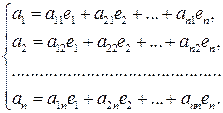
Из коэффициентов разложений составим матрицу .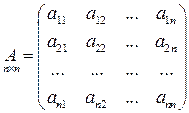

Тогда система векторов 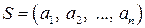является базисом в пространстве 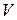тогда и только тогда, когда матрица 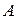является неособенной матрицей.

Рассмотрим изменение координатного вектор-столбца одного и того же вектора при переходе от одного базиса к другому.

Теорема 1.6. Пусть

,

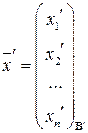
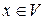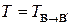есть координатные вектор-столбцы вектора в базисах и соответственно (). Тогда

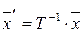. (1.16)

□ Разложим вектор 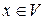по векторам базисов и . Используя формулу (1.10), получим 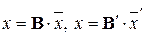. Приравнивая правые части последних равенств, получим 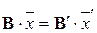. Учитывая связь между базисами и (формула (1.15)), имеем .

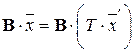Последнее равенство можно рассматривать как запись двух разложений одного и того же вектора 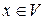в базисе . Разложениям соответствуют вектор-столбцы 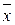и 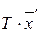. Так разложение вектора по базису единственно (см. теорему 1.1), то 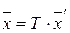, откуда и получаем равенство (1.16). ■

Согласно теореме 1.6, чтобы получить координатный вектор-столбец вектора в новом базисе , необходимо матрицу перехода от нового базиса к старому умножить на координатный вектор-столбец вектора в старом базисе .

Определение 1.13. Равенство (1.16) называется формулами преобразования координат при переходе от базиса к базису .

Рассмотрим далее на примерах пространств 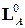и 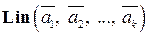алгоритмы перехода от базиса к базису.

Дата добавления: 2015-05-29