
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В евклидовом пространстве
|
|
|
|
Процесс ортогонализации Грамма-Шмидта системы векторов
Для дальнейшего изучения евклидовых пространств важно уметь строить в этих пространствах ортонормированные базисы. Как будет показано в следующей теореме, по произвольному базису евклидова пространства всегда можно построить ортонормированный базис.
Теорема 3.6. В любом конечномерном евклидовом пространстве существует ортонормированный базис.
□ Выберем произвольный базис  в
в 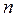 -мерном евклидовом пространстве
-мерном евклидовом пространстве 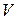 . Существование искомого ортонормированного базиса
. Существование искомого ортонормированного базиса 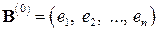 в пространстве
в пространстве 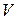 докажем его построением.
докажем его построением.
На первом шаге положим векторы 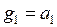 ,
,  , причем
, причем 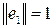 .
.
На втором шаге построим вектор 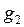 так, чтобы он был ортогонален вектору
так, чтобы он был ортогонален вектору 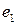 . Подберем его в виде
. Подберем его в виде
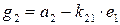 .
.
Из условия ортогональности векторов 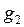 и
и 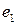 получим
получим
 ,
,
откуда 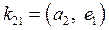 . Итак, вектор
. Итак, вектор 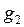 имеет вид
имеет вид
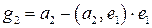 .
.
Пронормировав его, получим единичный вектор 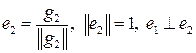 .
.
На третьем шаге строим вектор
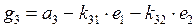
так, чтобы он был ортогонален векторам 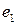 и
и 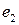 . Из условия ортогональности векторов
. Из условия ортогональности векторов 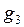 и
и 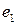 ,
, 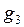 и
и 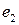 получим
получим
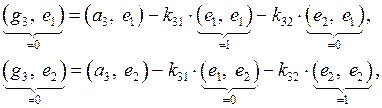
откуда 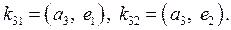 Итак, вектор
Итак, вектор 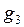 имеет вид
имеет вид
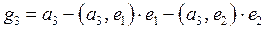 .
.
Пронормировав его, получим единичный вектор 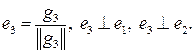
Продолжая процесс построения векторов 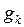 (
(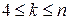 ) при условии, что
) при условии, что 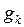 ортогонален векторам
ортогонален векторам 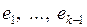 , получим
, получим
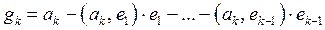 ,
,

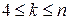 .
.
В силу того, что построенные векторы 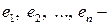 единичные и попарно ортогональные (а значит, линейно независимые), то они образуют ортонормированный базис
единичные и попарно ортогональные (а значит, линейно независимые), то они образуют ортонормированный базис 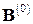 евклидового пространства. ■
евклидового пространства. ■
Рассмотренный выше процесс построения ортонормированного базиса 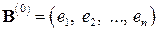 по произвольному базису
по произвольному базису  называют процессом ортогонализации Грама-Шмидта. Итак, процесс ортогонализации заключается в последовательном вычислении следующих векторов:
называют процессом ортогонализации Грама-Шмидта. Итак, процесс ортогонализации заключается в последовательном вычислении следующих векторов:
| Составление ортогонального базиса | Процесс нормировки, получение ортонормированного базиса | Условия ортогональности векторов |
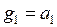
| 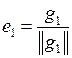 , , 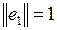
| |
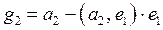
| 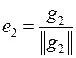 , , 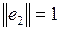
| 
|
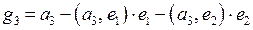
| 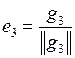 , , 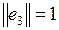
| 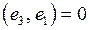 , ,
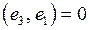
|
| …………………………………… | …………….…………… | ………………… |
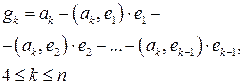
| 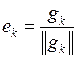 , ,  , ,
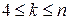
| 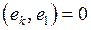 ,
……………. ,
…………….
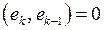
|
Рассмотрим на примере процесс ортогонализации Грамма-Шмидта.
Пример 3.2. В пространстве  со стандартным скалярным произведением
со стандартным скалярным произведением 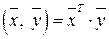 задан базис
задан базис 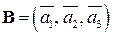 :
:
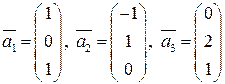 .
.
Провести процесс ортогонализации Грама-Шмидта системы векторов базиса 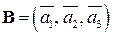 .
.
Решение. Проведем процесс ортогонализации Грама-Шмидта системы векторов 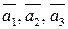 базиса
базиса 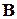 . Согласно предложенной методике решения задачи вычисляем следующие векторы:
. Согласно предложенной методике решения задачи вычисляем следующие векторы:
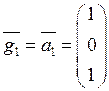 ,
,  ,
, 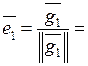
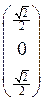 ,
, 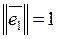 ;
;
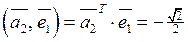 ,
, 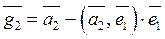
 ,
,
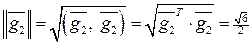 ,
, 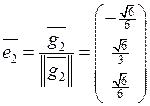 ,
, 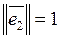 ;
;
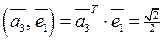 ,
, 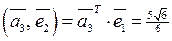 ,
,
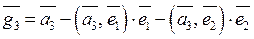
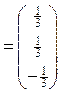 ,
, 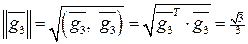 ,
,
 ,
, 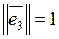 .
.
Итак, ортонормированный базис 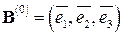 состоит из векторов:
состоит из векторов:
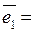
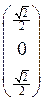 ,
,  ,
, 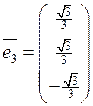 .
.
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 676; Нарушение авторских прав?; Мы поможем в написании вашей работы!