Расчет параметров объекта управления

Существуют аналитические, экспериментальные и комбинированные методы получения математического описания объектов управления.

Аналитические методы базируются на использовании уравнений, описывающих физико-химические и энергетические процессы, протекающие в исследуемом объекте управления. Это, например, законы сохранения вещества и энергии (уравнения материального баланса). В настоящее время для многих классов объектов управления получены их математические модели. В частности, для аэрокосмических объектов (ракет, самолетов, вертолетов), для технологических объектов (химические реакторы), для энергетических процессов (ядерные реакторы, паровые турбины, генераторы, двигатели). При получении таких описаний обычно оперируют с дифференциальными уравнениями в частных производных, так как переменные изменяются и во времени, и в пространстве.

Экспериментальные методы предполагают проведение серии экспериментов на реальном объекте управления. Обработав результаты экспериментов, оценивают параметры динамической модели объекта, задавшись предварительно ее структурой.

Наиболее эффективными оказываются комбинированные методы построения математической модели объекта, когда, используя аналитически полученную структуру объекта, ее параметры определяют в ходе натурных экспериментов.

Для быстрого и экономичного определения динамических характеристик обычно используют метод переходных характеристик (кривых разгона). В режиме ручного управления подают ступенчатое входное воздействие (1–5 % от диапазона регулирования) и регистрируют изменение выходного сигнала.

При проведении эксперимента обычно требуется для достоверности снять 4–16 переходных характеристик (в зависимости от помех), затем каждую характеристику обработать (произвести сглаживание переходной характеристики, например, скользящим усреднителем), нормировать, усреднить до одной и аппроксимировать.

Сняв кривую разгона и оценив характер объекта управления (с самовыравниванием или без), можно определить параметры соответствующей передаточной функции. Перед началом обработки кривую разгона рекомендуется пронормировать (диапазон изменения нормированной кривой 0–1) и выделить из ее начального участка величину чистого временного запаздывания.

При снятии кривой разгона необходимо выполнить ряд условий:

1. Если проектируется система стабилизации, то кривая разгона должна сниматься в окрестности рабочей точки процесса.

2. Кривые разгона необходимо снимать как при положительных, так и отрицательных скачках управляющего сигнала. По виду кривых можно судить о степени асимметрии объекта. При небольшой асимметрии расчет настроек регулятора рекомендуется вести по усредненным значениям параметров передаточных функций. Линейная асимметрия наиболее часто проявляется в тепловых объектах управления.

3. При наличии зашумленного выхода желательно снимать несколько кривых разгона с их последующим наложением друг на друга и получением усредненной кривой.

4. При снятии кривой разгона необходимо выбирать наиболее стабильные режимы процесса, например ночные смены, когда действие внешних случайных возмущений маловероятно.

5. При снятии кривой разгона амплитуда пробного входного сигнала должна быть, с одной стороны, достаточно большой, чтобы четко выделялась кривая разгона на фоне шумов, а с другой стороны, она должна быть достаточно малой, чтобы не нарушать нормальный ход технологического процесса.

В простейшем случае при практических расчетах наиболее часто h (t) объекта аппроксимируют либо апериодическим звеном с запаздыванием (рис. 14.22, а),

,

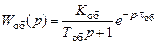либо интегрирующим звеном с запаздыванием (рис. 14.22, б),

.

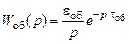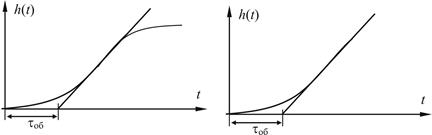
а б

Рис. 14.22. Аппроксимация объекта регулирования

Рассмотрим пример. Построим график нормированной кривой разгона по ее значениям, приведенным ниже (выделена величина чистого запаздывания τ_з = 3 мин).

t, мин
h		0,087	0,255	0,43	0,58	0,7	0,78	0,84	00,92	00,96

Определение динамических характеристик объектов по кривой разгона можно производить разными методами.

Метод касательной к точке перегиба кривой разгона. В данном случае точка перегиба соответствует переходу кривой от режима ускорения к режиму замедления темпа нарастания выходного сигнала. Полное запаздывание τ_об определяется в соответствии с графиком τ_об = τ_з + τ _d.

Формульный метод позволяет аналитически вычислить величину динамического запаздывания и постоянной времени по формуле

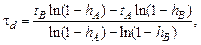
где значение 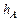берется в окрестности точки перегиба кривой, а значение 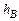принимается равным 0,8–0,85. По этим значениям определяются и моменты времен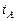и и .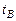

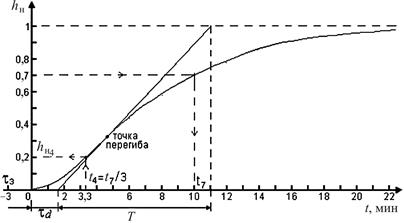
Рис. 14.23. График кривой разгона

Тогда

.

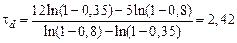Близкие результаты получаются по методу Круг–Мининой:

t_об = 0,5(3t₁ – t₂), Т _об = 1,25(t₂ – t₁),

где t₁ – время при h (t) = 0,33H_уст, t₂ – время при h (t) = 0,7H_уст.

Методика определения параметра K динамической модели объекта без самовыравнивания 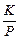рассмотрим на примере кривой разгона регулирования нагрузки осветлителя. Предполагается, что на вход объекта увеличили подачу воды на 10 м³/час = D G, при этом уровень начал увеличиваться. Приращение уровня зафиксировано ниже.

tc, с
D h, мм

Для объекта без самовыравнивания коэффициент усиления определяется как отношение установившейся скорости изменения выходной величины к величине скачка входного сигнала (рис. 14.24):

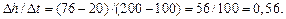
K = 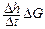= 0,56/10 = 0,056.

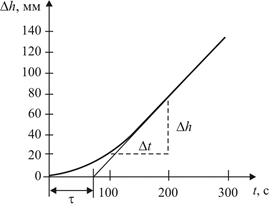
Рис. 14.24. График разгонной характеристики объекта
без самовыравнивания

Объект можно более точно описать передаточной функцией 2-го порядка, выводимой из реальной кривой разгона (рис. 14.25):

.

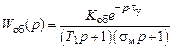Т ₁ можно найти, если отрезок ab разделить пополам, найдя точку с, от­куда Т ₁ = DB.

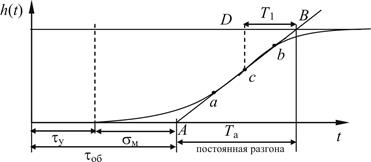
Рис. 14.25. Реальная кривая разгона

Уже затем для расчетов принимают

,

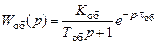где t_об = t_у + s_м, Т _об = Т ₁ + s_м. Ориентировочно можно принять Т _об = Т _а.

На рис. 14.26 представлены экспериментальная кривая 1 и аппроксимированная кривая 2 по уравнению звена первого порядка с запаздыванием. Хотя кривые отличаются, все же такое представление наиболее распространено из-за простоты и удобства в расчетах.

Существенно лучше сближение переходных характеристик может быть получено при аппроксимации объекта последовательным соединением двух звеньев первого порядка с одинаковыми постоянными времени Т ₂ (кривая 3 на рис. 14.26).

,

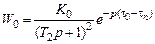где Т ₂ = Т ₀ / 2,72, τ _n = 0,102 Т ₀.

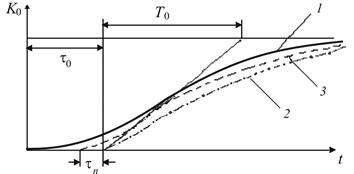
Рис. 14.26. Представление объекта регулирования

Если сложный объект представить как n одинаковых инерционных звеньев первого порядка, соединенных последовательно, то его передаточная функция

W ₀ (p) =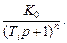

Переходные процессы для такого объекта приведены на рис. 14.27, где K ₀ = 1.

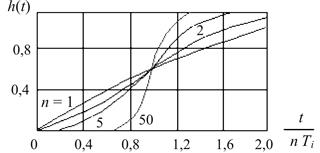
Рис. 14.27. Переходные процессы для n одиночных звеньев

Длительность апериодического переходного процесса можно определить:

t_n > ,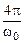

где ω₀ – полоса пропускания[3].

Для малоколебательных переходных процессов

t_n = .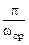

Все новейшие САР используют цифровые регуляторы. Требуется правильно выбрать период квантования. Можно воспользоваться теоремой Котельникова–Шеннона, по которой

f _кв > ω₀ / 2π.

Также рекомендуется выбирать период квантования из соотношения

T ₉₅ / 15 < 1/ f _кв < T ₉₅ / 5,

где T ₉₅ – время достижения выходным сигналом уровня 95 % от установившегося значения при подаче на вход объекта ступенчатого сигнала. Можно принимать T ₉₅ ≈ τ_об + 3 T _об.

Дата добавления: 2015-05-29