
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
LII. Плоскость и прямая в пространстве 1 страница
|
|
|
|
Чтобы составить уравнение прямой в пространстве, следует знать на этой прямой какую-либо точку, которая называется начальной точкой, и направляющий вектор этой прямой.
Основные виды уравнений прямой в пространстве
§3.3. Прямая в пространстве
Определение 3.5. Направляющим вектором прямой называется любой ненулевой вектор, параллельный этой прямой.
Будем использовать следующие обозначения: 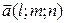 В– направляющий вектор РїСЂСЏРјРѕР№,
В– направляющий вектор РїСЂСЏРјРѕР№, 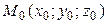 В– начальная (заданная) точка РЅР° РїСЂСЏРјРѕР№,
В– начальная (заданная) точка РЅР° РїСЂСЏРјРѕР№, 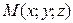 В– произвольная (текущая) точка этой РїСЂСЏРјРѕР№,
В– произвольная (текущая) точка этой РїСЂСЏРјРѕР№, 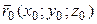 Врадиус-вектор точки
Врадиус-вектор точки 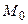 ,
, 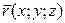 В– радиус-вектор точки
В– радиус-вектор точки  .
.
| Данные | УравненияВВВВВ | Название | |
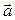 , , 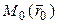
| 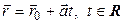
| векторное параметрическое | (3.26) |
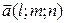 , , 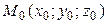
| 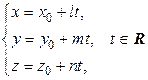
| параметрические | (3.27) |
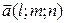 , , 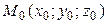
| 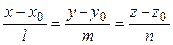
| канонические | (3.28) |
Кроме того, прямую в пространстве можно задать в виде пересечения плоскостей:
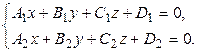
Заметим, что в этих уравнениях коэффициенты при неизвестных не должны быть пропорциональными.
Пример 3.24. Составить канонические уравнения РїСЂСЏРјРѕР№, проходящей через точки  ВРё
ВРё  .
.
∆ В качестве направляющего вектора возьмем 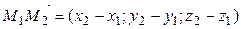 , в качестве начальной точки – точку
, в качестве начальной точки – точку 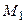 . Канонические уравнения записываем по примеру уравнений (3.28):
. Канонические уравнения записываем по примеру уравнений (3.28): 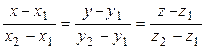 .▲
.в–І
Пример 3.25. Для РїСЂСЏРјРѕР№ 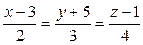 Взаписать уравнения:
Взаписать уравнения:
а) параметрические; б) в виде пересечения плоскостей.
∆ Р°) Прямая задана каноническими уравнениями, РёР· которых находим начальную точку 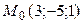 В(ее координаты СЃ противоположными знаками записаны РІ числителях) Рё направляющий вектор
В(ее координаты СЃ противоположными знаками записаны РІ числителях) Рё направляющий вектор 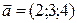 , координаты которого находятся РІ знаменателях. Параметрические уравнения записываем РїРѕ примеру уравнений (3.27):
, координаты которого находятся в знаменателях. Параметрические уравнения записываем по примеру уравнений (3.27): 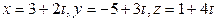 .
.
б) Канонические уравнения прямой – это система трех уравнений первой степени:
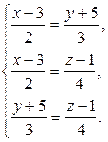
РћРґРЅРѕ РёР· РЅРёС… является следствием РґРІСѓС… РґСЂСѓРіРёС…. Каждое РёР· этих уравнений РІ пространстве задает плоскость. Если точка лежит РЅР° РїСЂСЏРјРѕР№, то РѕРЅР° лежит РІРѕ всех трех плоскостях, С‚.Рµ. ее координаты удовлетворяют всем трем уравнениям. Для однозначного задания РїСЂСЏРјРѕР№ достаточно оставить РґРІР° РёР· РЅРёС…. Например, оставим первое Рё второе. После преобразований получим 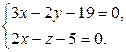 ВКонечно, задача имеет РЅРµ единственное решение, так как через данную РїСЂСЏРјСѓСЋ РІ пространстве РїСЂРѕС…РѕРґРёС‚ бесчисленное множество плоскостей. Для ответа РїРѕРґС…РѕРґСЏС‚ любые РґРІРµ РёР· РЅРёС…. в–І
ВКонечно, задача имеет РЅРµ единственное решение, так как через данную РїСЂСЏРјСѓСЋ РІ пространстве РїСЂРѕС…РѕРґРёС‚ бесчисленное множество плоскостей. Для ответа РїРѕРґС…РѕРґСЏС‚ любые РґРІРµ РёР· РЅРёС…. в–І
Пример 3.26. Для РїСЂСЏРјРѕР№ 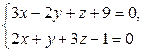 Всоставить параметрические уравнения.
Всоставить параметрические уравнения.
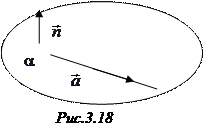
∆ 1-й способ. Для составления параметрических уравнений требуется знать направляющий вектор прямой и какую-нибудь ее точку. Заданная прямая представлена в виде пересечения плоскостей. Если прямая лежит в плоскости 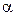 , то ее направляющий вектор
, то ее направляющий вектор 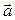 Вперпендикулярен нормальному вектору
Вперпендикулярен нормальному вектору 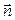 Вэтой плоскости (СЂРёСЃ.3.18). Поэтому направляющий вектор РїСЂСЏРјРѕР№, заданной РІ РІРёРґРµ пересечения плоскостей, перпендикулярен как нормальному вектору
Вэтой плоскости (СЂРёСЃ.3.18). Поэтому направляющий вектор РїСЂСЏРјРѕР№, заданной РІ РІРёРґРµ пересечения плоскостей, перпендикулярен как нормальному вектору 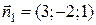 Впервой плоскости, так Рё нормальному вектору
Впервой плоскости, так Рё нормальному вектору 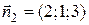 Ввторой. Найдем векторное произведение:
Ввторой. Найдем векторное произведение:
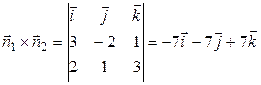 .
.
Направляющим вектором искомой прямой возьмем вектор 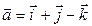 , коллинеарный векторному произведению.
, коллинеарный векторному произведению.
Система, которая задает РїСЂСЏРјСѓСЋ, имеет бесчисленное множество решений. Р’ качестве координат начальной точки можно взять любое РёР· РЅРёС…. Р?РЅРѕРіРґР° это решение можно просто увидеть. Если же увидеть РЅРµ удается, зафиксируем РѕРґРЅРѕ РёР· неизвестных, например, положим 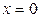 ВРё решим полученную систему (тем самым РјС‹ ищем точку пересечения заданной РїСЂСЏРјРѕР№ СЃ плоскостью
ВРё решим полученную систему (тем самым РјС‹ ищем точку пересечения заданной РїСЂСЏРјРѕР№ СЃ плоскостью  ):
):
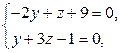 В
В  В
В 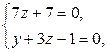 В
В 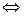 В
В 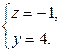
Таким образом, искомая точка – это 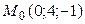 . Записываем параметрические уравнения:
. Записываем параметрические уравнения: 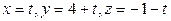 .
.
2-Р№ СЃРїРѕСЃРѕР±. Возьмем РІ качестве параметра РѕРґРЅСѓ РёР· переменных, например, положим 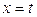 ВРё выразим РёР· системы остальные переменные через
ВРё выразим РёР· системы остальные переменные через 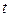 :
:
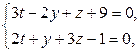 В
В  В
В 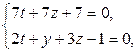 В
В  В
В 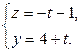
Получили те же уравнения: 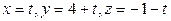 .
.
Очень часто второй способ оказывается проще первого, так как нет необходимости искать векторное произведение, а системы приходится решать в обоих случаях. ▲
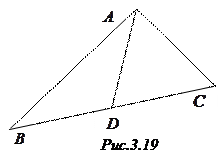
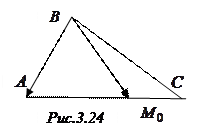
Пример 3.27. Заданы вершины треугольника 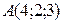 ,
, 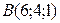 ВРё
ВРё 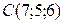 . Составить:
. Составить:
а) векторное параметрическое уравнение медианы, проведенной из вершины 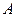 ;
;
б) параметрические уравнения биссектрисы внутреннего угла и биссектрисы внешнего угла при вершине 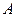 ;
;
в) уравнения высоты, проведенной из вершины 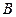 , в виде пересечения плоскостей;
, в виде пересечения плоскостей;
г) канонические уравнения высоты, проведенной из вершины 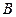 .
.
∆ а) Для составления векторного параметрического уравнения прямой (уравнения типа (3.26)) надо знать ее направляющий вектор и какую-нибудь точку. В качестве начальной точки можно взять 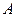 , в качестве направляющего вектора – вектор, коллинеарный
, в качестве направляющего вектора – вектор, коллинеарный 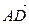 , где
, РіРґРµ 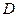 В– середина
В– середина 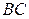 В(СЂРёСЃ. 3.19). Переходим Рє вычислениям:
В(СЂРёСЃ. 3.19). Переходим Рє вычислениям: 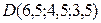 ,
, 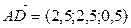 ,
, 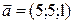 . Векторные параметрические уравнения медианы (т.е. прямой, на которой лежит медиана):
. Векторные параметрические уравнения медианы (т.е. прямой, на которой лежит медиана): 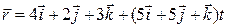 .
.
 б) Для составления параметрических уравнений прямой также требуются начальная точка и направляющий вектор. Начальной точкой может служить все та же точка
Р±) Для составления параметрических уравнений РїСЂСЏРјРѕР№ также требуются начальная точка Рё направляющий вектор. Начальной точкой может служить РІСЃРµ та же точка 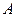 . Р?Р· векторной алгебры РјС‹ знаем, что вектор
. Р?Р· векторной алгебры РјС‹ знаем, что вектор 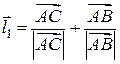 Вделит пополам внутренний СѓРіРѕР», Р° вектор
Вделит пополам внутренний СѓРіРѕР», Р° вектор 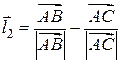 В– внешний СѓРіРѕР» треугольника РїСЂРё вершине
В– внешний СѓРіРѕР» треугольника РїСЂРё вершине 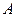 В(СЂРёСЃ.3.20). Переходим Рє вычислениям:
В(СЂРёСЃ.3.20). Переходим Рє вычислениям:
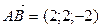 ,
, 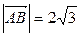 ;
; 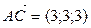 ,
, 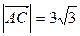 ;
; 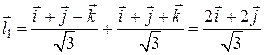 ,
, 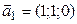
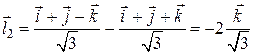 ,
,  .
.
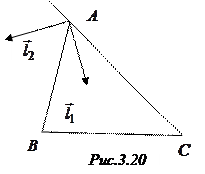 Параметрические уравнения биссектрисы внутреннего угла при вершине
Параметрические уравнения биссектрисы внутреннего угла при вершине 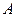 :
: 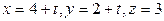 ;
;
параметрические уравнения биссектрисы внешнего угла при вершине 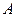 :
: 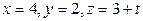 .
.
РІ) Р’ этом случае требуется найти РґРІРµ плоскости, проходящие через РїСЂСЏРјСѓСЋ, РЅР° которой лежит высота треугольника. РћРґРЅРѕР№ РёР· этих плоскостей, очевидно, является плоскость 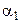 Взаданного треугольника, Р° второй – плоскость
Взаданного треугольника, Р° второй – плоскость 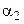 , проходящая через
, проходящая через 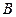 Вперпендикулярно вектору
Вперпендикулярно вектору 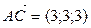 В(СЂРёСЃ.3.21). Для плоскости
В(СЂРёСЃ.3.21). Для плоскости 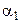 Вимеем РґРІР° вектора, параллельных ей:
Вимеем РґРІР° вектора, параллельных ей: 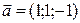 В(
В(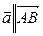 ) Рё
) Рё 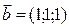 В(
В(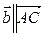 ); для плоскости
); для плоскости 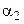 В– вектор
В– вектор 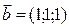 , перпендикулярный
, перпендикулярный 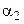 . Составляем общие уравнения плоскостей, выбирая для каждой из них в качестве начальной точку
. Составляем общие уравнения плоскостей, выбирая для каждой из них в качестве начальной точку 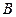 .
.
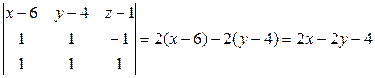 ,
,
значит, 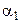 Вимеет уравнение
Вимеет уравнение 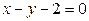 , Р°
, Р° 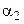 В– уравнение
В– уравнение
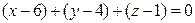 Вили
Вили 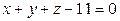 .
.
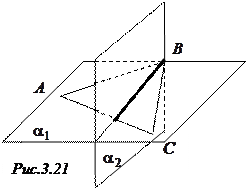 Р?скомая прямая задается системой
Р?скомая прямая задается системой 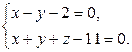
г) Для составления канонических уравнений требуется начальная точка (ею может служить, например, точка 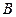 ) и направляющий вектор. Чтобы найти направляющий вектор предлагаются три способа.
) и направляющий вектор. Чтобы найти направляющий вектор предлагаются три способа.
 1-й способ. Направляющий вектор высоты ортогонален вектору
1-Р№ СЃРїРѕСЃРѕР±. Направляющий вектор высоты ортогонален вектору 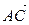 ВРё вектору
ВРё вектору 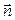 , перпендикулярному плоскости треугольника (СЂРёСЃ.3.22). Р’ СЃРІРѕСЋ очередь, вектор
, перпендикулярному плоскости треугольника (СЂРёСЃ.3.22). Р’ СЃРІРѕСЋ очередь, вектор 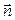 Вортогонален векторам
Вортогонален векторам 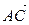 ВРё
ВРё 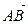 . Вектор, перпендикулярный РґРІСѓРј заданным, можно найти как РёС… векторное произведение. Поэтому
. Вектор, перпендикулярный двум заданным, можно найти как их векторное произведение. Поэтому
ВВВВВВВВВВВВВВВВ 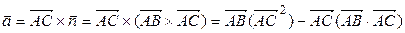 . ВВВВВВВВВВВ(3.29)
. ВВВВВВВВВВВ(3.29)
Подставляя координаты векторов 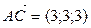 ВРё
ВРё 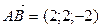 , получаем
, получаем
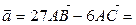
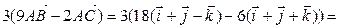
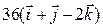 .
.
2-Р№ СЃРїРѕСЃРѕР±. Если  В– высота треугольника
В– высота треугольника  , то РїРѕ СЂРёСЃСѓРЅРєСѓ 3.23 РІРёРґРёРј, что
, то по рисунку 3.23 видим, что
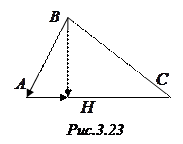
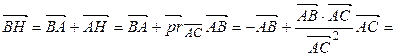
ВВВ ВВВВВ 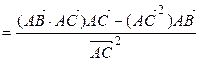 .ВВВВВ ВВВВВВВВВВВВВВВВВВВ(3.30)
.ВВВВВ ВВВВВВВВВВВВВВВВВВВ(3.30)
Сравнивая (3.29) и (3.30), замечаем, что векторы, найденные двумя способами, получились, как и следовало ожидать, коллинеарными.
3-й способ. Запишем параметрические уравнения прямой  :
: 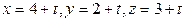 . Если
. Если 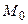 В– некоторая точка этой РїСЂСЏРјРѕР№, то ее координаты получаются РёР· параметрических уравнений РїСЂРё некотором значении
В– некоторая точка этой РїСЂСЏРјРѕР№, то ее координаты получаются РёР· параметрических уравнений РїСЂРё некотором значении 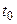 , С‚.Рµ.
, С‚.Рµ. 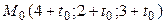 . РўРѕРіРґР°
. РўРѕРіРґР° 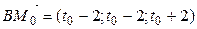 В(СЂРёСЃ.3.24). Чтобы
В(СЂРёСЃ.3.24). Чтобы 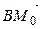 Вбыл ортогонален вектору
Вбыл ортогонален вектору 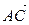 , потребуем, чтобы РёС… скалярное произведение равнялось нулю:
, потребуем, чтобы РёС… скалярное произведение равнялось нулю: 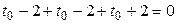 В
В 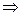 В
 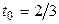 . Таким образом,
. Таким образом, 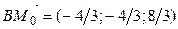 , и опять получили вектор, коллинеарный двум предыдущим.
, и опять получили вектор, коллинеарный двум предыдущим.
 Записываем канонические уравнения высоты, используя в качестве начальной точку
Записываем канонические уравнения высоты, используя в качестве начальной точку 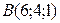 , а в качестве направляющего вектора –
, а в качестве направляющего вектора – 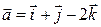 :
: 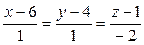 .в–І
.в–І
Взаимное расположение прямых в пространстве можно выяснить двумя способами.
 1-й способ. Какими бы уравнениями ни была задана прямая в пространстве, всегда можно найти ее направляющий вектор и какую-либо точку на этой прямой. Предположим, что в пространстве заданы две прямые
1-Р№ СЃРїРѕСЃРѕР±. Какими Р±С‹ уравнениями РЅРё была задана прямая РІ пространстве, всегда можно найти ее направляющий вектор Рё какую-либо точку РЅР° этой РїСЂСЏРјРѕР№. Предположим, что РІ пространстве заданы РґРІРµ прямые 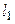 ВРё
ВРё 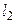 . Обозначим РёС… направляющие векторы соответственно
. Обозначим РёС… направляющие векторы соответственно  ВРё
ВРё 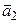 . Выберем также РЅР° каждой РёР· этих прямых РїРѕ точке:
. Выберем также на каждой из этих прямых по точке: 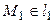 ,
, 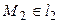 .
.
 Два вектора либо коллинеарны, либо неколлинеарны. Если векторы
Два вектора либо коллинеарны, либо неколлинеарны. Если векторы  ВРё
ВРё  Вколлинеарны, то прямые РјРѕРіСѓС‚ либо быть параллельными, либо совпадать. Р’ том случае, РєРѕРіРґР° прямые совпадают, точки
Вколлинеарны, то прямые РјРѕРіСѓС‚ либо быть параллельными, либо совпадать. Р’ том случае, РєРѕРіРґР° прямые совпадают, точки  ВРё
ВРё  В– это РґРІРµ точки РЅР° РѕРґРЅРѕР№ Рё той же РїСЂСЏРјРѕР№, поэтому вектор
В– это РґРІРµ точки РЅР° РѕРґРЅРѕР№ Рё той же РїСЂСЏРјРѕР№, поэтому вектор 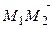 Вколлинеарен каждому РёР· векторов
Вколлинеарен каждому РёР· векторов  ВРё
ВРё 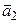 В(СЂРёСЃ. 3.25). Если прямые параллельны, то вектор
В(СЂРёСЃ. 3.25). Если прямые параллельны, то вектор 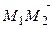 Внаправляющим векторам
Внаправляющим векторам  ВРё
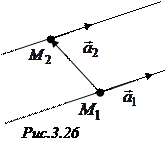
ВРё 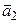 Внеколлинеарен (СЂРёСЃ. 3.26).
Внеколлинеарен (СЂРёСЃ. 3.26).
Если же векторы  ВРё
ВРё 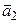 Внеколлинеарны, то прямые либо пересекаются, либо скрещиваются. Скрещивающимися называются те прямые, через которые нельзя провести РѕРґРЅСѓ плоскость. Поэтому, если векторы
Внеколлинеарны, то прямые либо пересекаются, либо скрещиваются. Скрещивающимися называются те прямые, через которые нельзя провести РѕРґРЅСѓ плоскость. Поэтому, если векторы  ,
, 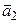 ВРё
ВРё 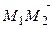 Внекомпланарны, то прямые скрещиваются, РІ противном случае РѕРЅРё пересекаются.
Внекомпланарны, то прямые скрещиваются, РІ противном случае РѕРЅРё пересекаются.
Вывод:
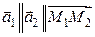 В– прямые совпадают;
В– прямые совпадают;
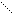
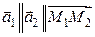 В– прямые параллельны;
В– прямые параллельны;
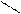
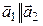 ,
,  ,
, 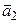 ВРё
ВРё 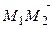 Вкомпланарны – прямые пересекаются;
Вкомпланарны – прямые пересекаются;
 ,
, 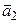 ВРё
ВРё 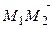 Внекомпланарны – прямые скрещиваются.
Внекомпланарны – прямые скрещиваются.
2-Р№ СЃРїРѕСЃРѕР±.  Взаимное Врасположение Впрямых ВРІ Впространстве Втакже
почти всегда можно распознать по количеству их общих точек: если две прямые имеют одну общую точку, то они пересекаются, если бесчисленное множество – то совпадают, и только тогда, когда прямые общих точек не имеют, требуется дополнительное исследование (например, по взаимному расположению направляющих векторов).
Пример 3.28. Выяснить взаимное расположение пар прямых:
ВВВВ Р°) 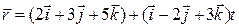 ВВРёВ
ВВРёВ  ;
;
ВВВВ Р±) 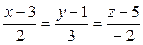 ВВРёВ
ВВРёВ 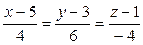 ;
;
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 504; Нарушение авторских прав?; Мы поможем в написании вашей работы!