
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
LII. Плоскость и прямая в пространстве 2 страница
|
|
|
|
ВВВВ РІ) 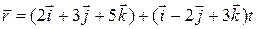 ВВРёВ
ВВРёВ 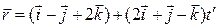 .
.
∆ Так как во всех трех случаях известны начальные точки прямых и их направляющие векторы, то более рациональным будет первый способ.
Р°) Координаты направляющих векторов 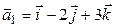 ВРё
ВРё 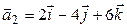 Впропорциональны, поэтому РѕРЅРё коллинеарны. Р?Р· уравнений прямых также находим
Впропорциональны, поэтому РѕРЅРё коллинеарны. Р?Р· уравнений прямых также находим 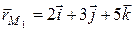 ,
, 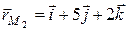 , значит,
, значит,
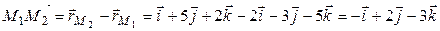 .
.
Так как 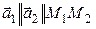 , то прямые совпадают.
, то прямые совпадают.
б) направляющие векторы 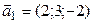 ,
, 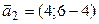 Вопять коллинеарны, прямые либо параллельны, либо совпадают. Рти РґРІР° случая можно различить Рё так: РІ случае совпадения каждая точка РѕРґРЅРѕР№ РёР· прямых принадлежит также Рё второй. Р?Р· уравнений первой РїСЂСЏРјРѕР№ находим РѕРґРЅСѓ РёР· ее точек
Вопять коллинеарны, прямые либо параллельны, либо совпадают. Рти РґРІР° случая можно различить Рё так: РІ случае совпадения каждая точка РѕРґРЅРѕР№ РёР· прямых принадлежит также Рё второй. Р?Р· уравнений первой РїСЂСЏРјРѕР№ находим РѕРґРЅСѓ РёР· ее точек 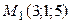 ВРё подставляем ее координаты РІ уравнения второй РїСЂСЏРјРѕР№:
ВРё подставляем ее координаты РІ уравнения второй РїСЂСЏРјРѕР№: 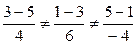 . Таким образом,
. Таким образом, 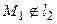 , поэтому прямые параллельны.
, поэтому прямые параллельны.
Замечание. При наличии опыта можно все эти векторы не выписывать, а проверять их коллинеарность, сравнивая коэффициенты непосредственно в уравнениях прямых.
РІ) Р?Р· уравнений прямых находим следующие данные:
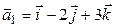 ,
, 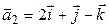 ,
, 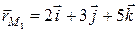 ,
, 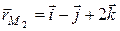 ,
, 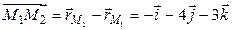 . Проверим компланарность векторов
. Проверим компланарность векторов  ,
, 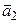 ВРё
ВРё 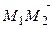 , для чего вычислим РёС… смешанное произведение:
, для чего вычислим их смешанное произведение:

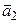
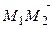 В=
В= 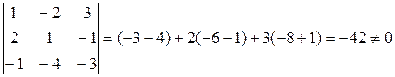 .
.
Так как  ,
, 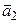 ВРё
ВРё 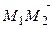 Внекомпланарны, то прямые скрещиваются. в–І
Внекомпланарны, то прямые скрещиваются. в–І
Пример 3.29. Выяснить взаимное расположение прямых. В случае их пересечения найти точку пересечения.
ВВВВ Р°)  ВВРёВ
ВВРёВ 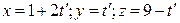 ;
;
ВВВВ Р±) 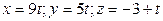 ВРёВ
ВРёВ 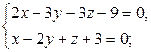
ВВВВ РІ) 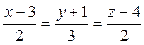 ВРё
ВРё 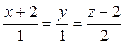 ;
;
ВВВВ Рі) 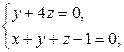
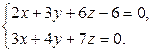
∆ Рту задачу лучше решать вторым СЃРїРѕСЃРѕР±РѕРј, С‚.Рє. точку пересечения РІСЃРµ равно искать придется.
а) Чтобы найти общие точки прямых, надо решить систему, состоящую из всех уравнений, задающих обе прямые. Таким образом, получаем систему из шести уравнений. Для решения же конкретной системы, полученной в этой задаче, проще всего приравнять неизвестные 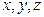 , выраженные в уравнениях каждой из прямых через
, выраженные РІ уравнениях каждой РёР· прямых через 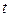 ВРё
ВРё 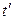 Всоответственно:
Всоответственно:
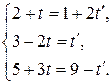
Получили систему трех уравнений СЃ РґРІСѓРјСЏ неизвестными. Р?Р· РґРІСѓС… последних уравнений находим 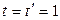 . Рти значения удовлетворяют Рё первому уравнению, РІ чем можно убедиться непосредственной подстановкой. Система имеет единственное решение, значит, прямые пересекаются. Чтобы найти точку пересечения, следует полученное значение
. Рти значения удовлетворяют Рё первому уравнению, РІ чем можно убедиться непосредственной подстановкой. Система имеет единственное решение, значит, прямые пересекаются. Чтобы найти точку пересечения, следует полученное значение 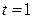 Вподставить РІ уравнения первой РїСЂСЏРјРѕР№, либо
Вподставить РІ уравнения первой РїСЂСЏРјРѕР№, либо 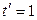 В– РІ уравнения второй. Таким образом, точкой пересечения является
В– РІ уравнения второй. Таким образом, точкой пересечения является 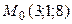 .
.
ВВВВ Р±) решаем систему, состоящую РёР· уравнений, задающих РѕР±Рµ прямые:

Решать же эту систему проще всего так: неизвестные 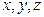 , выраженные РІ первых трех уравнениях через
, выраженные в первых трех уравнениях через 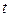 , подставим в два последних, в результате чего получим систему двух уравнений с одним неизвестным:
, подставим в два последних, в результате чего получим систему двух уравнений с одним неизвестным:
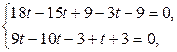 В
В  В
В 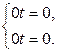
Система имеет бесчисленное множество решений, поэтому прямые совпадают.
 в) Перепишем уравнения первой прямой в параметрическом виде, а второй – в виде пересечения плоскостей:
в) Перепишем уравнения первой прямой в параметрическом виде, а второй – в виде пересечения плоскостей: 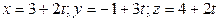 ;
; 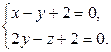 ВПоступая, как РїСЂРё решении предыдущей задачи, получаем систему:
ВПоступая, как РїСЂРё решении предыдущей задачи, получаем систему:
ВВВ 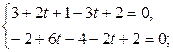 В
В 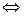 В
В 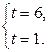 ВВВВВВВВВВВВВВВ(3.31)
ВВВВВВВВВВВВВВВ(3.31)
 Р’ этом случае РѕРЅР° РЅРµ имеет решений, значит, прямые либо параллельны, либо скрещиваются. Проанализируем метод решения задачи. Вторая прямая задана РІ РІРёРґРµ пересечения плоскостей. Решая каждое РёР· уравнений системы (3.31), замечаем, что первая прямая пересекает каждую РёР· этих плоскостей, РЅРѕ РІ разных точках, откуда делаем вывод, что СЃ линией пересечения РѕРЅР° скрещивается (СЂРёСЃ.3.27).
Р’ этом случае РѕРЅР° РЅРµ имеет решений, значит, прямые либо параллельны, либо скрещиваются. Проанализируем метод решения задачи. Вторая прямая задана РІ РІРёРґРµ пересечения плоскостей. Решая каждое РёР· уравнений системы (3.31), замечаем, что первая прямая пересекает каждую РёР· этих плоскостей, РЅРѕ РІ разных точках, откуда делаем вывод, что СЃ линией пересечения РѕРЅР° скрещивается (СЂРёСЃ.3.27).
 Вообще, в том случае, когда одна из прямых задана параметрическими уравнениями, а вторая – в виде пересечения плоскостей, используя описанный метод решения, получаем систему двух линейных уравнений с одним неизвестным (систему типа (3.31)). Так как каждое из линейных уравнений с одним неизвестным может либо иметь единственное решение, либо бесчисленное множество решений, либо не иметь решений вовсе, то кроме описанных двух случаев могут возникать еще и следующие:
Вообще, в том случае, когда одна из прямых задана параметрическими уравнениями, а вторая – в виде пересечения плоскостей, используя описанный метод решения, получаем систему двух линейных уравнений с одним неизвестным (систему типа (3.31)). Так как каждое из линейных уравнений с одним неизвестным может либо иметь единственное решение, либо бесчисленное множество решений, либо не иметь решений вовсе, то кроме описанных двух случаев могут возникать еще и следующие:
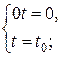 Всистема имеет единственное решение, прямые пересекаются;
Всистема имеет единственное решение, прямые пересекаются;
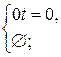 Впервая прямая принадлежит первой плоскости, Р° второй параллельна, РїРѕ отношению Рє линии пересечения параллельна (СЂРёСЃ.3.28);
Впервая прямая принадлежит первой плоскости, Р° второй параллельна, РїРѕ отношению Рє линии пересечения параллельна (СЂРёСЃ.3.28);
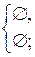 Впервая Впрямая параллельна каждой ВРёР· Впересекающихся плоско-
Впервая Впрямая параллельна каждой ВРёР· Впересекающихся плоско-
стей, по отношению к линии пересечения параллельна (рис.3.29);
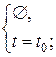 Впервая прямая параллельна первой плоскости, Р° вторую пересекает, СЃ линией пересечения скрещивается (СЂРёСЃ.3.30).
Впервая прямая параллельна первой плоскости, Р° вторую пересекает, СЃ линией пересечения скрещивается (СЂРёСЃ.3.30).
 ВВВВ Рі) Перепишем уравнения первой РїСЂСЏРјРѕР№ РІ параметрическом РІРёРґРµ. Р’ качестве параметра выберем, например, переменную
ВВВВ Рі) Перепишем уравнения первой РїСЂСЏРјРѕР№ РІ параметрическом РІРёРґРµ. Р’ качестве параметра выберем, например, переменную 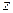 В
 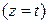 . Тогда из первого уравнения прямой получаем
. Тогда из первого уравнения прямой получаем 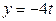 , а из второго –
, а из второго – 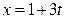 , и в результате параметрические уравнения первой прямой выглядят так:
, и в результате параметрические уравнения первой прямой выглядят так: 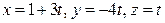 . Составляем и решаем систему из уравнений обеих прямых:
. Составляем и решаем систему из уравнений обеих прямых:
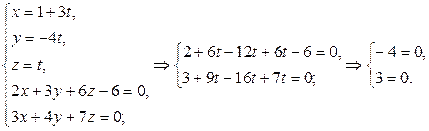
Р?Р· последней системы РІРёРґРёРј, что первая прямая параллельна каждой РёР· плоскостей, задающих вторую РїСЂСЏРјСѓСЋ (СЂРёСЃ. 3.29). Рто означает, что заданные прямые параллельны. в–І
Вывод. Если прямые 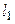 ВРё
ВРё 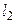 заданы параметрическими или каноническими уравнениями, то взаимное расположение РёС… направляющих векторов определяется непосредственно РёР· уравнений. Р’ том случае, РєРѕРіРґР° векторы коллинеарны, прямые параллельны или совпадают, остается проверить, принадлежит ли РїСЂСЏРјРѕР№
заданы параметрическими или каноническими уравнениями, то взаимное расположение РёС… направляющих векторов определяется непосредственно РёР· уравнений. Р’ том случае, РєРѕРіРґР° векторы коллинеарны, прямые параллельны или совпадают, остается проверить, принадлежит ли РїСЂСЏРјРѕР№ 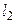 Вкакая-либо точка РїСЂСЏРјРѕР№
Вкакая-либо точка РїСЂСЏРјРѕР№ 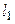 . Р’Рѕ всех остальных случаях лучше искать общие точки (2-Р№ СЃРїРѕСЃРѕР±), причем система для РёС… нахождения проще всего решается, РєРѕРіРґР° РѕРґРЅР° РёР· прямых задана параметрическими уравнениями, Р° вторая – РІ РІРёРґРµ пересечения плоскостей. Если это РЅРµ так, имеет смысл перейти именно Рє этим способам задания (СЃРј. пример 3.29).
. Во всех остальных случаях лучше искать общие точки (2-й способ), причем система для их нахождения проще всего решается, когда одна из прямых задана параметрическими уравнениями, а вторая – в виде пересечения плоскостей. Если это не так, имеет смысл перейти именно к этим способам задания (см. пример 3.29).
28. Уравнения плоскости, проходящей через
а)данную точку параллельно двум неколлинеарным векторам;
Дано: R = 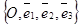 , М0(х0, у0, z0),
, М0(х0, у0, z0), 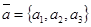 ,
, 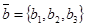 ,
, 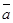 и
и 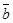 неколлинеарны; П ' М0, П //
неколлинеарны; П ' М0, П // 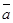 , П //
, П // 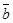 .
.
Найти условия, определяющие П (рис. 46).
Решение. М Î П Û  ,
, 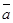 и
и 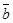 компланарны. Так как
компланарны. Так как 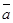 и
и 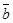 неколлинеарны, то М Î П Û либо
неколлинеарны, то М Î П Û либо 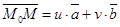 (u,v - любые действительные числа), либо определитель, составленный из координат этих векторов, равен нулю. Перепишем эти условия в координатах. Получим М Î П Û
(u,v - любые действительные числа), либо определитель, составленный из координат этих векторов, равен нулю. Перепишем эти условия в координатах. Получим М Î П Û 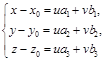 или М Î П Û
или М Î П Û 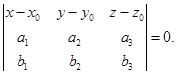 (39)
(39)
Получили два вида уравнений плоскости: уравнение (39) и 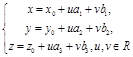 (40).
(40).
Уравнения (40) называются параметрическими уравнениями плоскости, проходящей через данную точку параллельно двум данным векторам.
Так как 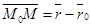 , где
, где 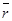 и
и 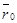 - радиусы-векторы точек М и М0 соответственно. Тогда уравнение
- радиусы-векторы точек М и М0 соответственно. Тогда уравнение 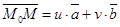 можно переписать
можно переписать 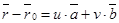 (41). Это векторное уравнение плоскости.
(41). Это векторное уравнение плоскости.
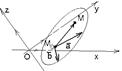

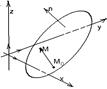
Рис. 46 Рис. 47 Рис. 48
б)три не лежащие на одной прямой точки;
Дано: R =  , М1(х1, у1,z1), М2(х2, у2, z2), М3(x3, у3, z3), точки M1, M2, M3 не коллинеарные. П É í M1, M2, M3ý.
, М1(х1, у1,z1), М2(х2, у2, z2), М3(x3, у3, z3), точки M1, M2, M3 не коллинеарные. П É í M1, M2, M3ý.
Найти уравнения П (рис. 47).
Решение. Так как M1, M2, M3 не коллинеарные, то векторы
 и
и 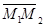 неколлинеарны. Используя уравнение (41), получим векторное уравнение плоскости, проходящей через три данные точки:
неколлинеарны. Используя уравнение (41), получим векторное уравнение плоскости, проходящей через три данные точки:
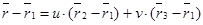 . (42)
. (42)
Используя (40) и (39), получим параметрические уравнения плоскости П и её уравнение в форме определителя. 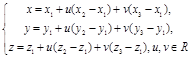 (43);
(43); 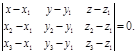 (44)
(44)
в)данную точку перпендикулярно данному вектору.
Дано: 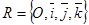 , М 0(х0, у0, z0),
, М 0(х0, у0, z0), 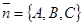 ,
, 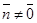 , П ' М0, П ^
, П ' М0, П ^ 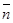 .
.
Найти уравнение П.
Решение. М Î П Û либо 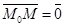 , либо
, либо 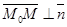 Û
Û 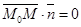 . Так как
. Так как 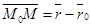 , то М Î П Û
, то М Î П Û 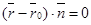 (47)Это векторное уравнение данной плоскости.
(47)Это векторное уравнение данной плоскости.
Переходя к координатам, получим А (х - х0) + В (у - у0) + С(z - z0) = 0(48)
Можно показать, что если плоскость задана в ПДСК общим уравнением (45), то вектор 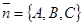 перпендикулярен этой плоскости.
перпендикулярен этой плоскости.
29. Общее уравнение плоскости.
Если в уравнениях (39) или (44) раскрыть определители, то получим уравнение первой степени с тремя переменными, следовательно, в аффинной системе координат всякая плоскость может быть задана некоторым уравнением вида Ах + Ву + Сz + D = 0. Поставим обратную задачу: всякое ли уравнение вида Ах + Ву + Сz + D = 0 задаёт в аффинной системе координат некоторую плоскость.
Дано: R = 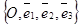 , Ах + Ву + Сz + D = 0 (45), где коэффициенты А, В, С не все равны нулю.
, Ах + Ву + Сz + D = 0 (45), где коэффициенты А, В, С не все равны нулю.
Доказать: уравнение (45) задаёт плоскость.
Доказательство. Проведём доказательство, предполагая, что А ¹ 0. Если y = z = 0, то 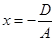 . Следовательно, координаты точки М0 (
. Следовательно, координаты точки М0 (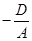 , 0, 0) удовлетворяют уравнению (45), т.е. если плоскость существует, то она обязательно пройдёт через эту точку. Векторы
, 0, 0) удовлетворяют уравнению (45), т.е. если плоскость существует, то она обязательно пройдёт через эту точку. Векторы 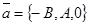 и
и 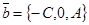 , очевидно, не коллинеарны. Используя (39), составим уравнение плоскости, проходящей через точку М0 параллельно векторам
, очевидно, не коллинеарны. Используя (39), составим уравнение плоскости, проходящей через точку М0 параллельно векторам 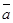 и
и 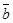 . Получим
. Получим 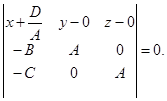
После упрощения: Ах + Ву + Сz + D = 0, т.е. данное уравнение. Итак, (45) действительно задаёт плоскость.
Уравнение (45) называется общее уравнение плоскости.
Следствие. Если плоскость задана общим уравнением (45), то из векторов 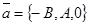 ,
, 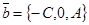 и
и 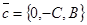 хотя бы два отличны от
хотя бы два отличны от 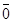 и неколлинеарны. Любой ненулевой вектор из них параллелен данной плоскости.
и неколлинеарны. Любой ненулевой вектор из них параллелен данной плоскости.
30. Нормальное уравнение плоскости. Приведение общего уравнения плоскости к нормальному виду.
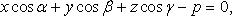 где
где 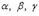 - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.
- углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.
Приведение общего уравнения плоскости к нормальному виду:
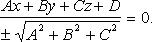 Здесь
Здесь 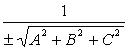 - нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если
- нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если 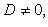 произвольно, если D = 0.
произвольно, если D = 0.
31. Исследование взаимного расположения двух и трёх плоскостей.
Дано: R = 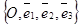 , П1: А1х + В1у + С1z + D1 = 0, П2: А2х + В2у + С2z + D2 = 0.
, П1: А1х + В1у + С1z + D1 = 0, П2: А2х + В2у + С2z + D2 = 0.
Исследовать взаимное расположение П1, П2.
Решение. Задача сводится к исследованию системы 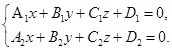 (46)
(46)
Возможны случаи.
1.А1,В1,С1 и А2, В2, С2 не пропорциональны. В этом случае система (46) имеет бесконечно много решений, но уравнения не пропорциональны. На геометрическом языке получаем, что плоскости имеют бесконечно много общих точек, но не совпадают. Следовательно, П1 и П2 пересекаются по прямой.
Замечание. Если прямая задана общими уравнениями (19), то каждое отдельно взятое уравнение задаёт прямую, т.е. прямая задаётся как линия пересечения двух плоскостей.
2. 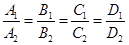 . В этом случае уравнения системы (46) эквивалентны, т.е. каждое решение одного из них является решением второго. На геометрическом языке: каждая точка одной плоскости лежит на другой, т.е. плоскости совпадают.
. В этом случае уравнения системы (46) эквивалентны, т.е. каждое решение одного из них является решением второго. На геометрическом языке: каждая точка одной плоскости лежит на другой, т.е. плоскости совпадают.
3. 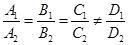 . В этом случае системы (46) не имеет решений. На геометрическом языке: плоскости не имеют общих точек.
. В этом случае системы (46) не имеет решений. На геометрическом языке: плоскости не имеют общих точек.
Следствие. Плоскости П1: А1х + В1у + С1z + D1 = 0, П2: А2х + В2у + С2z + D2 = 0 параллельны тогда и только тогда, когда 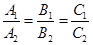 .
.
Задача 16. Исследовать взаимное расположение плоскостей, если одна из них задании общим уравнением, а вторая – параметрическими уравнениями.
Дано: R = 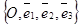 , П1: Ах + Ву + Сz + D = 0, П2:
, П1: Ах + Ву + Сz + D = 0, П2: 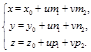 Исследовать взаимное расположение П1, П2.
Исследовать взаимное расположение П1, П2.
Решение. Задача сводится к исследованию системы 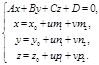 (*)
(*)
Подставив выражения х, у, z в первое уравнение и преобразовав его, получим
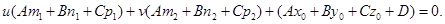 (**)
(**)
Возможны случаи:
1) 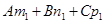 ¹ 0 (или
¹ 0 (или 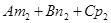 ¹ 0). В этом случае уравнение (**) имеет бесконечно много решений, зависящих от одного параметра. Следовательно, система (*) тоже имеет бесконечно много решений, зависящих от одного параметра. На геометрическом языке это значит, что плоскости пересекаются по прямой.
¹ 0). В этом случае уравнение (**) имеет бесконечно много решений, зависящих от одного параметра. Следовательно, система (*) тоже имеет бесконечно много решений, зависящих от одного параметра. На геометрическом языке это значит, что плоскости пересекаются по прямой.
2) 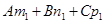 = 0,
= 0, 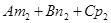 = 0,
= 0, 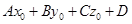 = 0. В этом случае уравнение (**) имеет вид 0×u + 0×v + 0 = 0. Этому уравнению удовлетворяют все возможные значения u и v. На геометрическом языке это значит, что все точки первой плоскости лежат на второй и наоборот. Следовательно, плоскости совпадают.
= 0. В этом случае уравнение (**) имеет вид 0×u + 0×v + 0 = 0. Этому уравнению удовлетворяют все возможные значения u и v. На геометрическом языке это значит, что все точки первой плоскости лежат на второй и наоборот. Следовательно, плоскости совпадают.
3) 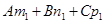 = 0,
= 0, 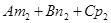 = 0,
= 0, 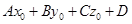 ¹ 0. В этом случае уравнение (**) имеет вид 0×u + 0×v + (
¹ 0. В этом случае уравнение (**) имеет вид 0×u + 0×v + (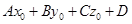 ) = 0. Это уравнение не имеет ни одного решения. На геометрическом языке это значит, что данные плоскости не имеют общих точек.
) = 0. Это уравнение не имеет ни одного решения. На геометрическом языке это значит, что данные плоскости не имеют общих точек.
Следствие. Если П1: Ах + Ву + Сz + D = 0, П2: 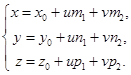 то П1 || П2 Û
то П1 || П2 Û 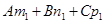 = 0,
= 0, 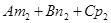 = 0.
= 0.
32. Угол между двумя плоскостями. Условия перпендикулярности двух плоскостей.
Дано: 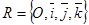 , П1: А1х + В1у + С1z + D1 = 0, П2: А2х + В2у + С2z + D2 = 0.
, П1: А1х + В1у + С1z + D1 = 0, П2: А2х + В2у + С2z + D2 = 0.
Найти один из углов между П1 и П2.
Решение. Из уравнений П1 и П2 следует, что 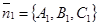 и
и 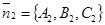 перпендикулярны плоскостям П1 и П2 соответственно. Если О – точка на линии пересечения П1 и П2, t1 и t2 лежат в плоскостях П1 и П2, проходят через точку О и перпендикулярны линии пересечения этих плоскостей (рис. 34), то
перпендикулярны плоскостям П1 и П2 соответственно. Если О – точка на линии пересечения П1 и П2, t1 и t2 лежат в плоскостях П1 и П2, проходят через точку О и перпендикулярны линии пересечения этих плоскостей (рис. 34), то 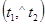 = (П1,
= (П1, 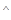 П2). Но по свойству углов со взаимно перпендикулярными сторонами
П2). Но по свойству углов со взаимно перпендикулярными сторонами 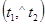 либо равен углу
либо равен углу 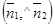 , либо дополняет его до 1800. И в том, и в другом случае
, либо дополняет его до 1800. И в том, и в другом случае 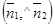 равен одному из углов между П1 и П2. Следовательно,
равен одному из углов между П1 и П2. Следовательно,
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 590; Нарушение авторских прав?; Мы поможем в написании вашей работы!