
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
LII. Плоскость и прямая в пространстве 3 страница
|
|
|
|
Cos((П1,  П2) =
П2) =  (49)
(49)
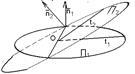


Рис. 49 Рис. 51
Условие перпендикулярности двух плоскостей
Плоскости α и β перпендикулярны, если одна плоскость проходит через перпендикуляр другой плоскости.
 или
или 
33. Расстояние от точки до плоскости.
Дано: 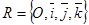 , П: Ах + Ву + Сz + D = 0, М (х0, у0, z0).
, П: Ах + Ву + Сz + D = 0, М (х0, у0, z0).
Найти расстояние d (M0, П) от точки М0 до плоскости П.
Из уравнения плоскости П следует, что вектор 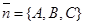 перпендикулярен плоскости П. Опустим из точки М0 перпендикуляр NM0 на плоскость П (рис. 51). Пусть N (x1, y1, z1). Тогда Ax1 + By1 + Cz1 + D = 0 (*). Искомое расстояние d (M0, П) =
перпендикулярен плоскости П. Опустим из точки М0 перпендикуляр NM0 на плоскость П (рис. 51). Пусть N (x1, y1, z1). Тогда Ax1 + By1 + Cz1 + D = 0 (*). Искомое расстояние d (M0, П) = 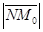 (**)
(**)
Вектор  коллинеарен с вектором
коллинеарен с вектором 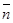 . Так как
. Так как 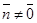 , то
, то  (***). Отсюда и из равенства (**) следует, что d (M0, П) =
(***). Отсюда и из равенства (**) следует, что d (M0, П) =  =
=  (****). Итак, задача свелась к нахождению d. Умножим скалярно на
(****). Итак, задача свелась к нахождению d. Умножим скалярно на 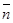 обе части равенства (***), получим
обе части равенства (***), получим 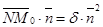 .
.
Перейдя к координатам и учитывая, что система координат прямоугольная, получим A (x0 - x1) + B (y0 - y1) + C (z0 - z1) = d(A2 + B2 + C2). Так как A2 + B2 + C2 ¹ 0, то
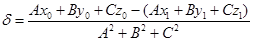 .
.
Из равенства (*) следует, что  = - D. Итак,
= - D. Итак,  . Подставив d в (**), получим d (M0, П) =
. Подставив d в (**), получим d (M0, П) = 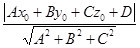 (52)
(52)
Задача 18. Дано: 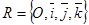 , П: 12 х + 3 у - 4z - 35 = 0.
, П: 12 х + 3 у - 4z - 35 = 0.
Найдите уравнения плоскостей, параллельных П и отстоящих от неё на расстоянии 5.
Решение. Обозначим искомые плоскости П1 и П2. Тогда М Î (П1 È П2) Û d (M, П) = 5. Используя формулу (52), получим М Î (П1 È П2) Û 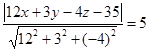 . После упрощения получим
. После упрощения получим 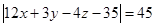 . Раскрывая модуль, получим уравнения двух плоскостей:
. Раскрывая модуль, получим уравнения двух плоскостей:
П1: 12 х + 3 у - 4z - 80 = 0 и П2: 12 х + 3 у - 4z + 10 = 0.
34. Уравнения прямой, проходящей через а) данную точку параллельно данному вектору; б) две данные точки.
а) данную точку параллельно данному вектору (каноническое уравнение прямой)
Пусть прямая проходит через точку 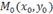 параллельно вектору
параллельно вектору  . Тогда вектор
. Тогда вектор 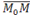 , где
, где 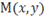 – произвольная точка прямой, коллинеарен вектору
– произвольная точка прямой, коллинеарен вектору 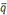 – направляющему вектору прямой
– направляющему вектору прямой 
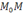 и координаты любой точки прямой
и координаты любой точки прямой 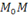 удовлетворяют каноническому уравнению прямой
удовлетворяют каноническому уравнению прямой
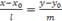 .
.
Уравнение прямой, проходящей через две точки
Если прямая проходит через точки  и
и 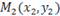 , то ее направляющим вектором можно считать вектор
, то ее направляющим вектором можно считать вектор  .
.
Уравнением прямой, проходящей через две точки  и
и  называется уравнение вида
называется уравнение вида
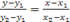 .
.
В случае, когда один из знаменателей равен нулю (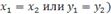 соответствующий числитель тоже равен нулю (
соответствующий числитель тоже равен нулю (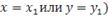 : если
: если 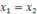 , то прямая, проходящая через точки
, то прямая, проходящая через точки 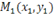 и
и 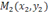 , параллельна оси ординат и ее уравнение имеет вид
, параллельна оси ординат и ее уравнение имеет вид 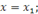
если 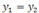 , то прямая, проходящая через точки
, то прямая, проходящая через точки  и
и 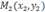 , параллельна оси абсцисс и ее уравнение имеет вид
, параллельна оси абсцисс и ее уравнение имеет вид 
Угловой коэффициент прямой, проходящей через две точки, находится по формуле  .
.
Пример. Составить уравнение прямой, проходящей через точки  и
и 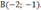
Решение.  или
или 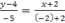 , так как
, так как  , то прямая имеет уравнение
, то прямая имеет уравнение  , значит она параллельная оси ординат.
, значит она параллельная оси ординат.
35. Общие уравнения прямой, приведение общих уравнений к каноническому виду.
Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:
1)найти любое решение  системы
системы

определяя тем самым координаты точки  , принадлежащей прямой;
, принадлежащей прямой;
2) найти направляющий вектор 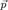 прямой как векторное произведение нормалей
прямой как векторное произведение нормалей 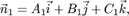
 заданных плоскостей:
заданных плоскостей: 
3) записать каноническое уравнение  с учетом пунктов 1 и 2.
с учетом пунктов 1 и 2.
4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы  и привести подобные члены.
и привести подобные члены.
5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):

6. Если в каноническом уравнении (4.34) прямой фиксировать координаты  точки
точки  , а коэффициентам
, а коэффициентам 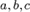 придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке
придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке  , т.е. совокупность всех прямых, проходящих через точку
, т.е. совокупность всех прямых, проходящих через точку  .
.
7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.
36. Исследование взаимного расположения а) двух прямых, б) прямой и плоскости.
Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.
· Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые.
· Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются.
· В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны).
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются.
На рис. 26 прямая a лежит в плоскости  , а прямая с пересекает
, а прямая с пересекает 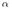 в точке N. Прямые a и с — скрещивающиеся.
в точке N. Прямые a и с — скрещивающиеся.
Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.
 На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость
На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость 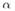 || b (в плоскости
|| b (в плоскости  указана прямая a1 || b).
указана прямая a1 || b).
Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты.
б) прямой и плоскости.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.
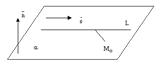


Теорема. Пусть плоскость 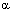 задана общим уравнением
задана общим уравнением 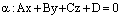 ,а прямая L задана каноническими уравнениями или параметрическими уравнениями
,а прямая L задана каноническими уравнениями или параметрическими уравнениями

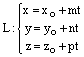 ,
,  ,в которых
,в которых 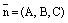 координаты нормального вектора плоскости
координаты нормального вектора плоскости 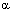 ,
,  – координаты произвольной фиксированной точки прямой L,
– координаты произвольной фиксированной точки прямой L, 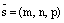 – координаты направляющего вектора прямой L. Тогда:
– координаты направляющего вектора прямой L. Тогда:
1) если  , то прямая L пересекает плоскость
, то прямая L пересекает плоскость 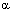 в точке, координаты которой
в точке, координаты которой 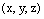 можно найти из системы уравнений
можно найти из системы уравнений
 (7)
(7)
2) если 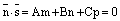 и
и  , то прямая лежит на плоскости;
, то прямая лежит на плоскости;
3) если 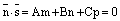 и
и  , то прямая параллельна плоскости.
, то прямая параллельна плоскости.
Доказательство. Условие 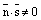 говорит о том, что векторы
говорит о том, что векторы 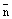 и
и  не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит, пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.
не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит, пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.
Если 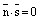 , то это означает, что
, то это означает, что  . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка
. А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка  . Если
. Если  , то точка
, то точка  – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.
– лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.
Если 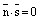 , а
, а  , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости. Теорема доказана.
, то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости. Теорема доказана.
37. Расстояние а) от точки до прямой,
Дано: 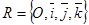 , l:
, l:  , М1(x1, y1, z1).
, М1(x1, y1, z1).
Найти расстояние d (M1, l).
Из уравнений прямой l следует, что точка M0 (x0, y0, z0) лежит на прямой l и вектор 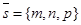 параллелен этой прямой. Искомое расстояние равно высоте параллелограмма, построенного на векторах
параллелен этой прямой. Искомое расстояние равно высоте параллелограмма, построенного на векторах  и
и 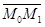 как на сторонах (рис. 37). Следовательно,
как на сторонах (рис. 37). Следовательно,
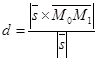 .Переписав это равенство в координатах, получим
.Переписав это равенство в координатах, получим 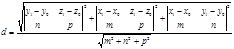 (53)
(53) 
б) между скрещивающимися прямыми.
Дано: 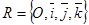 , l1:
, l1: 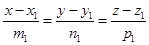 ,l2 :
,l2 :  , l1 и l2 скрещиваются.
, l1 и l2 скрещиваются.
Найти d (l1, l2).
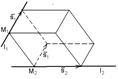
Из уравнений l1 и l2 следует, что M1 (x1, y1, z1) Î l1,M2 (x2, y2, z2)Î l2 и векторы 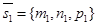 и
и  параллельны прямым l1 и l2 соответственно. Искомое расстояние равно высоте параллелепипеда, построенного на векторах
параллельны прямым l1 и l2 соответственно. Искомое расстояние равно высоте параллелепипеда, построенного на векторах 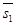 ,
,  и
и 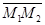 .
.
Следовательно,  .Переписав это равенство в координатах, получим
.Переписав это равенство в координатах, получим
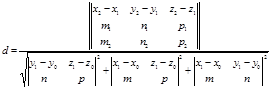 (54)
(54)
Задача 19. Дано: 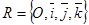 , l1:
, l1:  l2:
l2: 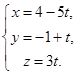
Проверьте, что l1 и l2 скрещиваются и найдите расстояние между ними.
Решение. Найдём направляющий вектор прямой l1 и какую-нибудь точку на ней.
 , М1 = {1, 2, 9}. Из уравнений l2 следует, что
, М1 = {1, 2, 9}. Из уравнений l2 следует, что
М2 (4, -1, 0) и  1, 3}. Вычислим
1, 3}. Вычислим 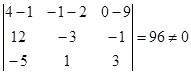 . Следовательно, l1 и l2 скрещиваются. Найдём
. Следовательно, l1 и l2 скрещиваются. Найдём  . Следовательно,
. Следовательно,  =
=  и
и  .
.
38. Угол между а) двумя прямыми,
б) прямой и плоскостью.
Дано: 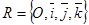 , П: Ах + Ву + Сz + D = 0, t:
, П: Ах + Ву + Сz + D = 0, t:  .
.
Найти один из углов между П и t.
Решение. Угол между прямой и плоскостью – это угол между прямой и её ортогональной проекцией на плоскость. Из уравнений прямой и плоскости вектор 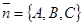 перпендикулярен плоскости П, а вектор
перпендикулярен плоскости П, а вектор  параллелен прямой t. Следовательно,
параллелен прямой t. Следовательно,  ). Отсюда следует, что sin(П,
). Отсюда следует, что sin(П,  =
= 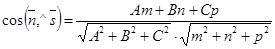 (50)
(50)
Из свойств векторов 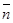 и
и  следует: П // t Û
следует: П // t Û  ; П ^ t Û
; П ^ t Û  (51)
(51)

а)Угол между двумя прямыми в пространстве
За угол между двумя прямыми в пространстве принимают один из двух смежных углов, который образует прямые, проведенные параллельно данным через какую-нибудь точку в пространстве.
Один из этих углов равен углу между направляющими векторами этих прямых.
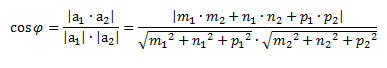
Где первая прямая задается:
 а1=(m1,n1,p1)
а1=(m1,n1,p1)
Вторая прямая задается:
 а2=(m2, n2, p2)
а2=(m2, n2, p2)
Если прямые параллельны, то
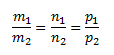
Если прямые перпендикулярны, то m1m2+n1n2+p1p2=0.
39. Геометрический смысл неравенств Ах + Ву + Сz + D £ 0 (< 0, > 0, ³ 0).
Дано: R = 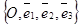 , Ах + Ву + Сz + D ³ 0.
, Ах + Ву + Сz + D ³ 0.
Исследовать, какую фигуру задаёт данное неравенство.
Уравнение Ах + Ву + Сz + D = 0 задаёт плоскость. Пусть это плоскость П. Рассмотрим все точки пространства, не лежащие на П.
Вектор 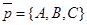 не параллелен плоскости П. Действительно, если бы
не параллелен плоскости П. Действительно, если бы 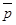 был параллелен П, то А×А + В×В + С×С = А2 + В2 + С2= 0. Но это не возможно. Рассмотрим множество всех точек пространства, не лежащих на плоскости П. Пусть М – любая из этих точек. Проведём через точку М прямую, параллельную вектору
был параллелен П, то А×А + В×В + С×С = А2 + В2 + С2= 0. Но это не возможно. Рассмотрим множество всех точек пространства, не лежащих на плоскости П. Пусть М – любая из этих точек. Проведём через точку М прямую, параллельную вектору  , и пусть она пересекает П в точке N. Векторы
, и пусть она пересекает П в точке N. Векторы  и
и  коллинеарны,
коллинеарны, 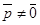 , следовательно,
, следовательно,  . (*) Очевидно, l > 0 Û когда точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор
. (*) Очевидно, l > 0 Û когда точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор  . И l < 0 Û когда точки М лежат в другой открытой полуплоскости с этой же границей. Перейдём к координатам. Пусть М (х, у, z) и N (х1, у1, z1). Тогда
. И l < 0 Û когда точки М лежат в другой открытой полуплоскости с этой же границей. Перейдём к координатам. Пусть М (х, у, z) и N (х1, у1, z1). Тогда 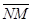 = {x - x1, y - y1, z - z1}. Равенство (*) в координатах перепишется:x - x1 = lA, y - y1 = lB, z - z1 = lC.
= {x - x1, y - y1, z - z1}. Равенство (*) в координатах перепишется:x - x1 = lA, y - y1 = lB, z - z1 = lC.
Отсюда x1 = x - lA, y1 = y - lB, z1 = z - lC. Так как N Î П, то Ах1 + Ву1 + Сz1 + D = 0. Следовательно, А(x - lA) + В(y - lB) + С (z - lC) + D = 0. Ах + Ву + Сz + D = l (A2 + B2 + C2).
Так как A2 + B2 + C2 > 0, то знак Ах + Ву + Сz + D совпадает со знаком l.
Итак, Ах + Ву + Сz + D > 0 Û точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор  . Ах + Ву + Сz + D > 0 Û точки М лежат в другой открытой полуплоскости с этой же границей.
. Ах + Ву + Сz + D > 0 Û точки М лежат в другой открытой полуплоскости с этой же границей.
Неравенства Ах + Ву + Сz + D ³ 0 и Ах + Ву + Сz + D £ 0 определяют замкнутые полуплоскости (их называют просто полуплоскости) с границей П.
Задача 20. Какую фигуру задаёт в аффинной системе координат система 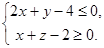 ? Решение. Уравнение x + z - 2 = 0 задаёт плоскость П1, параллельную оси (Оу) и пересекающую оси (Ох) и (Оz) в точках (2, 0, 0) и (0, 0, 2) соответственно. Неравенство
? Решение. Уравнение x + z - 2 = 0 задаёт плоскость П1, параллельную оси (Оу) и пересекающую оси (Ох) и (Оz) в точках (2, 0, 0) и (0, 0, 2) соответственно. Неравенство  задаёт полуплоскость с границей П1, в которой не лежит начало координат (ибо координаты начала координат не удовлетворяют этому неравенству). Уравнение 2x + y - 4 = 0 определяет плоскость П2, параллельную оси (Оz) и пересекающую оси (Ох) и (Оу) в точках (2, 0, 0) и (0, 4, 0). Неравенство
задаёт полуплоскость с границей П1, в которой не лежит начало координат (ибо координаты начала координат не удовлетворяют этому неравенству). Уравнение 2x + y - 4 = 0 определяет плоскость П2, параллельную оси (Оz) и пересекающую оси (Ох) и (Оу) в точках (2, 0, 0) и (0, 4, 0). Неравенство  задаёт полуплоскость с границей П2, в которой не лежит начало координат. Плоскости П1 и П2 пересекаются по прямой АВ. Данная система задаёт пару вертикальных двугранных углов с гранями П1 и П2, ни в одном из которых не лежит начало координат.
задаёт полуплоскость с границей П2, в которой не лежит начало координат. Плоскости П1 и П2 пересекаются по прямой АВ. Данная система задаёт пару вертикальных двугранных углов с гранями П1 и П2, ни в одном из которых не лежит начало координат.


40. Пучки параллельных и пересекающихся плоскостей.
Пучок плоскостей
Если

есть ось пучка, то уравнение пучка

Определение. Пучком плоскостей называется множество всех плоскостей пересекающихся по одной и той же прямой, называемой осью пучка.
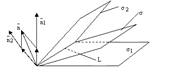
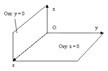
рис.3.
Теорема. Пусть
 и
и 
– две плоскости, пересекающиеся по прямой L. Тогда уравнение
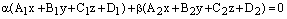 , (10)
, (10)
где 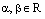 – произвольные действительные числа одновременно не равные нулю, есть уравнение пучка плоскостей с осью пучка L.
– произвольные действительные числа одновременно не равные нулю, есть уравнение пучка плоскостей с осью пучка L.
Пример. Найти уравнение пучка плоскостей, осью которого является ось абсцисс.
Решение. Очевидно, что координатные плоскости
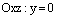 и
и 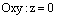 пересекаются по оси Ох.
пересекаются по оси Ох.
Тогда уравнение (10) в данном случае принимает вид 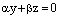 . Заменив греческие буквы на латинские, получаем
. Заменив греческие буквы на латинские, получаем 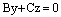 , (11) где
, (11) где 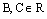 – произвольные действительные числа, одновременно не равные нулю. Уравнение (11) есть искомое уравнение пучка плоскостей с осью пучка Ох.
– произвольные действительные числа, одновременно не равные нулю. Уравнение (11) есть искомое уравнение пучка плоскостей с осью пучка Ох.
Аналогично, уравнение 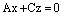 , (12) есть уравнение пучка плоскостей с осью пучка Оу, а уравнение
, (12) есть уравнение пучка плоскостей с осью пучка Оу, а уравнение  (13) есть уравнение пучка плоскостей с осью пучка Оz.
(13) есть уравнение пучка плоскостей с осью пучка Оz.
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 684; Нарушение авторских прав?; Мы поможем в написании вашей работы!