Функция распределения по энергиям

Учитывая определяющую роль энергии, естественно перейти от определения вероятности попадания молекулы в объем 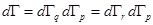к нахождению вероятности для молекулы рассматриваемой системы иметь энергию .

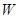Начнем, как мы обычно поступаем, с решения задачи для системы, представляющей собой идеальный газ, т.е. совокупность молекул, взаимодействиями между которыми можно пренебречь.

5.3. Идеальный газ.

В этом случае нет необходимости рассматривать пространственную часть объема фазового пространства 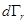, т.к. энергия системы не является функцией координат.

Будем искать вероятность состояния молекулы с энергией, лежащей в интервале от 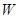до .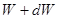

Энергия частицы может быть представлена как 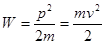. Для определенных значений скорости 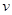, или импульса 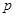, область фазового пространства, соответствующая диапазону энергий 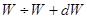, имеет вид тонкого шарового слоя, радиусом .

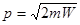Вероятность того, что энергия молекулы принадлежит диапазону значений 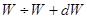, определяется по теореме сложения вероятностей как

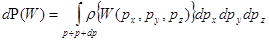, (5.13)

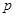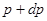где интегрирование ведется по шаровому слою от до . Поскольку рассматриваемый шаровой слой очень тонкий (в его пределах 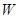практически не меняется), то значение функции распределения 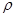внутри него можно считать постоянным, и вынести 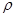из-под знака интеграла:

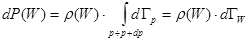(5.14)

Здесь 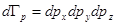, а 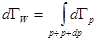- объем шарового слоя с радиусом 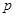. Вычислим его.

Объем шара радиусом 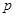находится по хорошо известной формуле

.

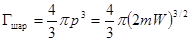Отсюда объем соответствующего шарового слоя:

.

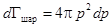Выразим этот объем через энергию:

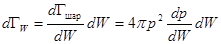, (5.15)

где 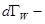число состояний (единичных элементов фазового объема) с энергией между 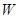и .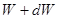

Учитывая, что 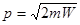, находим из (5.14) и (5.15) для молекулы идеального газа вероятность иметь энергию в интервале значений от 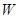до :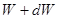

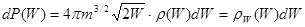, (5.16)

где 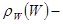новая функция распределения молекул по энергиям:

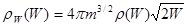. (5.17)

Примечание 1. Важно отличать друг от друга функции распределения, обозначенные 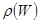и :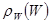

1) функция 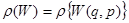определяет плотность вероятности микросостояния (обнаружить систему с заданной энергией 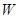в единице фазового объема с координатами 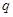и импульсами 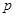), это есть микрораспределение;

2) функция 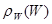представляет собой плотность вероятности обнаружить систему в состоянии с заданной энергией 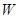при всех возможных значениях координат 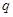и импульсов 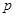, соответствующих этой энергии (шаровой слой в фазовом пространстве), иначе, это есть макрораспределение.

Примечание 2. Если функция микрораспределения 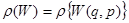определена в пространстве скоростей (т.е. 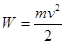), то вероятность иметь энергию в интервале от 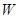до 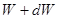для молекулы идеального газа равна

.

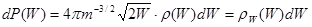5.4. Зависимость функции микрораспределения 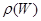от энергии.

Используя вероятностные соображения, можно найти явный вид зависимости функции 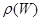от энергии. Выделим в рассматриваемой системе (снова обратимся к идеальному газу) подсистему из двух молекул (невзаимодействующих). Энергия такой подсистемы - аддитивная величина:

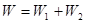. (5.18)

Функция распределения подсистемы по теореме умножения вероятностей равна

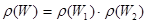, (5.19)

т.е. функция распределения выделенной подсистемы есть не аддитивная величина. Поскольку всегда удобнее работать с аддитивными величинами, можно ввести в рассмотрение логарифм функции распределения по энергиям от энергии:

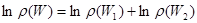, (5.20)

который есть уже величина аддитивная.

Т.о., при описании при описании сложной системы, состоящей из слабовзаимодействующих подсистем должны суммироваться их энергии и логарифмы функций распределения, являющиеся аддитивными величинами. Однако выражения (5.18) и (5.20), описывающие свойства одной и той же системы можно совместить только в том случае, когда логарифм функции распределения 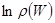является линейной функцией энергии :

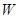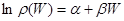, (5.21)

где 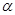и 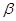- неизвестные пока постоянные.

Итак, общий вид функции распределения 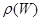имеет вид:

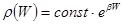. (5.22)

5.5. Произвольная макроскопическая квазизамкнутая подсистема.

Проведем рассуждения, аналогичные приведенным выше, применительно к произвольному макроскопическому телу (неидеальные газы, твердое тело).

Мысленно разбивая систему на квазизамкнутые макроскопические подсистемы, представим полную энергию любой подсистемы как сумму энергий образующих её отдельных частиц (молекул):

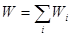, (5.23)

где теперь под 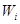мы понимаем как кинетическую, так и потенциальную энергии частиц.

При этом энергия подсистемы есть функция координат и импульсов всех образующих её частиц 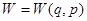, где и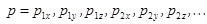

Мы знаем, что вероятность нахождения подсистемы в элементе объема 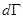многомерного фазового пространства определяется как

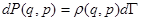(5.24)

Здесь

-

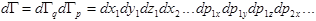дифференциал 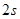(или 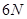) порядка, где 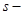число степеней свободы ( 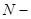число частиц).

Из стационарности функции распределения 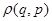следует, что она зависит лишь от интегралов движения, а именно от энергии. Поэтому

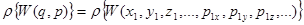(5.25)

Функция 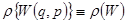– микрораспределение, определяющее нахождение системы в состоянии с заданной энергией при определенных значениях компонент координаты и импульса.

Найдем теперь, как мы это делали для одной молекулы идеального газа, вероятность состояния системы, которое определяется только заданием энергетического интервала 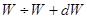при всех возможных значениях компонент координаты и импульса, т.е. перейдем к макрораспределению .

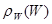Вероятность состояния системы с энергией от 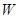до 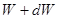определяется как

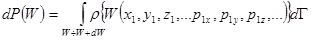. (5.26)

Значениям энергии, заключенным в интервале 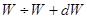, в многомерном фазовом пространстве 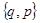соответствует “шаровой слой”, содержащий все множество фазовых (изображающих) точек всех возможных значений компонент обобщенных координат и импульсов, при которых рассматриваемая подсистема обладает энергией от 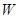до .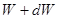

Поскольку рассматривается тонкий “шаровой слой”, то внутри его можно считать функцию 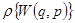постоянной и вынести из-под знака интеграла.

Далее, вводя объем многомерного шарового слоя 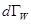как

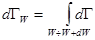, (5.27)

можем записать

.

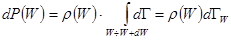Заметим, интеграл (7.27) берется по 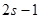(или по 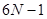) переменным, поэтому 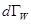- уже дифференциал первого порядка.

Как и в предыдущем параграфе (при рассмотрении идеального газа), свяжем дифференциал 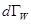с соответствующим приращением энергии 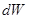и введём функцию макрораспределения 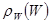подсистемы по энергиям:

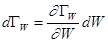. (5.28)

Тогда

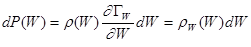, (5.29)

Или

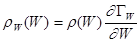. (5.30)

Условие нормировки записывается как

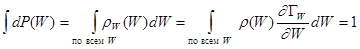. (5.31)

Еще раз отметим существо различия между используемыми функциями микрораспределения 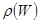и макрораспределения .

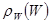Можно сказать, что

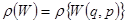- плотность вероятности иметь энергию в интервале от 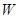до 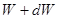системе, находящейся в единице фазового объема,

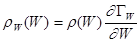- плотность вероятности иметь энергию в интервале от 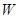до 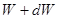системе, находящейся в любой точке всего объема фазового пространства.

(Пример с мишенью).

Прежде, чем приступить к нахождению явного вида функции распределения 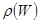для произвольной квазизамкнутой равновесной макроскопической системы, как мы это сделали для идеального газа, определим параметры, используемые при статистическом подходе к описанию таких систем.

5.6. Флуктуации энергии.

Ранее мы установили, важное свойство аддитивных величин, характеризующих поведение макроскопических квазизамкнутых подсистем: их флуктуации в состоянии равновесия малы 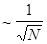, где 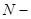число маленьких подсистем (или число частиц). Поэтому средние значение таких величин позволяют описывать состояния системы.

Поскольку статистическое поведение и свойства замкнутой (квазизамкнутой) системы определяются аддитивным интегралом движения – энергией, покажем теперь, что аналогично состояние замкнутой (квазизамкнутой) системы в состоянии равновесия может быть охарактеризовано средним значением её энергии .

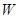Разобьем квазизамкнутую подсистему на множество более мелких одинаковых квазизамкнутых подсистем (каждая из них слабо взаимодействует с окружением). Пусть число таких подсистем N. Тогда энергия подсистемы равна сумме энергий более мелких подсистем:

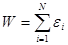. (5.32)

Для оценки средней энергии подсистемы можем принять, что средние энергии 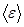малых подсистем одинаковы, поскольку мы разбивали систему на одинаковые малые подсистемы. Тогда

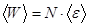. (5.33)

Сосчитаем теперь среднюю квадратичную флуктуацию рассматриваемой подсистемы, воспользовавшись соотношениями (5.32) и (5.33)

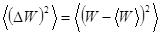
Для упрощения процедуры расчета рассмотрим сначала совокупность двух малых подсистем с энергиям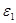и и 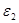, а затем используем полученный результат, распространив его на произвольное число малых подсистем.

.

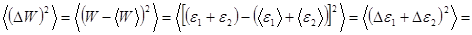
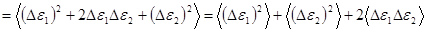В силу квазинезависимости малых подсистем

.

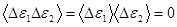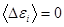, поскольку отклонения энергии малой подсистемы от среднего в стороны меньших и больших значений равновероятны. Тогда получаем

.

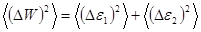Аналогично запишем теперь среднюю квадратичную флуктуацию для разбиения на 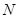малых подсистем.

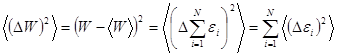. (5.34)

Воспользуемся еще раз тем, что малые подсистемы примерно одинаковы, положив, что флуктуации в них в среднем также имеют одинаковые величины:

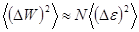(5.35)

Тогда для относительной квадратичной флуктуации получаем:

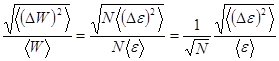. (5.36)

Как видно из этого соотношения, при больших 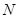относительные флуктуации ничтожно малы. Т.е. как и для

распределения молекул по объему квазизамкнутая система живет

подавляющую часть времени в состоянии с энергией, близкой к средней.

Иначе, энергия равновесной подсистемы 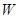практически постоянна во

времени и равна своему среднему значению: .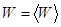

Это означает, что функция распределения имеет резкий пик при

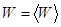и качественную зависимость, изображенную на рисунке.

Заметную величину 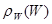имеет только при ничтожно малых

отклонениях 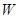от 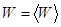; при заметных отклонениях 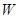от

плотность вероятности становится практически равной нулю:

.

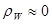Это означает, что любая квазизамкнутая система почти все время проводит в очень небольшой части фазового пространства, соответствующей энергии 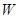вблизи . Эту область можно оценить, исходя из того, что площадь под кривой равна единице (площадь прямоугольника высотой, равной значению 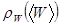в точке максимума, и шириной 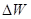на его полувысоте):

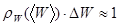, (5.37)

8.2. Фазовый объем и статистический вес.

По порядку величины интервал энергий 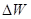, в котором лежат малые допустимые отклонения энергии подсистемы от своего среднего значения, совпадает со средней квадратичной флуктуацией 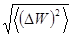, т.е. мал.

Поэтому для оценки объема фазового пространства, в котором рассматриваемая подсистема проводит подавляющую часть времени, можно в функцию распределения по энергиям поставить среднее значение энергии:

,

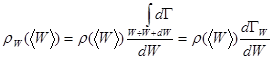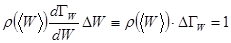, (5.38)

где .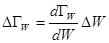

Значение 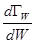характеризует число состояний, приходящихся на единичный энергетический интервал, а 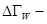та часть фазового пространства, в которой интересующая нас подсистема с энергией проводит почти все время.

Т.о., мы вернулись к фазовому объему “шарового” слоя 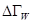(но более толстого – здесь стоит ).

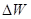Дата добавления: 2015-05-29