Объем несет информацию о полном числе микроскопических состояний подсистемы, которые реализуют макроскопическое состояние равновесной подсистемы с энергией

Ранее мы ввели понятие статистического веса и определили его как число микросостояний реализующих данное макросостояние. При статистическом описании тепловых свойств тел в фазовом пространстве роль статистического веса играет фазовый объем 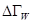. Этот объем тем больше, чем больше число микроскопических реализаций макроскопического состояния подсистемы с энергией .

Естественно попытаться установить связь между статистическим весом, характеризующим макросостояние подсистемы, и объемом 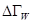фазового пространства.

Статистический вес – величина безразмерная, а фазовый объем 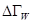– размерная величина (имеет размерность действия – 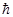). Поэтому определим статистический вес макроскопического состояния 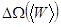как величину, пропорциональную фазовому объему :

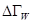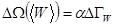(5.39)

где 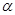- размерный коэффициент пропорциональности.

Если теперь подсистему с энергией разбить на подсистемы меньшего размера, то состояние каждой малой подсистемы будет определяться ее средней энергией 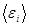. В свою очередь, для каждой малой подсистемы можно определить статистический вес 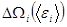ее макросостояния, характеризуемого энергией .

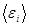Так как малые подсистемы статистически независимы, то энергия рассматриваемой подсистемы определяется как

,

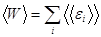а её статистический вес находится по теореме об умножении вероятностей (мультипликативная величина) как

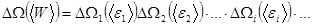, (5.40)

поскольку состояние с энергией рассматриваемой подсистемы реализуется в том случае, когда состояния всех малых подсистем одновременно определяются своими средними значениями энергии.

8.3. Энтропия.

Очевидно, что и в этом случае для характеристики макроскопического состояния подсистемы нам следует воспользоваться аддитивной величиной, а именно: .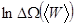

Таким способом в статистической физике вводится э нтропия подсистемы:

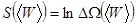. (5.41)

Поскольку число микросостояний, реализующих данное макросостояние, всегда не меньше единицы, то энтропия любой системы (подсистемы) не может быть отрицательной.

Термин энтропия, как мы уже знаем, был введен Клаузиусом и на греческом языке он означает “превращение”.

Дадим следующее статистическое толкование понятию энтропия.

Энтропия, как и фазовый объем 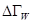, характеризует число микроскопических реализаций термодинамического состояния (макросостояния) подсистемы. Очевидно, что чем большим числом равновероятных способов реализуется термодинамическое состояние, тем чаще подсистема попадает в это макросостояние. Поэтому, согласно принципу Больцмана, вероятность системе оказаться в каком-либо макросостоянии тем больше, чем больше энтропия (статвес) этого состояния.

Число микроскопических реализаций термодинамического состояния растет с увеличением степени беспорядка в подсистеме. Поэтому говорят, что энтропия является мерой степени беспорядка в подсистеме.

Подставляя в уравнение (5.41) выражение (5.39), находим связь между энтропией подсистемы 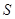и её фазовым объемом :

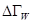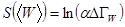. (5.42)

Примечание 1. Поскольку 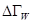– размерная величина,в выражение для энтропии входит постоянная ( 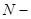число частей подсистемы), т.е. произвольная постоянная. Поэтому энтропия, как в термодинамике, так и в статистике определяется с точностью до произвольной постоянной.

Для любой i -ой подсистемы фазовый объем может быть выражен через её энтропию:

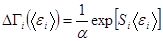. (5.43)

Тогда вероятность нахождения малой подсистемы в макроскопическом состоянии с энергией в интервале вблизи 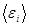пропорциональна

.

Энтропия большой подсистемы, статвес которой равен произведению статистических весов малых подсистем

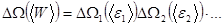, (5.44)

может быть найдена как сумма энтропий малых подсистем:

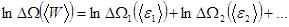, (5.45)

или

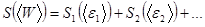(5.46)

Итак, энтропия равновесного тела равна сумме энтропий его малых равновесных частей.

Энтропия - аддитивная величина. А мы знаем, что флуктуации аддитивных величин малы 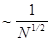, где 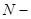число малых равновесных подсистем, составляющих большую подсистему. Следовательно, для энтропии флуктуации также малы .

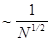Из свойства аддитивности следует, что энтропия, помимо энергии 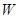, зависит от объема тела 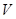, но не зависит от формы тела, т.к. изменение формы тела – это только перестановка его частей, соответствующая перестановке слагаемых в сумме энтропий отдельных малых подсистем. Т.о., получаем для энтропии ту же функциональную зависимость, что и термодинамике:

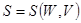, (5.47)

т.е. макроскопическое состояние тела определяется всего двумя параметрами: его энергией 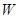и объемом .

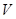Малое изменение макроскопического состояния тела сопровождается малым изменением энтропии 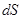, которое определяется суммой:

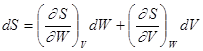, (5.48)

где первое слагаемое – приращение энтропии за счет изменения энергии тела, второе – за счет изменения объема тела.

Примечание 2. Энтропия, определяемая соотношением (5.41)

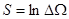
безразмерна. Поэтому абсолютная температура будет иметь размерность энергии

.

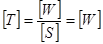Как отмечалось, энергетические (кинетические) единицы температуры являются наиболее естественными, вытекающими из современных представлений о теплоте. Однако в современной физике широко пользуются искусственно построенными шкалами температур. Связь между кинетической и абсолютной термодинамической температурами имеет вид

,

где 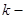постоянная Больцмана.

Чтобы сохранить вид тердинамических соотношений и избежать появления в них постоянной 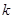, можно, используя произвол в определении энтропии, одновременно с заменой единиц измерения температуры произвести замену .

Тогда энтропия определяется выражением

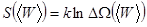
и приобретает размерность постоянной Больцмана.

Дата добавления: 2015-05-29