Принятие решений после построения модели

Интерпретация результатов

Адекватная линейная модель, имеет вид полинома первой степени. Коэффициенты полинома являются частными производными функции отклика по соответствующим переменным. Их геометрический смысл – тангенсы углов наклона гиперплоскости к соответствующей оси. Больший по абсолютной величине коэффициент соответствует большему углу наклона и, следовательно, более существенному изменению параметра оптимизации при изменении данного фактора.

До сих пор мы употребляли абстрактный математи­ческий язык. Перевод модели на язык экспериментатора называется интерпретацией модели.

Задача интерпретации весьма сложна. Ее решают в несколько этапов. Первый этап состоит в следующем. Устанавливается, в какой мере каждый из факторов влияет на параметр оптимизации. Величина коэффициента регрессии – количественная мера этого влияния. Чем больше коэффициент, тем сильнее влияет фактор. О харак­тере влияния факторов говорят знаки коэффициентов. Знак плюс свидетельствует о том, что с увеличением зна­чения фактора растет величина параметра оптимизации, а при знаке минус – убывает. Интерпретация знаков при оптимизации зависит от того, ищем ли мы максимум или минимум функции отклика. Если 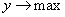, то уве­личение значений всех факторов, коэффициенты которых имеют знак плюс, благоприятно, а имеющих знак минус – неблагоприятно. Если же то, наоборот, благо­приятно увеличение значений тех факторов, знаки коэф­фициентов которых отрицательны.

Далее выясняется, как расположить совокупность факторов в ряд по силе их влияния на параметр оптимиза­ции. Факторы, коэффициенты которых не значимы, конечно не интерпретируются. Можно сказать только, что при данных интервалах варьирования и ошибке воспроиз­водимости они не оказывают существенного влияния на параметр оптимизации.

Изменение интервалов варьирования приводит к изме­нению коэффициентов регрессии. Абсолютные величины коэффициентов регрессии увеличиваются с увеличением интервалов. Инвариантными к изменению интервалов остаются знаки линейных коэффициентов регрессии. Однако и они изменяться на обратные, если при движении но градиенту мы «проскочим» экстремум.

В некоторых задачах представляет интерес построение уравнения регрессии для натуральных значений факто­ров. Уравнение для натуральных переменных можно получить, используя формулу перехода. Коэффи­циенты регрессии изменятся. При этом пропадает воз­можность интерпретации влияния факторов по величинам и знакам коэффициентов регрессии. Вектор-столбцы нату­ральных значений переменных в матрице планирования уже не будут ортогональными, коэффициенты опреде­ляются зависимо друг от друга. Если же поставлена задача получения интерполяционной формулы для нату­ральных переменных, такой прием допустим.

Теперь мы получили основу для перехода к следующему этапу. На основе априорных сведений обычно имеются некоторые представления о характере действия факторов. Источниками таких сведений могут служить теория изучаемого процесса, опыт работы с аналогичными процессами или предварительные опыты и т.д.

Если, например, ожидается, что с ростом температуры должно происходить увеличение параметра оптимизации, а коэффициент регрессии имеет знак минус, то возникает противоречие. Возможны две причины возникновения та­кой ситуации: либо в эксперименте допущена ошибка, и он должен быть подвергнут ревизии, либо неверны априорные представления. Нужно иметь в виду, что экспе­римент проводится в локальной области факторного прост­ранства и коэффициент отражает влияние фактора только в этой области. Заранее неизвестно, в какой мере наивно распространить результат на другие области. Теоретиче­ские же представления имеют обычно более общий характер. Кроме того, априорная информация часто основывается на однофакторных зависимостях. При переходе к многофакторному пространству ситуация может изме­няться. Поэтому мы должны быть уверены, что эксперимент проведен корректно. Тогда для преодоления противо­речия можно выдвигать различные гипотезы и проверять их экспериментально.

В тех, довольно редких, случаях, когда имеется большая априорная информация, позволяющая выдвигать ги­потезы о механизме явлений, можно перейти к следую­щему этапу интерпретации. Он сводится к проверке гипо­тез о механизме явлений и выдвижению новых гипотез.

Получение информации о механизме явлений не яв­ляется обязательным в задачах оптимизации, но возмож­ность такого рода следует использовать. Здесь особое внимание приходится уделять эффектам взаимодействия факторов. Как их интерпретировать?

Пусть в некоторой задаче взаимодействие двух факто­ров значимо и имеет положительный знак. Это свидетель­ствует о том, что одновременное увеличение, как и одновременное уменьшение, значений двух факторов приво­дит к увеличению параметра оптимизации (без учета ли­нейных эффектов).

Интерпретация эффектов взаимодействия не так однозначна, как линейных эффектов. В каждом случае имеется дна варианта. Какому из вариантов отда­вить предпочтение? Прежде всего, нужно учесть знаки линейных эффектов соответствующих факторов. Если эф­фект взаимодействия имеет знак плюс и соответствующие линейные эффекты отрицательны, то выбор однозначен: сочетание –1 и –1. Однако возможен случай, когда знаки линейных эффектов различны. Тогда приходится учи­тывать численные значения коэффициентов и жертво­вать самым малым эффектом.

Иногда приходится учитывать технологические сообра­жения: например, эксперимент в одной области фактор­ного пространства дороже (или труднее), чем в другой.

Упомянем еще об интер­претации эффектов взаимодействия высоких порядков. Если значимым оказался эффект взаимодействия трех факторов, например , то его можно интерпретиро­вать следующим образом. Этот эффект может иметь знак плюс, если отрицательные знаки будут у четного числа факторов (ноль или любые два). Знак минус будет, если нечетное число факторов имеет знак минус (все три или любой один). Это правило распространяется на взаимодействия любых порядков. Пользуются еще таким приемом: произведение двух факторов условно считают одним фактором и сводят трехфакторное взаимодействие к парному и т.д.

Мы сказали, что интерпретация результатов – это перевод с одного языка на другой. Такой перевод обеспечивает взаимопонимание между статистиком и экспериментатором, работающим совместно над задачами оптимизации. Интерпретация уравнения регрессии важна не только для понимания процесса, но и для принятия реше­ний при оптимизации.

Дата добавления: 2015-05-26