Числа подобия

Числам (критериям) подобия присвоены имена уче­ных, сделавших большие открытия в области тепло­обмена и гидродинамики. Такие числа обозначаются одной или двумя начальными буквами фамилий этих ученых.

3.1. Число Нуссельта (Nu)

Это число подобия определяет интенсивность конвек­тивного теплообмена на границе стенка — жидкость. Чем интенсивнее происходит конвективный теплообмен, тем больше число Nu и тем больше коэффициент тепло­отдачи α, что видно из следующей формулы:

Nu = αl₀ /λ, (19.2)

где α — коэффициент теплоотдачи, Вт/(м²- К); λ — тепло­проводность жидкости, Вт/(м-К); ₀ l₀ — определяющий ли­нейный размер, м.

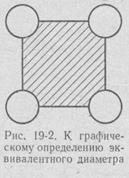
Определяющим называется размер, которым опреде­ляется развитие процесса теплообмена. Если жидкость, участвующая в теплообмене, протекает в круглой трубе, то определяющим размером является d — внутренний диаметр трубы. При поперечном обтекании трубы или пучка труб в уравнение (19.2) подставляется вместо l₀ значение наружного диаметра трубы или труб. Если сечение канала, но которому течет жидкость, слож­ной формы, то определяющим размером является так называе­мый эквивалентный диаметр l₀ = d _экв= 4f/S, где f — площадь поперечного сечения канала; S — смоченный периметр канала. На­пример, если жидкость протекает вдоль труб, расположенных ряда­ми, то f равна заштрихованной площади, как показано на рис. 19-2.

При продольном обтекании плиты определяющим размером является ее длина l, т. е. l₀ = l.

3.2. Число Рейнольдса (Re)

Число подобия Рейнольдса Re определяет характер движения жидкости:

Re = w₀l₀/v, (19.3)

где w₀ — средняя (линейная) скорость жидкости, м/с; определяется отношением объемного расхода к пло­щади сечения потока:

w₀ = V_t/f

(здесь V_t — объемный расход жидкости, м³/с; f — площадь поперечного сечения потока, м²); v — кинема­тическая вязкость жидкости, м²/с, являющаяся одним из свойств жидкости.

Для канала некруглого сечения вместо внутреннего диаметра вводится понятие—эквивалентный диаметр.

Движение жидкости остается ламинарным, пока без­размерное число Рейнольдса меньше 2320 (Re < 2320).

При Re > 10 000режим движения жидкости считается турбулентным. При числах Рейнольдса больше 2320 и меньше 10 0000 — режим переходный от ламинарного к тур­булентному, т. е. по своему характеру неустойчивый.

Поскольку гидродинамическое подобие тоже является необходимым условием подобия процессов конвективного теплообмена, то в подобных процессах число Рейнольдса должно быть одинаковым.

3.3. Число Прандтля (Рг)

Это число определяет физические свойства жидкости:

Pr = v/a, (19.4)

где а — температуропроводность жидкости, м²/с.

В правой части уравнения (19.4) обе величины— параметры состояния, поэтому и само число подобия явля­ется параметром состояния.

Значение числа Рг идеальных газов зависит только от их атомности.

число Рг

Для идеальных газов одноатомных............ 0,67

двухатомных................................................. 0,72

трехатомных.................................................. 0,80

Зависимость числа Рг реальных газов от температуры очень незначительна.

(19.5)

Число Рг капельных жидкостей заметно изменяется только в пределах температур от 0 °С и примерно до 130 °С (с ростом температуры число Рг увеличивается). При температурах выше 130 °С значение числа Рг из­меняется незначительно и его можно принять равным 1. Зависимость Рг от давления становится заметной только при состояниях жидкости, близких к критическому.

3.4. Число Пекле (Ре)

Число Пекле Ре является произведением чисел по­добия Re и Рг:

Ре = Re • Рг = w₀l₀/a. (19.5)

3.5. Число Грасгофа (Gr)

Число подобия Грасгофа Gr определяет соотношение подъемной силы, вызываемой разностью плотностей холодных и нагретых частиц жидкости, и сил молеку­лярного трения. Другими словами, число Gr характери­зует интенсивность свободного движения жидкости:

Gr = βgl₀³Δt/ v² (19.6)

где β — температурный коэффициент объемного расши­рения, К^-1 (для идеальных газов β = 1/273,15 К ^-1); g— ускорение свободного падения, м/с²; Δt — темпера­турный напор — разность между определяющими тем­пературами жидкости и стенки, °С.

Большинство величин, входящих в правые части об­общенных уравнений конвективного теплообмена, за­висят от температуры. Поэтому необходимо, чтобы зна­чения всех этих величин были отнесены к какой-то одной определяющей температуре. Такой температурой может быть температура стенки, обозна­чаемая t_cт, или средняя температура потока жидкости, обозначаемая t_ж или t_п.

В большинстве случаев в качестве определяющей при­нимается температура набегающего потока жидкости (т. е. температура во входном сечении канала) или сред­няя по его длине.

Если отношение температур жидкости при входе в ка­нал t_ж1 и при выходе из него t_ж2 меньше 2, то средняя температура жидкости по длине канала t_ж может опреде­ляться как средняя арифметическая температура:

T_ж,ср =0,5(t_ж1 + t_ж2). (19.7)

(19.8)

При значительной разности температур t_ж1 и t_ж2 в качестве средней температуры жидкости принимается средняя логарифмическая температура:

t_ж =(Δt_вх- Δt_вых)/[2,3lg(Δt_вх/ Δt_вых)] (19.8)

Здесь Δt_вх и Δt_вых — разности температур жидкости и стенки соответственно при входе в канал и при выходе из него.

Таким образом, в уравнении конвективного тепло­обмена может вводиться температура стенки или средняя температура жидкости. Чтобы указать, какая из этих температур принята в данном конкретном случае в ка­честве определяющей, в расчетные уравнения вводится соответствующий индекс («ст» или «ж»). Часто в индексе указывается также, что принимается в данном конкретном уравнении в -качестве определяющего размера: длина l или h — при вертикальной стенке или диаметр d (дейст­вительный или эквивалентный). Поэтому числа подобия могут быть написаны, например, так: Re_{d ж}, Nu_{1 ст}, Nu_h. _ж (или Re_ж, Nu_ст, Nu_ж).

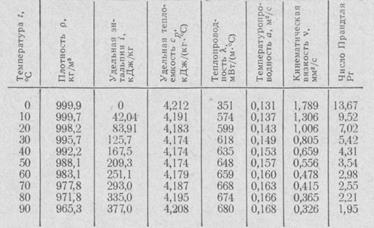
Ниже в табл. 1 и 2 приведены значения величин, входящих в рассмотренные выше числа подобия, а также значения числа Прандтля, отнесенные к температурам, указанным в первой колонке этих таблиц.

Таблица 1

Физические свойства сухого воздуха (при давлении р= 101,325 кПа)

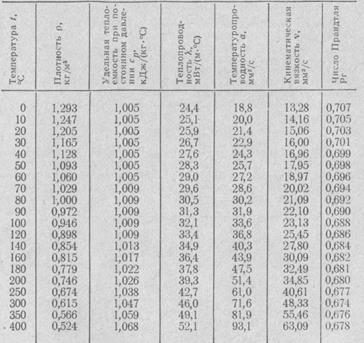
Таблица 2

Физические свойства воды на линии насыщении (при давлении р= 101,325 кПа)

Дата добавления: 2015-05-26