Метод Рунге — Кутта

Метод Эйлера

1. Что является решением дифференциального уравнения?

2. Необходим ли поиск начальных условий в методе Эйлера?

3. К какой группе относится модифицированный метод Эй­лера?

4. Почему точность метода Эйлера пропорциональна h, а мо­дифицированного — h2?

5. Метод Эйлера относится к одно шаговым методам. В чем ос­новное отличие одно- и многошаговых методов?

6. Можно ли методом Эйлера решать системы дифференциаль­ных уравнений?

7. Можно ли использовать метод Эйлера для решения задач, не относящихся к задачам Коши?

8. Обязательно ли необходимо задание начальных условий при решении дифференциального уравнения методом Эйлера?

9. В чем заключается отличие явных и неявных вычислитель­ных схем в модифицированном методе Эйлера?

10. Можно ли оценить погрешность решения дифференциально­го уравнения, не зная точного решения?

1. Сколько раз необходимо на каждом шаге вычислять правую часть уравнения при использовании метода четвертого по­рядка?

2. Как можно оценить погрешность решения дифференциаль­ного уравнения при использовании метода Рунге — Кутта?

3. Можно ли задавать погрешность решения при автоматиче­ском подборе шага в относительных величинах?

4. Сколько предыдущих значений функции нужно иметь, чтобы сосчитать одно следующее значение?

5. К какой группе методов (аналитические или численные) от­носится имеющий аналитическое выражение от искомого значения функции метод Рунге — Кутта?

6. Как записывается рекуррентная формула метода четвертого порядка?

7. Что можно отнести к недостаткам метода, например, самого распространенного четвертого порядка?

8. Как зависит погрешность метода от величины шага решения?

9. Возможно ли применение переменного шага в методе Рунге — Кутта?

Варианты заданий к лабораторной работе

№ п/п	Уравнение	Начальные значение	Конечное значение	Шаг	Начальное значение функции Y
1.	Y' = y + e^2x		1,5	0.16	Y(0)=3
2.	Y' = cos(x) - y			0.2	Y(0)=1.5
3.	Y' =	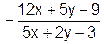		0,2	Y(0)=0
4.	Y' = x^2 -	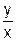		0,2	Y(1)=1
5.	Y' = e^2x - 3y			0,2	Y(0) = 0
6.	Y' =	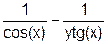		0,2	Y (0) = 2
7.	Y' = e^x – x + 2y			0,2	Y (0) = 0
8.	Y' =	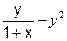		0,2	Y (0) = 1
9.	Y' =	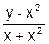		0,2	Y (1)=1
10.	Y' = -4y + sin(2x)			0,2	Y(0) = 1
11.	Y' = -y + e^-xcos(x)			0,1	Y(0) = 0
12.	Y' = -y + 1-e^x			0,2	Y(0) = 2,5
13.	Y' = -y + e^xcos(x)			0,2	Y(0) = 0
14.	Y' = -y – sin(xe^x)			0,1	Y(0) = 1
15.	Y' = xy			0,2	Y(0) = 1
16.	Y' = x+	1,7		0,1	Y0(1,7) = 5,3
17.	Y' =	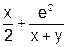1,8	2,5	0,15	Y0(1,3) = 4,5
18.	Y' =	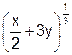3,1	5,4	0,1	Y0(3) = 5
19.	Y' =	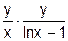	1,5	0,3	Y0(1) = О,5
20.	Y' = 2x + sin	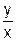0,1		0,05	Y0(0,1)=1
21.	Y' =	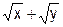		0,1	Y0(0) = 0
22.	Y' =	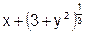		0,1	Y0(0) = 0
23.	Y' =	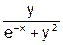0,1		0,1	Y0(0,1)=1
24.	Y' = x-y			0,1	Y0(0) = 0
25.	Y' =	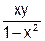	0,5	0,1	Y0(0,1)=1
26.	Y' = 2xy			0,05	Y0(0) = 1
27.	Y' = 2x – 3y			0,05	Y0(0) = 1

ЛАБОРАТОРНАЯ РАБОТА № 5
Символьные переменные

Цель работы

Ознакомление с принципами программирования задач с символьными переменным.

Дата добавления: 2015-05-29