Цилиндрическая стенка

Очень часто теплоносители движутся по трубам, и требуется рассчитать тепловой поток, передаваемый через цилиндрическую стенку трубы. Задача о распространении теплоты в цилиндрической стенке при известных и постоянных температурах на внутренней и наружной поверхностях, также одномерная, если ее рассматри­вать в цилиндрических координатах. Температура изменяется только вдоль радиуса (по координате r ), а по длине трубы и по ее периметру остается не­изменной. В этом случае dt/drи закон Фурье будет иметь вид

q = -λ(dt/dr) (8.14)

или для трубы длиной l

Q =Fq =-2πr/λ dt/dr (8.15)

Интегрировать удобно уравнение (8.15), так как тепловой поток не меняет­ся по толщине стенки, а q = Q/F ≠ const, поскольку площадь F = 2πrl, через кото­рую проходит тепловой поток, зависит от радиуса.

Разделим переменные: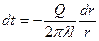

(8.16)

Интеграл этого уравнения (8.16)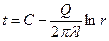

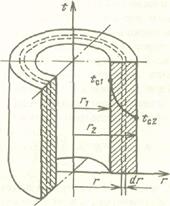
Рис. 21 Изменение температуры по толщине однослойной цилиндрической стенки

У внутренней поверхности, где кривизна стенки больше, температура меняется резче, чем у наружной.

Интегрирование уравнения (8.16) в определенных пределах (по tот t_c1до t_c2и по r от r₁до г₂) дает зависимость для расчета теплового потока через ци­линдрическую стенку:

Q =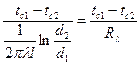

Для труб обычно измеряется и при­водится в условиях задач диаметр, а не радиус, поэтому отношение радиусов r₂/r₁ заменено отношением диаметров

d₂/d₁ Термическое сопротивление для ци­линдрической стенки имеет вид

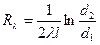(8.19)

причем при d₂/d₁≈ 1 расчет должен про­водиться с высокой точностью, поскольку небольшая погрешность, допущенная при определении отношения d₂/d₁, в этом случае дает значительную ошибку при вычислении логарифма.

Для определения теплового потока через многослойную цилиндрическую стенку следует, как и для многослойной плоской стенки, просуммировать терми­ческие сопротивления отдельных слоев:

Q = 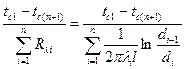(8.20)

Отличие формулы (8.20) от (8.12) заключается только в способе расчета термических сопротивлений отдельных слоев для плоской и цилиндрической сте­нок. Но и это различие существенно только при больших отношениях наруж­ного и внутреннего диаметров каждого слоя d_н/d_вн = d_i+1/d_i > 1,5. При мень­ших отношениях d_н/d_вн термические со­противления отдельных слоев, как уже было показано, целесообразнее считать по упрощенной формуле 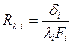справедливой для плоской стенки.

Расчет температур на границах слоев в данном случае осуществляется так же, как для многослойной плоской стенки, т. е. по формуле (8.13).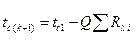

Шаровая стенка. При постоянных температурах t_c1 t_c2 на внутренней (ра­диусом r₁) и наружной (радиусом r₂)поверхностях шаровой стенки темпера­турное поле одномерно в сферических координатах, т. е. температура изменяет­ся только по радиусу. Следовательно, Q = qF = - λF(dt/dr) = -λ4πr²(dt/dr) (8.21)

Разделив переменные и проинтегри­ровав по (в пределах от t_c1 и t_c2 по rв пределах от r₁ до r₂: (8.22)

получим расчетную формулу для тепло­вого потока через шаровую стенку:

Q =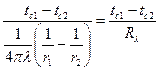

Дата добавления: 2015-05-26