Уравнение теплопроводности

Для вывода уравнения теплопроводности используем уравнение теплового баланса, которое является следствием закона сохранения энергии и констатирует:

Разность между притоками тепла выделенного объема и оттоком тепла из выделенного объема, равняется измененного количества тепла в этом объеме.

Изменение количества тепла

Отток тепла

Приток тепла

За время dt в стержень через левую грань поступает количество тепла

R q(x) · S ·dt (1)

За это время через правую грань уходит количество тепла

q(x + dx) · S · dt (2)

В (1) и (2): q – плотность потока тепла [q] – Дж/м²·с; S – площадь сечения стержня [S] – м²

[q· S·dt] = Дж/м²·с ·м²·с = Дж

Пусть q = 5Дж/м²·с

Согласно уравнению теплового баланса:

[q(x) – q(x + dx)]·S·dt = dQ (3)

Здесь dQ – изменение количества тепла в стержне за время dt/

dQ = m· C_ν ·dT = ρ ·dx ·S · C_ν·dT (4)

В (4) m = ρ · dx ·S

m – масса участка стержня длины dx,

С_ν – удельная теплоемкость

[dQ] = кг/м³·м·м²·Дж/ кг·К = Дж

По определению производной функции в левой части (3)

q = (x + dx) – q(x) =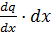

Тогда из (3) и (4) следует:

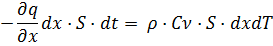
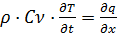(5)

Плотность теплового потока определяется по закону Фурье

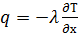(6)

Тогда из (5) имеем

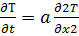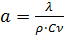; (7)

(7) уравнение молекулярной теплопроводности; a – коэффициент температуропроводности.

[C] = Дж/ кг·К для воды при нормальных условия с = 4200 Дж/кг·К (при изменении температуру 1кг воды на 1˚,необходимо 4200Дж количества тепла)

Если температуру необходимо повысить на 1˚, то нужно сообщить воде 4200 Дж тепла; а если температуру необходимо понизить на 1˚, то нужно отнять 4200 Дж тепла.

Разные вещества и среды имеют разное значение теплоемкости, которое зависит от внутренней структуры вещества.

В общем случае перенос тепла происходит в трехмерном пространстве и границы теплопроводности имеют вид:

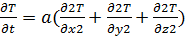(8)

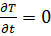стационарный случай.

Оператор (∆) Лапласа:

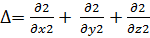(9)

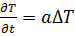
В(8) – оператор Лапласа в декартовой системе координат.

При необходимости оператора Лапласа можно написать в цилиндрической и в сферической системах координат, (8) или (9) – дифференцированные уравнения в частных производных II порядка – уравнения параболического типа.

Их решения позволяют найти поле температуры в рассматриваемой области в любой момент времени Т = Т(x, y, z, t)

Дата добавления: 2015-05-26