
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Тейлора
|
|
|
|
Упражнения для самостоятельной работы
Определить значения следующих выражений:
1.  2.
2.  3.
3. 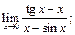
4.  5.
5. 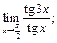 6.
6. 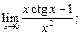
7. 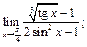 8.
8. 
9. 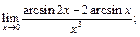 10.
10. 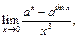
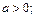
11. 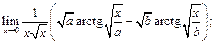 12.
12. 
13. 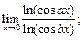 14.
14.  15.
15. 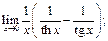
16.  17.
17. 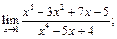 18.
18. 
19.  20.
20. 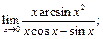
21.  22.
22. 
23. 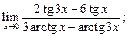 24.
24. 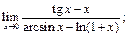
25. 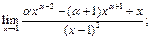 26.
26. 

27. 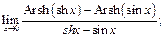 28.
28. 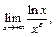
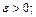
29. 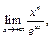
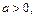
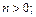 30.
30.  31.
31. 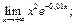
32. 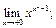 33.
33. 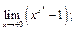 34.
34. 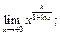 35.
35. 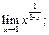
36.  37.
37. 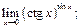 38.
38. 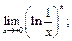
39. 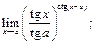 40.
40.  41.
41. 
42. 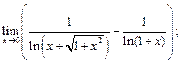 43.
43. 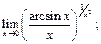
44.  45.
45. 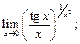 46.
46. 
47. 

48. 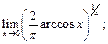 49.
49. 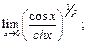
50.  51.
51. 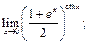 52.
52. 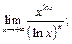
53. 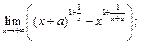
54. 
55.  56.
56. 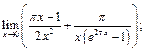
57. 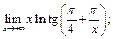 58.
58. 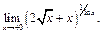
59. Показать, что следующие пределы не могут быть вычислены по правилу Лопиталя, и найти эти пределы:
1)  ; 2)
; 2) 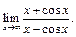
60. Исследовать возможность применения правила Лопиталя к следующему пределу:  .
.
Локальная формула Тейлора или формула Тейлора с остаточным членом в форме Пеано.
Пусть функция 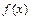 , определённая в окрестности точки
, определённая в окрестности точки  , имеет в этой окрестности производные до
, имеет в этой окрестности производные до  -го порядка включительно, а в точке
-го порядка включительно, а в точке  существует
существует 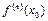 . Тогда справедливо следующее представление:
. Тогда справедливо следующее представление:
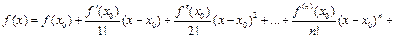
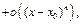

Многочлен  называется многочленом Тейлора функции
называется многочленом Тейлора функции 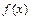 в точке
в точке  , а функция
, а функция  -
- 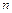 -тым остаточным членом.
-тым остаточным членом.
Формула Тейлора на промежутке.
Если на отрезке с концами  и
и 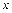 функция
функция 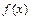 непрерывна вместе со своими производными до
непрерывна вместе со своими производными до 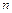 -го порядка включительно, а во внутренних точках она имеет
-го порядка включительно, а во внутренних точках она имеет 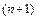 -ю производную, то какова бы ни была функция
-ю производную, то какова бы ни была функция 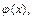 непрерывная на данном отрезке и имеющая отличную от нуля производную в его внутренних точках, найдётся точка
непрерывная на данном отрезке и имеющая отличную от нуля производную в его внутренних точках, найдётся точка 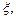 лежащая между
лежащая между  и
и 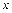 и такая, что
и такая, что
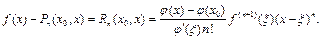
Если при выполненных условиях теоремы
1) 
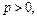
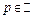 - произвольно, то остаточный член в формуле Тейлора представим в виде Шлемильха-Роша:
- произвольно, то остаточный член в формуле Тейлора представим в виде Шлемильха-Роша:

2)  то остаточный член в формуле Тейлора представим в форме Лагранжа:
то остаточный член в формуле Тейлора представим в форме Лагранжа:
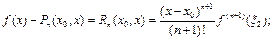
3) 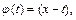 то остаточный член в формуле Тейлора представим в форме Коши:
то остаточный член в формуле Тейлора представим в форме Коши:

Если 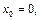 то формула Тейлора принимает вид:
то формула Тейлора принимает вид:
 и называется формулой Маклорена.
и называется формулой Маклорена.
Справедливы пять важных разложений:
1. 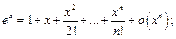
2. 
3. 
4. 
5. 
В примерах 1-14 разложить функцию 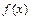 по формуле Маклорена до
по формуле Маклорена до 
Пример 1. 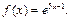
Пользуясь разложением 1, получим:

Пример 2. 
Так как 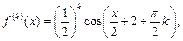 т.е.
т.е. 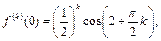 то разложение по формуле Тейлора будет иметь следующий вид:
то разложение по формуле Тейлора будет иметь следующий вид:

Пример 3. 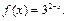
Учитывая, что 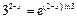 и используя разложение 1, получим:
и используя разложение 1, получим:
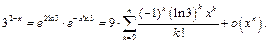
Пример 4. 
Так как 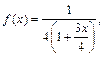 то с использованием разложения 5 будем иметь:
то с использованием разложения 5 будем иметь:

Пример 5. 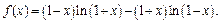
Из разложения 4 следует: 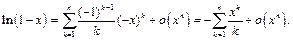
Поэтому 
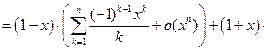
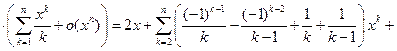
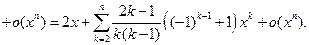
Пример 6. 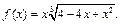
Преобразовав подкоренное выражение, используем затем разложение 5:
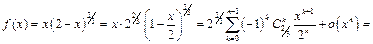
 где
где

Пример 7. 
После преобразований применим разложение 4:
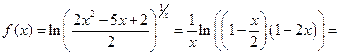
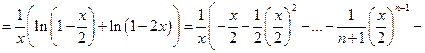
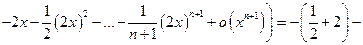

Учитывая, что 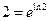 и
и 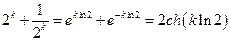 , будем иметь:
, будем иметь:
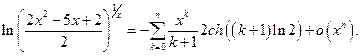
Пример 8. 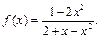
Разделив числитель на знаменатель, представим 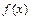 в виде:
в виде:
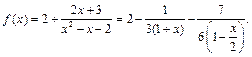
Тогда 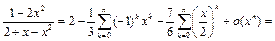
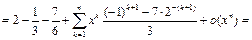
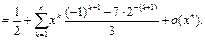
Пример 9. 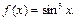
Так как 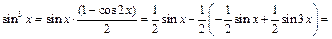
 то используя разложение 2, будем иметь:
то используя разложение 2, будем иметь:
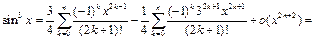

Пример 10. 
Учитывая, что  а
а
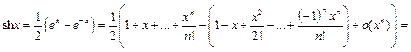
 получим:
получим:
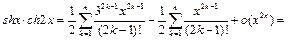
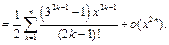
Пример 11. 
Используя формулу 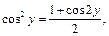 преобразуем функцию:
преобразуем функцию: 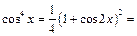
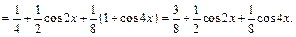
Применяя разложение 3, будем иметь:
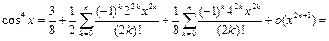
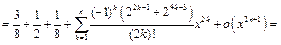
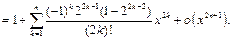
Пример 12. 
Преобразуя функцию с помощью формул понижения степени 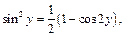
 получим:
получим: 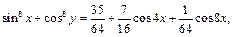 откуда с использованием разложения 3 будем иметь:
откуда с использованием разложения 3 будем иметь:
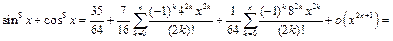
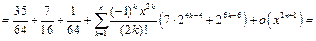
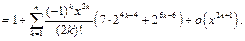
Пример 13. 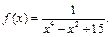
Представим 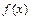 в виде суммы дробей:
в виде суммы дробей:
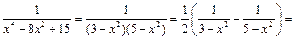
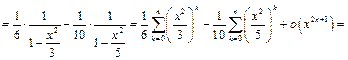

Пример 14. 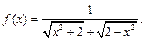
Преобразуем функцию: 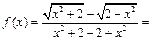
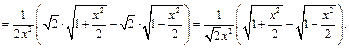
Воспользуемся разложением 5, введя для краткости следующее общепринятое обозначение:

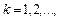
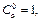 тогда
тогда  Следовательно,
Следовательно,
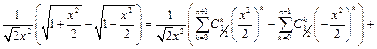
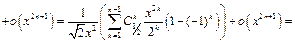
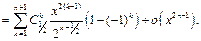 Заменяя переменную
Заменяя переменную  окончательно получим:
окончательно получим: 
Если функция 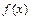 имеет вид:
имеет вид:  и известны разложения функций
и известны разложения функций 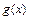 и
и  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  до
до 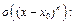

 причём
причём 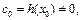 то для нахождения разложения функции
то для нахождения разложения функции 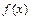 применим метод неопределённых коэффициентов. Пусть искомое разложение имеет вид:
применим метод неопределённых коэффициентов. Пусть искомое разложение имеет вид:
 тогда, так как
тогда, так как 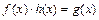 или
или
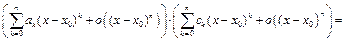
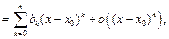 то приравнивая в последнем равенстве коэффициенты при одинаковых степенях
то приравнивая в последнем равенстве коэффициенты при одинаковых степенях  в правой и левой частях, получим систему алгебраических уравнений для определения
в правой и левой частях, получим систему алгебраических уравнений для определения 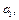

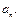
Пример 15. Применяя метод неопределённых коэффициентов, разложить по формуле Маклорена функцию  до
до 
Учитывая, что функция  нечётная и
нечётная и 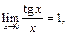 т.е.
т.е.  будем иметь:
будем иметь: 
Применяя разложения 2 и 3 и формулу 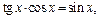 получим:
получим:
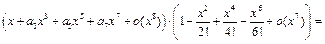
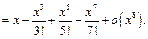 Приравнивая коэффициенты при
Приравнивая коэффициенты при 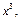
 и
и  находим:
находим:
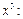
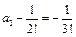

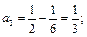

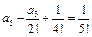


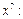
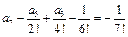


Итак, 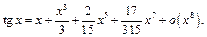
Если  - сложная функция и известны разложения функций
- сложная функция и известны разложения функций 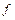 и
и 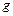 по формуле Тейлора:
по формуле Тейлора:

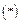
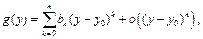

то для нахождения коэффициентов разложения
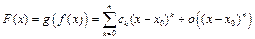
нужно в формулу  подставить
подставить 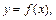 заменить её разложением
заменить её разложением 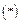 и произвести арифметические действия, сохраняя лишь члены вида
и произвести арифметические действия, сохраняя лишь члены вида 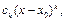 где
где 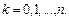
Пример 16.  Разложить по формуле Маклорена до
Разложить по формуле Маклорена до  функцию
функцию 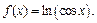
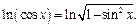 Используя разложения 2 и 4, получим:
Используя разложения 2 и 4, получим:
 Для
Для  имеем:
имеем: 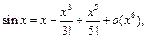 поэтому, оставляя лишь члены вида
поэтому, оставляя лишь члены вида 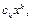
 , будем иметь:
, будем иметь:
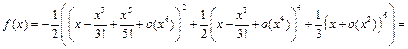
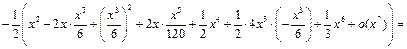
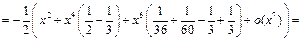
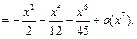
Если требуется разложить функцию 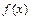 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 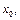 то, сделав замену
то, сделав замену 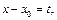 мы получим функцию
мы получим функцию 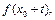 которую необходимо разложить по формуле Маклорена.
которую необходимо разложить по формуле Маклорена.
Пример 17. Разложить по формуле Тейлора в окрестности точки  функцию
функцию  до
до 
Пусть 
 тогда
тогда  и
и 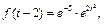
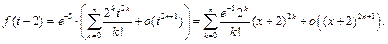
Пример 18. Разложить по формуле Тейлора в окрестности точки  функцию
функцию  до
до 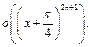
Пусть 
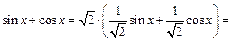
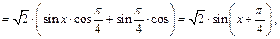 тогда
тогда
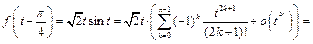
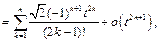 откуда следует:
откуда следует:
 Пример 19. Разложить по формуле Тейлора в окрестности точки
Пример 19. Разложить по формуле Тейлора в окрестности точки 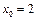 до
до 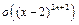 функцию
функцию 
Обозначим 
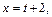 тогда
тогда 
и 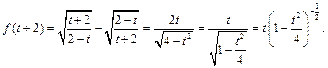
Используя разложение 5, получим:
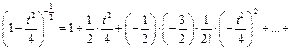
 , откуда
, откуда
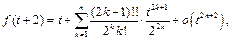
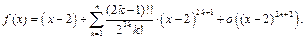
Если известно разложение по формуле Тейлора в окрестности точки  до
до  производной
производной 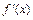 функции
функции 
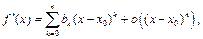 где
где  то существует
то существует 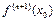 и функцию
и функцию 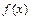 можно представить в виде:
можно представить в виде:

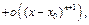 где
где 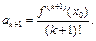 Но
Но 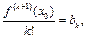 поэтому
поэтому 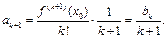 Следовательно,
Следовательно,
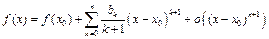 ,
, 
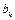 - коэффициенты разложения по формуле Тейлора для функции
- коэффициенты разложения по формуле Тейлора для функции 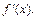
Пример 20. Разложить по формуле Маклорена до 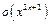 функций: 1)
функций: 1)  2)
2) 
3) 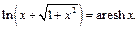
1)  и используя разложение 5, получим:
и используя разложение 5, получим:
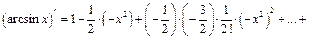


Согласно формуле  будем иметь:
будем иметь:

2)  (легко получить с использованием формулы для геометрической прогрессии). Тогда по формуле
(легко получить с использованием формулы для геометрической прогрессии). Тогда по формуле  можно записать:
можно записать:
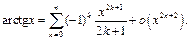
3) 
откуда по формуле  находим:
находим:

Пример 21. Разложить по формуле Маклорена до 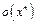 функцию
функцию 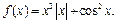 Число
Число 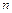 выбрать наибольшим.
выбрать наибольшим.
Рассмотрим функцию 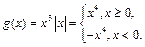
Найдём её производные. При 
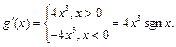 При
При  по определению производной находим:
по определению производной находим:
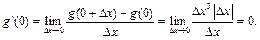
Таким образом, первая производная существует при всех  причём
причём 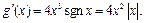 Аналогично для второй производной получаем:
Аналогично для второй производной получаем: 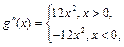
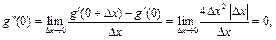 т.е. вторая производная существует при всех
т.е. вторая производная существует при всех 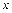 и равна
и равна  Для третьей производной имеем:
Для третьей производной имеем:
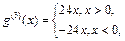
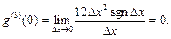 Следовательно,
Следовательно, 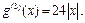 Так как функция
Так как функция 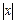 не дифференцируема в точке
не дифференцируема в точке  то рассматриваемая функция
то рассматриваемая функция  не имеет в точке
не имеет в точке  четвёртой производной (и производных порядка выше четвёртого), а обладает в этой точке производными до третьего порядка включительно. Поэтому разложение по формуле Маклорена до
четвёртой производной (и производных порядка выше четвёртого), а обладает в этой точке производными до третьего порядка включительно. Поэтому разложение по формуле Маклорена до  при
при 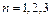 выглядит следующим образом:
выглядит следующим образом:
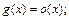

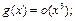 а разложение
а разложение 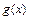 по формуле Маклорена до
по формуле Маклорена до 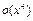 не существует. Итак,
не существует. Итак, 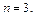
Возвращаясь к функции 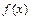 и используя разложение 2 для
и используя разложение 2 для 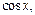 будем иметь:
будем иметь:
 поэтому
поэтому 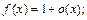
 так как
так как
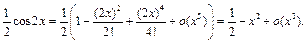
Пример 22. Оценить с помощью формулы Тейлора абсолютную погрешность приближённой формулы:

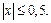
По формуле Тейлора с остаточным членом в форме Лагранжа:
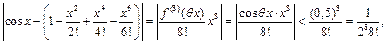
где 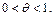
Пример 23. Написать многочлен Тейлора порядка 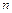 и оценить разность этого многочлена и функции на указанном отрезке, принимая в качестве
и оценить разность этого многочлена и функции на указанном отрезке, принимая в качестве  середину этого отрезка:
середину этого отрезка:  на
на 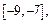

По условию  Находим производные функции:
Находим производные функции:
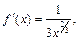
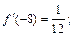
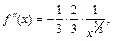
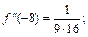
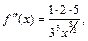
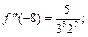
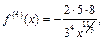

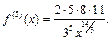
Многочлен Тейлора 4-го порядка функции  для
для  имеет вид:
имеет вид:
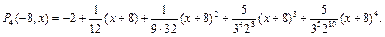
Оценим величину остаточного члена, записанного в форме Лагранжа:
 так как
так как
 на
на 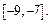
Отметим, что отношения эквивалентности не всегда позволяют выделить главную часть функции при 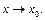 В этом случае одним из методов выделения главной части является разложение функции по формуле Тейлора с остаточным членом в форме Пеано.
В этом случае одним из методов выделения главной части является разложение функции по формуле Тейлора с остаточным членом в форме Пеано.
Пример 24. Найти главную часть функции 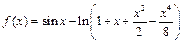 при
при 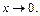
Разложение функции  по формуле Тейлора содержит лишь нечётные степени
по формуле Тейлора содержит лишь нечётные степени  поэтому для функции
поэтому для функции  будем записывать разложение до 1-го, 3-го, 5-го и т.д. порядков включительно, используя при этом известное разложение 4:
будем записывать разложение до 1-го, 3-го, 5-го и т.д. порядков включительно, используя при этом известное разложение 4:
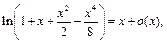


 Тогда
Тогда
 Итак, степенная функция
Итак, степенная функция 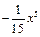 есть главная часть данной функции при
есть главная часть данной функции при 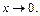
Пример 25. Определить главный член вида  при
при 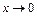 , если
, если 
В примере 15 получено: 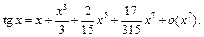 Будем использовать также разложение 2. Данная функция нечётна, поэтому в её разложении по формуле Маклорена будут присутствовать лишь нечётные степени
Будем использовать также разложение 2. Данная функция нечётна, поэтому в её разложении по формуле Маклорена будут присутствовать лишь нечётные степени 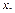 Запишем последовательно многочлены Тейлора функции
Запишем последовательно многочлены Тейлора функции 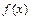 в нулевой точке увеличивающегося порядка, пока не получим многочлен, отличный от нуля.
в нулевой точке увеличивающегося порядка, пока не получим многочлен, отличный от нуля.
Для первого порядка:

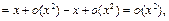
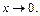
Для третьего порядка:

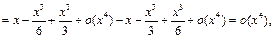
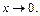
Для пятого порядка:
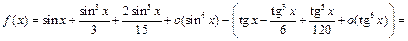
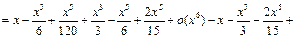
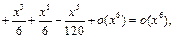
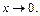
Для седьмого порядка:


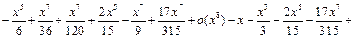

Итак, степенная функция 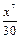 есть главная часть функции
есть главная часть функции 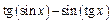 при
при 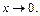
Метод выделения главной части с помощью формулы Тейлора может быть использован и при нахождении пределов.
Пример 26. Найти 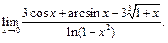
Так как  то числитель дроби следует разложить до
то числитель дроби следует разложить до 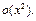 Используя разложения 3, 5 и пример 20, получим:
Используя разложения 3, 5 и пример 20, получим:
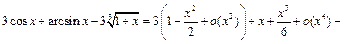
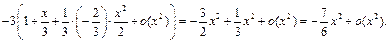
Тогда 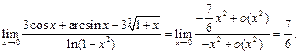
Пример 27. Найти 
Так как 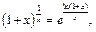 то будем использовать разложения 1 и 4:
то будем использовать разложения 1 и 4:
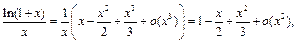
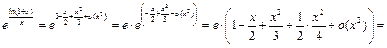
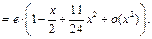
Тогда 
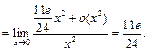
Пример 28. Найти 
Будем использовать разложения 2 и 3:
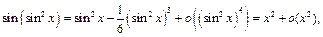
следовательно, и числитель необходимо разложить до
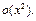

 Тогда
Тогда

Пример 29. Найти 
Для представления знаменателя используем разложения 2, 4, 5:

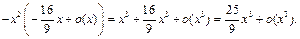
Разложение числителя осуществим до 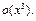 С использованием примеров 10, 15, 20 получим:
С использованием примеров 10, 15, 20 получим:
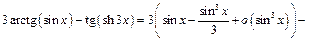
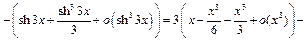
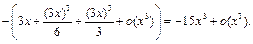
Тогда

Пример 30. Найти 
Так как 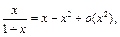 то
то
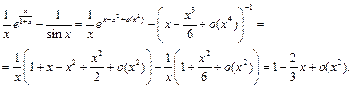
 Тогда
Тогда

Пример 31. Найти 
Используем пример 20 (3) и разложение 2:
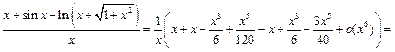
 Тогда
Тогда

Пример 32. Найти 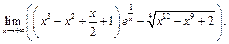
Так как 
 то
то
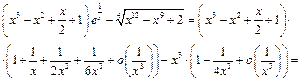


Таким образом,
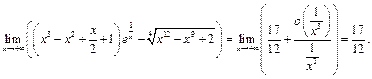
Пример 33. Найти 
Преобразуем разность и воспользуемся примером 20:
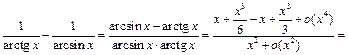
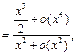 откуда следует, что
откуда следует, что
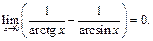
Пример 34. Найти 
Так как 

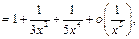 то
то


следовательно,
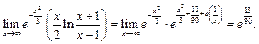
|
|
|
|
|
Дата добавления: 2015-05-31; Просмотров: 1344; Нарушение авторских прав?; Мы поможем в написании вашей работы!