
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упражнения для самостоятельной работы
|
|
|
|
1. Разложить по формуле Маклорена до  функции:
функции:
1) 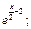 2)
2) 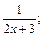 3)
3) 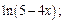 4)
4) 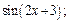
5) 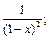 6)
6) 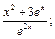 7)
7) 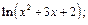
8) 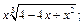 9)
9) 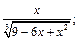 10)
10) 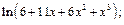
11) 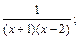 12)
12) 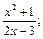 13)
13) 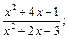
14) 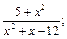 15)
15) 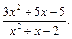
2. Разложить по формуле Маклорена до 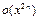 функции:
функции:
1) 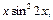 2)
2) 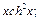 3)
3)  4)
4) 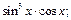
5) 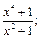 6)
6) 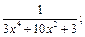 7)
7) 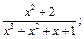
8) 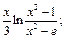 9)
9) 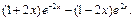
3. Разложить по формуле Маклорена до 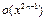 функции:
функции:
1) 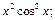 2)
2) 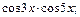 3)
3) 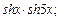 4)
4) 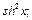
5) 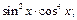 6)
6)  7)
7) 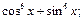
8) 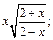 9)
9) 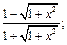 10)
10) 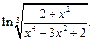
4. Написать разложения по целым неотрицательным степеням переменной 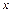 до членов указанного порядка включительно следующих функции:
до членов указанного порядка включительно следующих функции:
1) 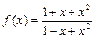 до
до 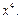 Чему равно
Чему равно 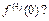
2) 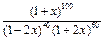 до
до 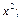 3)
3) 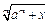
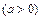 до
до 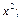
4) 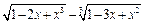 до
до 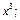 5)
5) 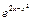 до
до 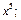
6) 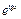 до
до 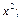 7)
7)  до
до 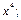 8)
8) 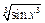 до
до 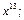
9) 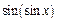 до
до 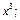 10)
10) 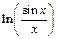 до
до 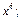
11) 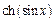 до
до 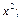 12)
12) 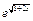 до
до 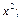
13) 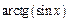 до
до 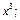 14)
14) 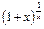 до
до 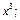
15) 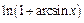 до
до 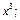 16)
16) 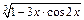 до
до 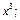
17) 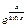 до
до 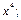 18)
18) 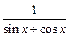 до
до 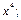
19) 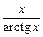 до
до 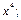 20)
20) 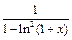 до
до 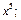
21) 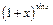 до
до 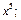 22)
22) 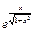 до
до 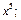
23) 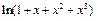 до
до 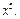
5. Разложить по формуле Тейлора в окрестности точки
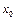 до
до 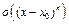 функции:
функции:
1) 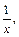
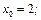 2)
2) 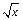 ,
, 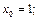 3)
3) 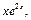
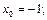
4) 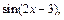
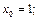 5)
5) 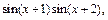
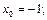
6) 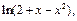
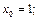 7)
7) 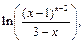
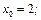
8) 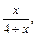
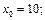 9)
9) 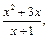
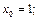 10)
10) 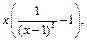
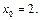
6. Разложить по формуле Тейлора в окрестности точки 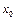 до
до 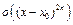 функции:
функции:
1) 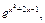
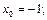 2)
2) 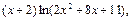

3) 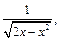
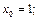 4)
4) 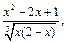
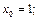
5) 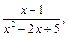
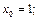 6)
6) 
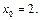
7. Разложить по формуле Тейлора в окрестности точки 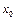 до
до 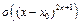 функции:
функции:
1) 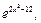
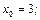 2)
2) 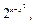
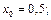 3)
3) 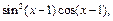
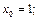
4) 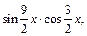
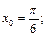 5)
5) 
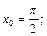
6) 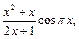
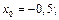 7)
7) 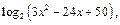
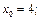
8) 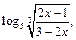
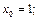 9)
9) 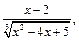
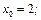
10) 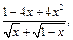
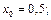 11)
11) 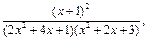
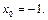
8. Разложить по формуле Маклорена до  функции:
функции:
1) 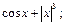 2)
2) 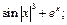 3)
3) 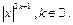 Число
Число 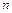 выбрать наибольшим.
выбрать наибольшим.
9. Функцию 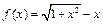
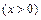 разложить по целым неотрицательным степеням дроби
разложить по целым неотрицательным степеням дроби  до члена с
до члена с 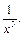
10. Оценить с помощью формулы Тейлора абсолютную погрешность приближённых формул:
1) 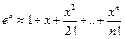 при
при 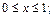
2) 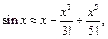
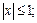 3)
3) 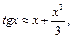
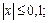
4) 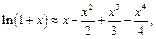
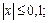
5) 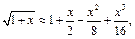
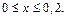
11. Написать многочлен Тейлора порядка 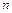 и оценить разность этого многочлена и функции на указанном отрезке, принимая в качестве
и оценить разность этого многочлена и функции на указанном отрезке, принимая в качестве 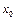 середину этого отрезка:
середину этого отрезка:
1) 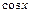 на
на 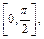
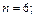 2)
2) 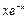 на
на 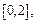
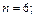
3) 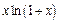 на
на 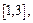
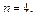
12. Найти такие числа 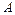 и
и 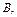 чтобы при
чтобы при 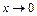 были справедливы асимптотические равенства:
были справедливы асимптотические равенства:
1) 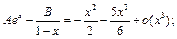
2) 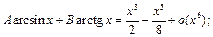
3) 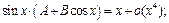
4) 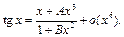
13. Для бесконечно малой при 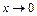 величины
величины 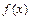 определить главный член вида
определить главный член вида 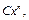 если:
если:
1) 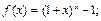 2)
2) 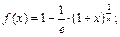
3) 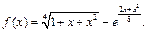
14. Найти пределы:
1) 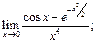 2)
2) 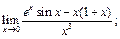
3) 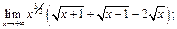 4)
4) 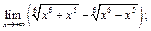
5)  6)
6) 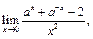
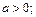
7) 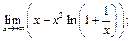 8)
8) 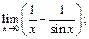
9) 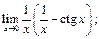 10)
10) 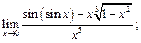
11) 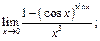 12)
12) 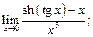
13) 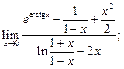 14)
14) 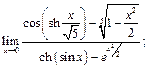
15) 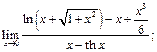
16) 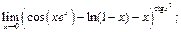
17) 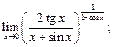 18)
18) 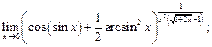
19) 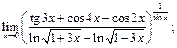 20)
20) 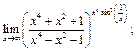
21) 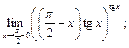 22)
22) 
23) 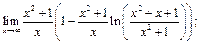
24) 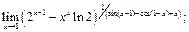
25) 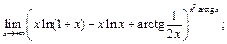
26) 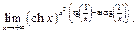
|
|
|
|
|
Дата добавления: 2015-05-31; Просмотров: 335; Нарушение авторских прав?; Мы поможем в написании вашей работы!