Малые равнообъемные наклонения. Теорема Эйлера

Общее понятие об остойчивости

МОДУЛЬ 5. ОСТОЙЧИВОСТЬ. ОСТОЙЧИВОСИТЬ НА МАЛЫХ УГЛАХ НАКЛОНЕНИЙ

Остойчивость - способность судна, выведенного из положения равновесия внешним воздействием, возвращаться в положение равновесия после прекращения этого воздействия. Судно, обладающее такой способностью, является остойчивым, а не обладающее - неостойчивым.

Внешние моменты, наклоняющие судно, совершают работу, которую должна уравновесить работа восстанавливающих сил, т. е. мы должны рассматривать не только статическую остойчивость, но и динамическую. Динамическая остойчивость характеризуется величиной работы восстанавливающего момента, а статическая –величиной самого восстанавливающего момента.

Если на судно действует пара сил, вертикальных перемещений не будет, а возникнут только наклонения (крен или дифферент), которые называются равнообъемными, так как не будет наблюдаться изменение водоизмещения. Ватерлинии, соответствующие равнообъемным наклонениям, называются равнообъемными.

Рассмотрим вначале крен судна (рис. 1) на бесконечно малый угол δθ. Так как 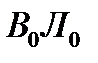и 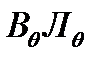- равнообъемные ватерлинии, входящий объем и выходящий объем равны между собой

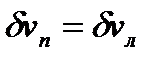. (1)

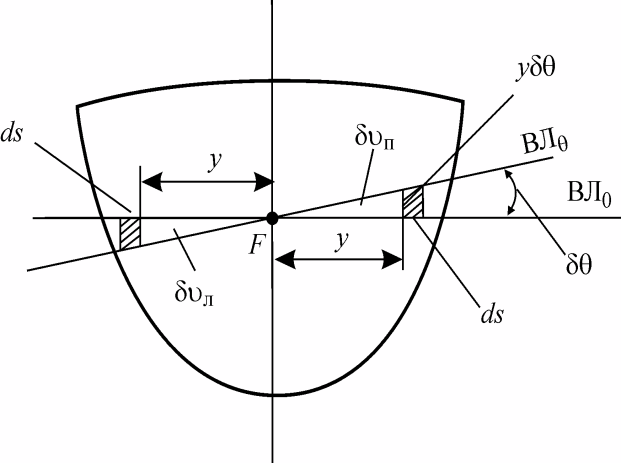
Рис.1. Определение объемов 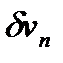и

Объемы 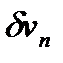и можно определить как суммы элементарных призм с высотой yδθ и основанием ds:

;

, (2)

где s_п - площадь правой части ватерлинии; s_л - площадь левой части ватерлинии.

Если учесть, что - статический момент правой полуплощади ватерлинии относительно оси наклонения, параллельной оси Ох, а 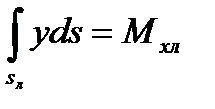- статический момент левой полуплощади, можно подставить (2) в (1) и получить

, (3)

где М_х – статический момент площади всей ватерлинии относительно оси наклонения.

Но, так как левый и правый объемы равны друг другу, М_х = 0.Это возможно только в том случае, если ось, относительно которой вычислен момент М_х, проходит через центр тяжести площади ватерлинии.

Повторив эти же рассуждения для 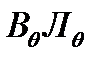, получим, что линия пересечения двух равнообъемных ватерлиний при бесконечно малом наклонении должна проходить через центры тяжести обеих ватерлиний. Это условие называется теоремой Эйлера. Теорема Эйлера верна для любого бесконечно малого наклонения (крена, дифферента).

Следствие из теоремы Эйлера.

Если повернуть плавающее судно на бесконечно малый угол относительно оси, проходящей через центр тяжести площади ватерлинии, то объем погруженной части судна не изменится.

Теорему Эйлера можно распространить и на конечные, но малые углы наклонения. Предельная величина таких углов зависит от формы конкретного судна и от его загрузки. На практике считают углы малыми до 5 – 7 градусов. Для полностью погруженных судов теорема Эйлера справедлива вообще при любых углах наклонения.

Дата добавления: 2015-06-04