
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ответ. 0
|
|
|
|
Задача 18. В атомной физике изучается формула Релея —Джинса, дающая зависимость распределения энергии излучения от частоты:
u  = А —
= А —  . Считая
. Считая  малой величиной, упростить формулу способом линеаризации, считая d
малой величиной, упростить формулу способом линеаризации, считая d  постоянной величиной.
постоянной величиной.
Решение. Если v мало, то  = 1, т.е.
= 1, т.е. 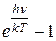 ~
~  или
или 
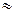 1 +
1 +  , тогда u
, тогда u 
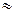 A
A  .
.
Задача 19. Имеется с  грамм-молекул активного вещества. Предполагая, что в единицу времени вступает в реакцию р% этого вещества, узнать, какое количество грамм-молекул не вступит в реакцию по истечении времени t.
грамм-молекул активного вещества. Предполагая, что в единицу времени вступает в реакцию р% этого вещества, узнать, какое количество грамм-молекул не вступит в реакцию по истечении времени t.
Решение. Через единицу времени вступают в реакцию 0,01рс  грамм-молекул; остаются с
грамм-молекул; остаются с  (1 —
(1 — 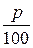 ). Через 2 единицы времени не вступило в реакцию с
). Через 2 единицы времени не вступило в реакцию с  (1 —
(1 — 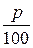 )
) 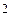 . Через t единиц времени количество грамм-молекул с
. Через t единиц времени количество грамм-молекул с  (1 —
(1 — 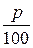 )
) 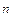 . Для лучшего приближения к действительности единицу времени разобьем на n более мелких частей. Тогда вещества, не вступившего в реакцию, будет с
. Для лучшего приближения к действительности единицу времени разобьем на n более мелких частей. Тогда вещества, не вступившего в реакцию, будет с  (1 —
(1 — 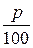 )
)  , или, полагая
, или, полагая 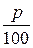 = k, получим
= k, получим
(1 – k) 
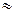 1 - kt
1 - kt 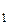 = 1 – kt/n, тогда вещества, не вступившего в реакцию, будет с
= 1 – kt/n, тогда вещества, не вступившего в реакцию, будет с  (1 — kt/n)
(1 — kt/n) 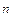 .
.
Истинное количество остающегося вещества
с = 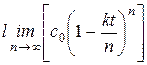 = c
= c  e
e 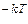 .
.
Задача 20. Упростить барометрическую формулу
h = 800 (1 + 0,004t) 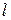 n
n  , принимая
, принимая  =
= 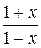 ,
,
где 0  x
x  1.
1.
Ответ. h =  .
.
Задача 21. В топографии возникает необходимость найти отношение стрелы f = DB (высоты сегмента) дуги ABC окружности радиуса r к стреле f 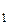 = D
= D 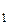 B
B 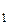 половины АВ
половины АВ  В этой дуги, если центральный угол АОВ мал. Найти это отношение.
В этой дуги, если центральный угол АОВ мал. Найти это отношение.
Указание. Построить центральные углы дуг и использовать принцип эквивалентности бесконечно малых.
Ответ.  4.
4.
Задача 22. «В педагогическом эксперименте сравниваются результаты по двум различным методикам обучения. Материал темы излагается в двух группах, где применялись единые тестовые задания. В качестве переменной выступает безразмерная величина х = t/Т (0 <t < Т), где T - общее количество часов для изучения темы.
Средние коэффициенты усвоения темы, в зависимости от степени «погружения» в теоретический материал, для каждой группы выражаются функциями  .
.
Как выяснить эффективность предложенных методик?»
Этап анализа позволяет сделать вывод о том, что для данных зависимостей требуется сравнить значения Р  (1) и Р
(1) и Р  (1), которые непосредственно из формул определить нельзя.
(1), которые непосредственно из формул определить нельзя.
На этапе классификации выясняется, что каждая функция является комбинацией конечного числа элементарных, поэтому для 0 < х < 1 функции непрерывные.
Этап расчленения целого на части дает возможность выявить, что для установления результата к концу обучения следует найти пределы указанных функций при х  1, сравнив значения между собой. Надо сказать, что понятие предела, сложное по своей природе, приобретает здесь вполне конкретные очертания.
1, сравнив значения между собой. Надо сказать, что понятие предела, сложное по своей природе, приобретает здесь вполне конкретные очертания.
На этапе установления и определения последовательностей возникает проблема вычисления предела сложной функции. В первом случае аргумент является бесконечно большой величиной, а во втором — представляет собой «неопределенность вида 0/0 «.
Использование теоремы о предельном переходе под знаком непрерывной функции завершается на этапе определения взаимосвязей.
На этапе синтеза сравниваются два предельных значения Р  (1) = 1/2, Р
(1) = 1/2, Р  (1) = Ln 2 и делаются выводы.
(1) = Ln 2 и делаются выводы.
Задача 23. Задача предложена в учебнике Б.В.Гнеденко и отмечено, что ее сюжет заимствован из звездной астрономии. "В сфере радиуса R случайно и независимо друг от друга разбросано n точек. Чему равна вероятность того, что расстояние от центра сферы до ближайшей точки будет не менее r, если r < R?" Решая эту задачу, студенты получают ответ р = 1-(1 - 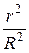 )
) 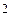 . Можно предложить выяснить, к чему будет стремиться полученная вероятность (и объяснить полученный ответ) при следующих условиях:
. Можно предложить выяснить, к чему будет стремиться полученная вероятность (и объяснить полученный ответ) при следующих условиях:
1) n, r фиксированы, R 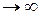 ;
;
2) n, R фиксированы, r  R;
R;
3) n, R фиксированы, r  0;
0;
4) n, R фиксированы, r 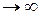 ;
;
5) n, R 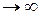 , причем
, причем 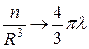 .
.
Условия, сформулированные в пункте 5, предложены в учебнике, причем отмечено, что в звездной астрономии в окрестности Солнца 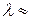 0,0063, если R измерено в парсеках.
0,0063, если R измерено в парсеках.
24. В расчетной практике по абсорбции, дистилляции, экстракции и выщелачиванию встречается функция f(х) =  .
.
Найти предел этой функции при х 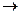 1.
1.
ХИМИЧЕСКИЕ СПЕЦИАЛЬНОСТИ
Раздел 1. Введение в анализ
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 676; Нарушение авторских прав?; Мы поможем в написании вашей работы!