
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные оптические формулы. Построение изображения
|
|
|
|
На рис. 3.4.1 даны кардинальные точки – главные точки  ; фокусы
; фокусы 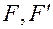 - оптической системы. Требуется построить изображение предмета
- оптической системы. Требуется построить изображение предмета  .
.
Для нахождения изображения точки  проследим ход двух лучей. Один луч направим параллельно оптической оси (
проследим ход двух лучей. Один луч направим параллельно оптической оси ( ), сопряженный луч пройдет через задний фокус
), сопряженный луч пройдет через задний фокус  системы и через точку
системы и через точку 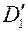 . Второй луч проведем через передний фокус
. Второй луч проведем через передний фокус 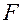 системы. Сопряженный луч в пространстве изображений идет параллельно оптической оси. Построенные в пространстве изображений лучи
системы. Сопряженный луч в пространстве изображений идет параллельно оптической оси. Построенные в пространстве изображений лучи  и
и  пересекаются в точке
пересекаются в точке 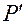 , которая и является изображением точки
, которая и является изображением точки  .
.
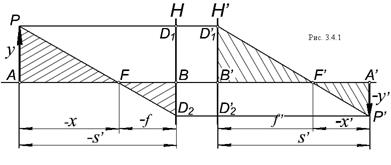 Пользуясь подобием одинаково заштрихованных треугольников
Пользуясь подобием одинаково заштрихованных треугольников 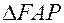 и
и  и
и 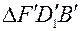 , найдем:
, найдем:
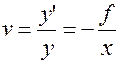 ,
, 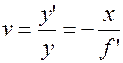 .
.
Это две расчетные формулы для линейного увеличения. Приравнивая правые части формул, получим формулу, известную под названием - формула Ньютона:

Введем отрезки  и
и  . По рисунку видим:
. По рисунку видим:
 ,
, 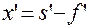
Подставляя в формулу Ньютона, получим:
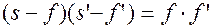 ;
; 
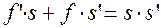
Деля на 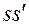 , найдем формулу отрезков:
, найдем формулу отрезков:
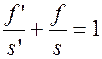 ,
,
при  (система находится в однородной среде):
(система находится в однородной среде):
 .
. 
Из фомул:

 ;
; 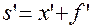 ;
; 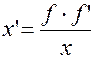 (формула Ньютона)
(формула Ньютона)
имеем:
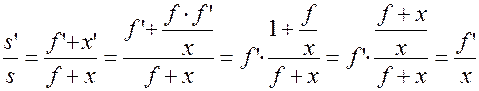
Из формулы Ньютона:
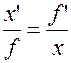
Таким образом
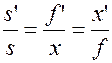
Это выражение позволяет получить формулу для линейного увеличения через отрезки s и s’
 ;
; 
При  формула приобретает простой вид
формула приобретает простой вид
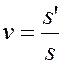
Рассмотрим графическое построение изображения. При построении изображения мы исходим из свойств лучей, проходящих через кардинальные точки системы. Проследив ход двух лучей, исходящих из какой-либо точки предмета, и прошедших через оптическую систему, мы находим их точку пересечения в пространстве изображений, которая и будет искомым изображением точки предмета. Следует иметь в виду, что пространство предметов не обязательно находится слева от системы, а пространство изображений – справа: они могут находиться с любой стороны.
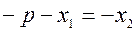 ;
; 
 ;
; 
По формуле Ньютона:
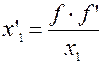 ;
; 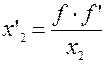
Тогда

и

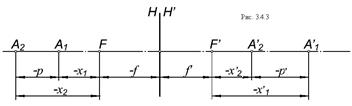 Обозначив линейное увеличение в точках
Обозначив линейное увеличение в точках 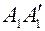 через
через  , а в точках
, а в точках 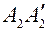 через
через 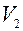 , можно записать:
, можно записать:

В случае, когда точка  неограниченно приближается к точке
неограниченно приближается к точке 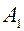 , то
, то 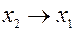 и
и  . В пределе, когда точка
. В пределе, когда точка  совпадает с точкой
совпадает с точкой 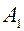 , продольное увеличение
, продольное увеличение 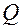 переходит в продольное увеличение в точках, обозначаемое через
переходит в продольное увеличение в точках, обозначаемое через  ,
,

Если  , то
, то 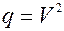 .
.
 Мы знаем, что угловое увеличение
Мы знаем, что угловое увеличение 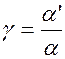 (рис. 3.4.4).
(рис. 3.4.4).
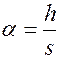 ;
; 
Тогда

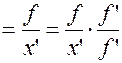
Но
 ;
; 
Тогда 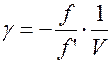 ;
; 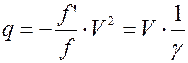
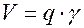 ,
,
то есть линейное увеличение равно произведению углового увеличения на продольное.
Инвариант Аббе
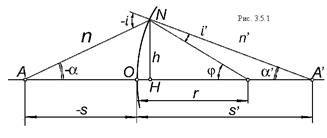
Пусть две среды с показателями преломления 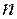 и
и 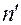 разделены преломляющей поверхностью с радиусом кривизны
разделены преломляющей поверхностью с радиусом кривизны  (рис. 3.5.1).
(рис. 3.5.1).
По закону преломления:

При малых углах  и
и  можно записать:
можно записать:
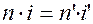
Проведем произвольный луч 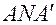 . Так как углы
. Так как углы  и
и  малы, то будет мала величина
малы, то будет мала величина 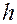 . Пренебрегая отрезком
. Пренебрегая отрезком 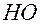 , можно записать из треугольников
, можно записать из треугольников 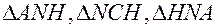 :
:
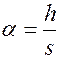 ;
;  ;
;  .
.
Из треугольника 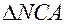 ,
,  - внешний угол,
- внешний угол,
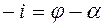 ;
; 
Из треугольника 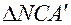 ,
, 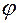 - внешний угол,
- внешний угол,
 ;
; 
Подставляя в уравнение закона преломления, получаем:

или
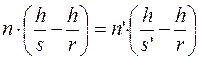
Сокращая на  , получаем инвариант Аббе:
, получаем инвариант Аббе:

Из формулы Аббе следует, что положение точки 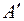 зависит только от положения точки
зависит только от положения точки  и не зависит от углов, образованных лучом с осью. То есть, всякий луч, проходящий через точку
и не зависит от углов, образованных лучом с осью. То есть, всякий луч, проходящий через точку  непременно пройдет через точку
непременно пройдет через точку 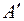 .
.
Однако эта формула справедлива только для параксиальных лучей, идущих бесконечно близко к оптической оси. Для лучей образующих конечные углы с оптической осью, так называемых действительных лучей, мы не можем делать замену закона преломления, которая осуществлена нами в начале параграфа. Следовательно, положение точки 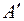 будет зависеть от угла
будет зависеть от угла  и гомоцентрический пучок лучей исходящий из точки
и гомоцентрический пучок лучей исходящий из точки  перестает быть гомоцентрическим при сходе в точке
перестает быть гомоцентрическим при сходе в точке 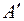 . Изображение
. Изображение 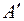 точки
точки  становится размытым.
становится размытым.
Формула Аббе позволяет найти фокусные расстояния одной преломляющей поверхности. Для этого примем, что луч идет из бесконечности, то есть  , тогда
, тогда  :
:
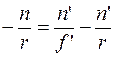 ;
; 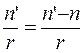 ;
; 
И наоборот 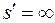 , тогда
, тогда  .
.
 ;
; 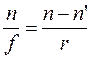 ;
; 
Определим отношение фокусных расстояний
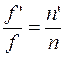
При 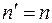 :
:  .
.
Из рис. 3.5.2 видно

 ;
;  .
.
Также:
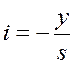 ;
;  .
.
Подставляя эти формулы в закон преломления для малых углов, получим:
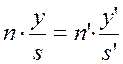 ;
; 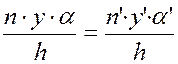 ;
; 
Это так называемая формула или инвариант Лагранжа-Гельмгольца.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 3487; Нарушение авторских прав?; Мы поможем в написании вашей работы!